- Captured On
- Source
- Nonlinear Systems | Unit IV: First-order Systems | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is an autonomous system?
1.1 Front
What is an autonomous system?
General First Order Autonomous Systems
1.2 Back
The word autonomous means self regulating. These systems are self regulating in the sense that their rate of change (e.g. derivatives) depends only on the state of the system (values of \(x\) and \(y\)) and not on the time \(t\)
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
This is the standard form of a first-order autonomous system
2 Which form does solutions of a first-order autonomous system have?
2.1 Front
Which form does solutions of a first-order autonomous system have?
2.2 Back
\({\displaystyle \vb{x}(t) = \begin{pmatrix}x(t) \\ y(t)\end{pmatrix}}\)
3 How is the velocity field of this linear system?
3.1 Front
How is the velocity field of this linear system?
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
3.2 Back
The solution has the form \({\displaystyle \vb{x} = \begin{pmatrix}x(t) \\ y(t)\end{pmatrix}}\), which velocity field is \(\dot{\vb{x}}\)
\({\displaystyle \dot{\vb{x}} = \begin{pmatrix}x’(t) \\ y’(t)\end{pmatrix}}\)
For each point \((x_0, y_0)\) on the \(xy\text{-plane}\) has a velocity vector having its tail at \((x_0, y_0)\):
\({\displaystyle \dot{\vb{x}} = \begin{pmatrix}f(x_0, y_0) \\ g(x_0, y_0)\end{pmatrix}}\)
So, it is represented geometrically as a vector field
4 What is a critical point for this linear system?
4.1 Front
What is a critical point for this linear system?
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
4.2 Back
This is a first-order autonomous system which has its critical points if \(f(x_0,y_0) = 0\) and \(g(x_0,y_0) = 0\)
It’s also called stationary points
In this case, it’s velocity vector is zero, so \(x = x_0\) and \(y = y_0\) is a constant solution to the linear system
It’s the simplest possible solution
5 What is a stationary point in an autonomous linear system?
5.1 Front
What is a stationary point in an autonomous linear system?
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
5.2 Back
It’s the same as critical points. These points are a trajectory all by itself, since by not moving it satisfies the equation of the linear system.
6 What is the sketching principle for linear system?
6.1 Front
What is the sketching principle for linear system?
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
6.2 Back
Assuming that these functions are smooth, (it’s continuously differentiable), then two trajectories of this linear system cannot intersect
7 How could we solve this autonomous linear system?
7.1 Front
How could we solve this autonomous linear system?
- \({\displaystyle x’ = f(x,y)}\)
- \({\displaystyle y’ = g(x,y)}\)
7.2 Back
We can eliminate \(t\) from the system by dividing one equation by the other. Since by the chain rule
\({\displaystyle \frac{y’}{x’} = \frac{\dv{y}{t}}{\dv{x}{t}} = \dv{y}{x}}\)
We get after the division a single first-order ODE in \(x\) and \(y\)
\({\displaystyle \begin{matrix}x’ & = & f(x,y) \\ y’ & = & g(x,y)\end{matrix} \qquad \rightarrow \qquad \dv{y}{x} = \frac{g(x,y)}{f(x,y)}}\)
If the first order equation on the right is solvable, this is an important way of getting information about the solutions of the system on the left.
8 What are the differences between First Order Autonomous ODE system and First Order ODE’s
8.1 Front
What are the differences between First Order Autonomous ODE system and First Order ODE’s
\({\displaystyle \begin{matrix}x’ & = & f(x,y) \\ y’ & = & g(x,y)\end{matrix} \qquad \rightarrow \qquad \dv{y}{x} = \frac{g(x,y)}{f(x,y)}}\)
How are their solutions?. What do they differentiate each other?
8.2 Back
The system involves time, whereas the single ODE does not. Consider how their solutions are related
\({\displaystyle \begin{matrix}x & = & x(t) \\ y & = & y(t)\end{matrix} \qquad \rightarrow \qquad F(x,y) =0 }\)
where the equation on the right is the result of elimininating \(t\) from the pair of the equation on the left.
Geometrically, \(F(x,y) = 0\) is the equation for the trajectory of the solution \(\vb{x}(t)\) on the left. It doesn’t contain any record of how fast the point was moving. It’s only the track (or trace) of its motion
9 What are the differences between First Order Autonomous ODE system and First Order ODE’s?
9.1 Front
What are the differences between First Order Autonomous ODE system and First Order ODE’s?
\({\displaystyle \begin{matrix}x’ & = & f(x,y) \\ y’ & = & g(x,y)\end{matrix} \qquad \rightarrow \qquad \dv{y}{x} = \frac{g(x,y)}{f(x,y)}}\)
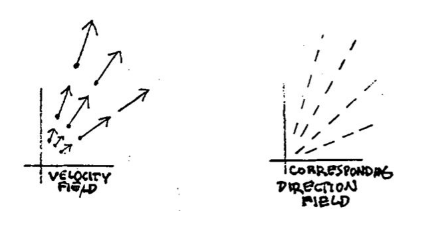
What differences are there between velocity field and direction field?
9.2 Back
The velocity vectors have magnitude and sense, whereas the line segments that make up the direction field only have slope.
The passage from the left side to the right side is represented geometrically by changing each of the velocity vectors to a line segment of standard length. Even the arrowhead is dropped, since it represents the direction of increasing time, and time has been eliminated; only slope of the vector is retained