- Captured On
- Source
- Qualitative Behavior: Phase Portraits | Unit IV: First-order Systems | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is the phase plane for this system?
1.1 Front
What is the phase plane for this system?
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
1.2 Back
It’s the \(xy\text{-plane}\) itself, where you can draw the trajectory of a solution with an arrow to indicate the direction of increasing time.
2 What is a phase portrait?
2.1 Front
What is a phase portrait?
2.2 Back
It is the graphs of enough trajectories in the phase plane to give a good sense of all solutions to the system
3 What is a critical point for this system?
3.1 Front
What is a critical point for this system?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
3.2 Back
The point \((x_0, y_0)\) is a critical point of the system if
\({\displaystyle \begin{pmatrix}\dot{x} \\ \dot{y}\end{pmatrix} = A \begin{pmatrix}x_0 \\ y_0\end{pmatrix} = \begin{pmatrix}0 \\ 0\end{pmatrix}}\)
The equations of the system show this is equivalent to
- \(x = x_0\)
- \(y = y_0\)
is a constant solution to the system
4 Why are important the critical points for this system?
4.1 Front
Why are important the critical points for this system?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
4.2 Back
Critical points are the key to our qualitative view of systems. We classify the linear systems by their behavior near critical points.
5 Which is the critical point that have all systems?
5.1 Front
Which is the critical point that have all systems?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
5.2 Back
The point \((0,0)\)
6 When can we say that the system only has the point 0 as critical point?
6.1 Front
When can we say that the system only has the point 0 as critical point?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
6.2 Back
If the matrix \(A\) is invertible, then \((0,0)\) is the only critical point
7 Can 2 solution to the system intersect in the phase portrait?
7.1 Front
Can 2 solution to the system intersect in the phase portrait?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\)
7.2 Back
No, two trajectories of the solution for the system cannot intersect.
It’s similar to integral curves for direction fields, where the integral curves did not cross
8 How can we draw the easiest trajectories of this system in a phase portrait?
8.1 Front
How can we draw the easiest trajectories of this system in a phase portrait?
- \({\displaystyle \dot{x} = y}\)
- \({\displaystyle \dot{y} = x}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix}1 \\ 1\end{pmatrix} e^t + c_2 \begin{pmatrix}1 \\ -1\end{pmatrix} e^{-t}}\)
8.2 Back
Setting up \(c_{1} = c_2 = \pm 1\), we get 4 solutions
- \({\displaystyle \begin{pmatrix}1 \\ 1\end{pmatrix}e^t}\)
- \({\displaystyle - \begin{pmatrix}1 \\ 1\end{pmatrix} e^t}\)
- \({\displaystyle \begin{pmatrix}1 \\ -1\end{pmatrix}e^{-t}}\)
- \({\displaystyle - \begin{pmatrix}1 \\ -1\end{pmatrix}e^{-t}}\)
The first solution, when \(t = 0\), the point is at \((1,1)\). As \(t\) increases, the point moves outward along the line \(y = x\). As \(t\) decreases through negative values, the point moves inwards along the line, toward \((0,0)\)
Since \(t\) is always understood to be increasing on the trajectory, the whole trajectory consists of the ray \(y=x\) in the first quadrant, excluding the origin (which is not reached in finite negative time), with an outward direction of motion
Similar analysis can be made for the other 3 solutions,
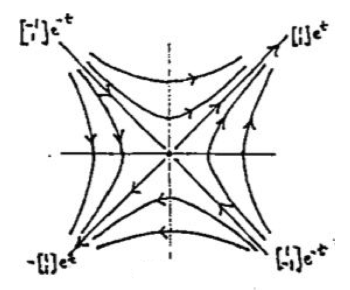
Each of the four solutions has as its trajectory one of the four rays. The indicated direction of motion is outward or inward according to whether the exponential factor increases or decreases as \(t\) increases
The origin is a fifth trajectory itself, which is a stationary point
So the intersecting diagonal lines represent five trajectories, no two of which intersect
9 Are the trajectories intersecting at point 0 for this system?
9.1 Front
Are the trajectories intersecting at point 0 for this system?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\)
9.2 Back
No, at point \((0,0)\), in this point its a solution itself

10 What can we say about this system from its phase portrait?
10.1 Front
What can we say about this system from its phase portrait?

10.2 Back
It’s a unstable saddle. It is called unstable because the trajectories go off to infinity as \(t\) increases, except at 0 and line \(y = -x\)
It’s called a saddle because of its general resemblance to the level curves of a saddle-shaped surface in 3-space
11 What can we say about this system from its phase portrait?
11.1 Front
What can we say about this system from its phase portrait?
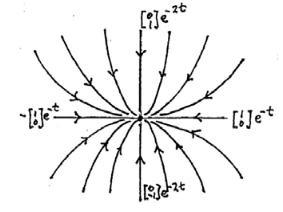
11.2 Back
It’s called an asymptotically stable node or sink node
Means that all the trajectories approach the critical point as \(t\) increases
12 What can we say about this system from its phase portrait?
12.1 Front
What can we say about this system from its phase portrait?

12.2 Back
It’s called unstable node or source node
13 What can we say about this system from its phase portrait?
13.1 Front
What can we say about this system from its phase portrait?
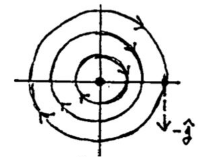
13.2 Back
It’s a stable center linear system. The word stable means that any trajectory stays within a bounded region of the phase plane as \(t\) increases or decreases indefinitely
Note: We cannot use “asymptotically stable”, since the trajectories do not approach the critical point \((0,0)\) as \(t\) increases
In this case the trajectories are circles, but you can use the word center if the curves were ellipsses having the origin as cneter
14 What can we say about this system from its phase portrait?
14.1 Front
What can we say about this system from its phase portrait?
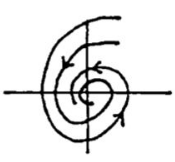
14.2 Back
Their trajectories are therefore traced out by the tip of an origin vector that rotates clockwise at a constant rate, while its magnitude shrinks exponentially to \(0\)
In other words, the trajectories spiral in toward the origin as \(t\) increases
We call this pattern as asymptotically stable spiral
15 What can we say about this system from its phase portrait?
15.1 Front
What can we say about this system from its phase portrait?
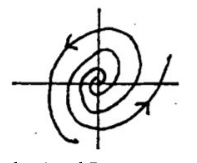
15.2 Back
The magnitude of the rotating vector increases as \(t\) increases, giving as pattern an unstable spiral
16 Draw a sketch of this linear system
16.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = y}\)
- \({\displaystyle \dot{y} = x}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix}1 \\ 1\end{pmatrix} e^t + c_2 \begin{pmatrix}1 \\ -1\end{pmatrix} e^{-t}}\)
16.2 Back
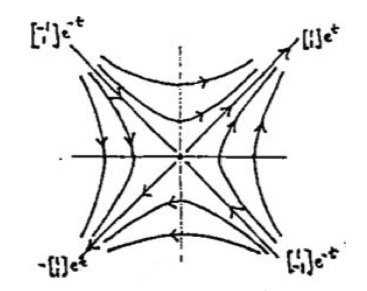
For these trajectories we can do a little algebra
- \(x = c_1 e^t + c_2 e^{-t}\)
- \(y = c_1 e^t - c_2 e^{-t}\)
This easily gives \(x^2 - y^2 = 4c_1 c_2 = k\), where \(k\) is a constant, which is the equation of a hyperbola oriented with the axes - we sketch in some of the hyperbolas.
We know which direction to point the arrows indicating the direction of motion as \(t\) increases since they must be compatible with the motion along the rays - for by continuity, nearby trajectories must have arrowheads pointing in similar directions
It’s unstable saddle
17 Draw a sketch of this linear system
17.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = -x}\)
- \({\displaystyle \dot{y} = -2y}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix}1 \\ 0\end{pmatrix} e^{-t} + c_2 \begin{pmatrix}0 \\ 1\end{pmatrix} e^{-2t}}\)
17.2 Back
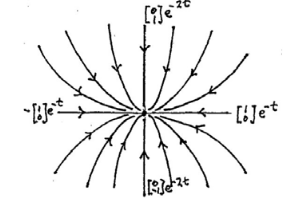
- \(x = c_1 e^{-t}\)
- \(y = c_2 e^{-2t}\)
Trajectories are a family of parabolas \(y = cx^2\)
We can see that the term \(e^{-t}\) is dominant when \(t \to \infty\), so as \(t\) increasing the solution will be parallel to the ray \({\displaystyle \begin{pmatrix}1 \\ 0\end{pmatrix}}\)
When \(t \to -\infty\), the dominant term is \(e^{-2t}\), so as \(t\) decreases the trajectories will be parallel to ray \({\displaystyle \begin{pmatrix}0 \\ 1\end{pmatrix}}\)
It’s a asymptotically stable node or sink node
18 Draw a sketch of this linear system
18.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = x}\)
- \({\displaystyle \dot{y} = 2y}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix}1 \\ 0\end{pmatrix} e^{t} + c_2 \begin{pmatrix}0 \\ 1\end{pmatrix} e^{2t}}\)
18.2 Back
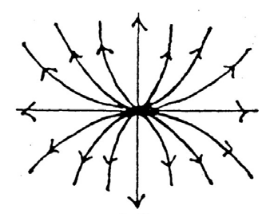
It’s an unstable node or source node
19 Draw a sketch of this linear system
19.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = y}\)
- \({\displaystyle \dot{y} = -x}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix} \sin(t) \\ \cos(t)\end{pmatrix} + c_2 \begin{pmatrix} \cos(t) \\ - \sin(t)\end{pmatrix}}\)
19.2 Back
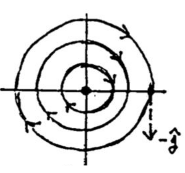
Dividing \(y’/x’\) converts to a separable first order ODE
\({\displaystyle \frac{\dv{y}{t}}{\dv{x}{t}} = \frac{\dd{y}}{\dd{x}} = - \frac{x}{y}}\)
\(x^2 + y^2 = c\)
The trajectories are the family of circles centered at the origin. The direction of motion is determined by its velocity field. You can get a velocity vector at \((1,0\) is \(\ev{0, -1} = -\vu{j}\)
So the motion is clockwise.
It’s a stable center linear system
20 Draw a sketch of this linear system
20.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = -x + y}\)
- \({\displaystyle \dot{y} = -x - y}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix}\sin(t) \\ \cos(t)\end{pmatrix} e^{-t} + c_2 \begin{pmatrix}\cos(t) \\ - \sin(t)\end{pmatrix} e^{-t}}\)
20.2 Back
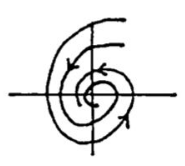
Their trajectories are therefore traced out by the tip of an origin vector that rotates clockwise at a constant rate, while its magnitude shrinks exponentially to \(0\)
In other words, the trajectories spiral in toward the origin as \(t\) increases
We call this pattern as asymptotically stable spiral
21 Draw a sketch of this linear system
21.1 Front
Draw a sketch of this linear system
- \({\displaystyle \dot{x} = x + y}\)
- \({\displaystyle \dot{y} = -x + y}\)
Which solution is \({\displaystyle \vb{u}(t) = c_1 \begin{pmatrix} \sin(t) \\ \cos(t)\end{pmatrix} e^{t} + c_2 \begin{pmatrix}\cos(t) \\ - \sin(t)\end{pmatrix} e^{t}}\)
21.2 Back
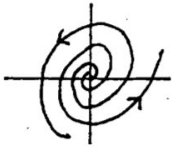
The magnitude of the rotating vector increases as \(t\) increases, giving as pattern an unstable spiral
22 Describe a general sketch for this linear system
22.1 Front
Describe a general sketch for this linear system
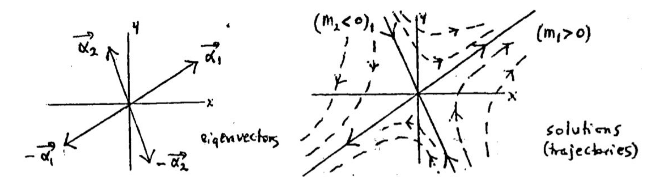
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues have opposite signs: \(\lambda_1 \gt 0\) and \(\lambda_2 \lt 0\)
22.2 Back
This is unstable saddle
Draw 4 simple solution as rays, setting \(c_1 = \pm 1\) and \(c_2 = \pm 1\) and the other to \(0\)
- \({\displaystyle \vb{x} = \pm \vb{\alpha_1} e^{\lambda_1 t}}\)
- \(\lambda_1 \gt 0\), then as \(t\) goes from \(-\infty\) to \(\infty\), this scalar factor increases from \(0\) to \(\infty\)
- A ray going out from the origin in the direction of the vector \(\vb{\alpha_1}\)
- Similar way for \(\vb{x} = - \vb{\alpha_1} e^{\lambda_1 t}\)
- \({\displaystyle \vb{x} = \pm \vb{\alpha_2} e^{\lambda_2 t}}\)
- \(\lambda_2 \gt 0\), then as \(t\) goes from \(-\infty\) to \(\infty\), this scalar factor increases from \(\infty\) to \(0\)
- A ray going out towards the origin in the direction of the vector \(\vb{\alpha_2}\)
- Similar way for \(\vb{x} = - \vb{\alpha_2} e^{\lambda_2 t}\)
- \({\displaystyle \vb{x} = \pm \vb{\alpha_1} e^{\lambda_1 t}}\)
To complete the picture, we sketch some nearby trajectories
- Smooth curves generally following the directions of the four rays described above
- They look something like hyperbolas, and they do have the rays as asymptotes
- \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + C_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
23 Describe a general sketch for this linear system
23.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues have same signs: \(\lambda_1 \lt \lambda_2 \lt 0\)
23.2 Back
It’s a asymptotically stable / sink node
The rays coming in towards the origin as \(t\) increases, since both of the \(\lambda_i\) are negative
The parabolic curves will certainly come in to the origin as \(t\) increases
- Near the origin:
- Corresponds to large positive \(t\) (\(t \gg 1\))
- The dominant term is \({\displaystyle \vb{u} \approx c_2 \vb{\alpha_2} e^{-\lambda_2 t}}\), so solution near origin are parallel to \(\alpha_2\) eigenvector
- Far from the origin:
- Corresponds to large negative \(t\) (\(t \ll -1\))
- The dominant term is \({\displaystyle \vb{u} \approx c_1 \vb{\alpha_1} e^{\lambda_1 t}}\), so solution far from the origin are parallel to \(\alpha_1\) eigenvector
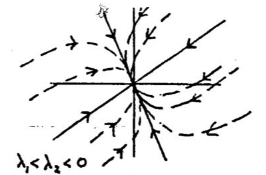
- Near the origin:
24 Describe a general sketch for this linear system
24.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues have same signs: \(\lambda_1 \gt \lambda_2 \gt 0\)
24.2 Back
It’s an unstable source node
The rays coming from the origin is outwards, since the \(\lambda_i \gt 0\)
The parabolic curves will certainly come from the origin as \(t\) increases
- Near the origin:
- Corresponds to large negative \(t\) (\(t \ll -1\))
- The dominant term is \({\displaystyle \vb{u} \approx c_2 \vb{\alpha_2} e^{\lambda_2 t}}\), so solution near origin are parallel to \(\alpha_2\) eigenvector
- Far from the origin:
- Corresponds to large positive \(t\) (\(t \gg 1\))
- The dominant term is \({\displaystyle \vb{u} \approx c_1 \vb{\alpha_1} e^{\lambda_1 t}}\), so solution far from the origin are parallel to \(\alpha_1\) eigenvector
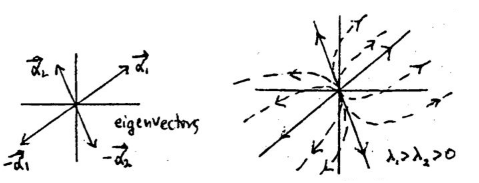
- Near the origin:
25 Describe a general sketch for this linear system
25.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues are pure imaginary: \(\lambda = \pm bi\), \(b \gt 0\)
25.2 Back
It’s a stable center linear system
Its solution has the form \({\displaystyle \vb{u} = \vb{c_1} \cos(bt) + \vb{c_2} \sin(bt)}\), where \(\vb{c_1}, \vb{c_2}\) constant vectors
Every solution is periodic, with period \({\displaystyle \frac{2\pi}{b}}\), the moving point representing it retraces its path at this interval. The trajectories are ellipses
It’s enough if you determine whether the motion is clockwise or counterclockwise. So you can get a single velocity vector \(\dot{\vb{u}}\) of the velocity field
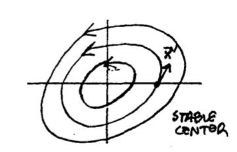
26 Describe a general sketch for this linear system
26.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues are complex: \(\lambda = a \pm bi\), \(a \lt 0\) and \(b \gt 0\)
26.2 Back
It’s asymptotically stable (sink) spiral
The solutions has the form \({\displaystyle \vb{u} = e^{at} (\vb{c_1} \cos(bt) + c_2 \sin(bt))}\), where \(\vb{c_1}, \vb{c_2}\) constant vectors
Decreases towards \(0\) as \(t \to \infty\)
Thus the point \(\vb{u}\) travels in a trajectory which is like an ellipse, except that the distance from the origin is steadily shrinking towards the origin.
Te direction of motion is calculated from a single velocity vector \(\dot{\vb{u}}\)

27 Describe a general sketch for this linear system
27.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues are complex: \(\lambda = a \pm bi\), \(a \gt 0\) and \(b \gt 0\)
27.2 Back
It’s unstable (source) spiral
The solutions has the form \({\displaystyle \vb{u} = e^{at} (\vb{c_1} \cos(bt) + c_2 \sin(bt))}\), where \(\vb{c_1}, \vb{c_2}\) constant vectors
Increases towards \(\infty\) as \(t \to \infty\)
Thus the point \(\vb{u}\) travels in a trajectory which is like an ellipse, except that the distance from the origin is steadily expanding away from the origin.
Te direction of motion is calculated from a single velocity vector \(\dot{\vb{u}}\)
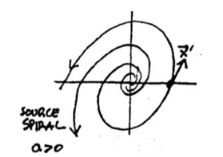
28 Describe a general sketch for this linear system
28.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues are repeated: \(\lambda \neq 0\), defective
28.2 Back
It’s incomplete, one independent eigenvector
It’s called defective node
If \(\lambda \gt 0\) is unstable, if \(\lambda \lt 0\) is asymptotically stable

29 Describe a general sketch for this linear system
29.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues are repeated: \(\lambda \neq 0\), complete
29.2 Back
You have 2 independent eigenvector corresponding to this unique \(\lambda\)
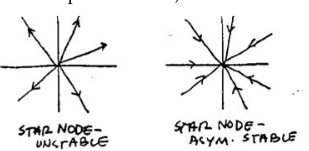
It’s called star node
If \(\lambda \gt 0\) is unstable, and if \(\lambda \lt 0\) is asymptotically stable
30 Describe a general sketch for this linear system
30.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues \(\lambda_1 = 0 \gt \lambda_2\)
30.2 Back
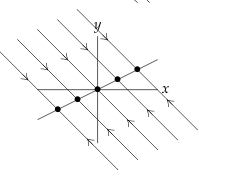
The critical points are not isolated - they lie on the line through \(0\) with direction \(\alpha_1\)
\({\displaystyle \vb{u} = c_1 \alpha_1 +c_2 \alpha_2 e^{\lambda_2 t}}\)
As \(t \to \infty\), \(\vb{u} \to c_1 \alpha_1\) along a line parallel to \(\alpha_2\)
31 Describe a general sketch for this linear system
31.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that its eigenvalues \(\lambda_1 = 0 \lt \lambda_2\)
31.2 Back
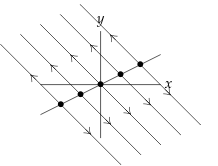
The critical points are not isolated - they lie on the line through \(0\) with direction \(\alpha_1\)
\({\displaystyle \vb{u} = c_1 \alpha_1 +c_2 \alpha_2 e^{\lambda_2 t}}\)
As \(t \to \infty\), \(\vb{u} \to \infty\) along a line parallel to \(\alpha_2\)
32 Describe a general sketch for this linear system
32.1 Front
Describe a general sketch for this linear system
\({\displaystyle \dot{\vb{x}} = A \vb{x}}\), where \(A = 2 \cross 2\) constant matrix
Which solution is \({\displaystyle \vb{u} = c_1 \vb{\alpha_1} e^{\lambda_1 t} + c_2 \vb{\alpha_2} e^{\lambda_2 t}}\)
Suppose that \(\lambda_1 = \lambda_2 = 0\)
32.2 Back
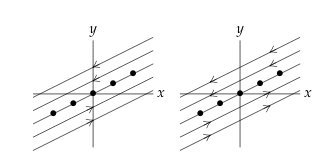
It’s a line of critical points
\({\displaystyle \vb{u} = c_1 \alpha_1 + c_2 (t \alpha_1 + \alpha_2)}\)
Trajectories are parallel to \(\alpha_1\)
33 What is the Trace Determinant graph (T-D graph)?
33.1 Front
What is the Trace Determinant graph (T-D graph)?
33.2 Back
It’s a graph where you can show the behaviour of the linear system through it’s characteristic equation \(p_A(\lambda)\)
Its abbreviations stands for \(T = \operatorname{tr}(A)\) and \(D = \operatorname{det}(A)\)
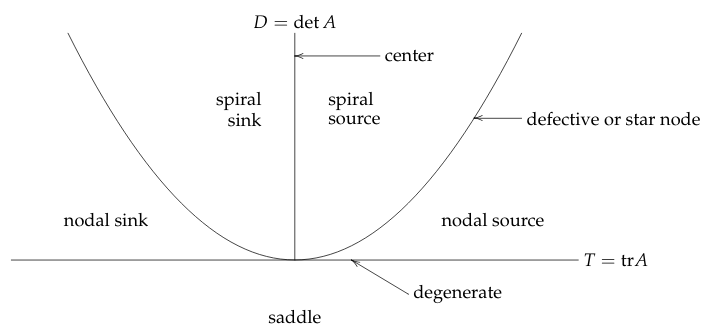
34 What is the curve which separate the real and complex eigenvalues in T-D graph?
34.1 Front
What is the curve which separate the real and complex eigenvalues in T-D graph?
34.2 Back
It’s the curve \({\displaystyle D = \frac{T^2}{4}}\)
If the discriminant of quadratic formula of the characteristic polynomial \(p_A(\lambda) = \lambda^2 - T\lambda + D\)
So, it’s root come from \({\displaystyle \lambda = \frac{T \pm \sqrt{T^2 - 4D}}{2}}\)
- \(\lambda\) is real if \(T^2 - 4D \gt 0\)
- \(\lambda\) is complex if \(T^2 - 4D \lt 0\)
35 What does mean this condition in the T-D graph?
35.1 Front
What does mean this condition in the T-D graph?
\(D \lt 0\)
Explain how is the response
35.2 Back
\({\displaystyle \lambda = \frac{T \pm \sqrt{T^2 - 4D}}{2}}\)
The eigenvalues are real and of opposite sign, hence the phase portrait is a unstable saddle
36 What does mean this condition in the T-D graph?
36.1 Front
What does mean this condition in the T-D graph?
\(0 \lt D \lt T^2/4\)
Explain how is the response
36.2 Back
\({\displaystyle \lambda = \frac{T \pm \sqrt{T^2 - 4D}}{2}}\)
The eigenvalues are real, distinct, and of the same sign, hence the phase portrait is a node
If \(T \lt 0\) is stable
If \(T \gt 0\) is unstable
37 What does mean this condition in the T-D graph?
37.1 Front
What does mean this condition in the T-D graph?
\(0 \lt T^2/4 \lt D\)
Explain how is the response
37.2 Back
\({\displaystyle \lambda = \frac{T \pm \sqrt{T^2 - 4D}}{2}}\)
The eigenvalues are neither real nor purely imaginary (are complex), hence the phase portrait is a spiral
If \(T \lt 0\) is stable
If \(T \gt 0\) is unstable
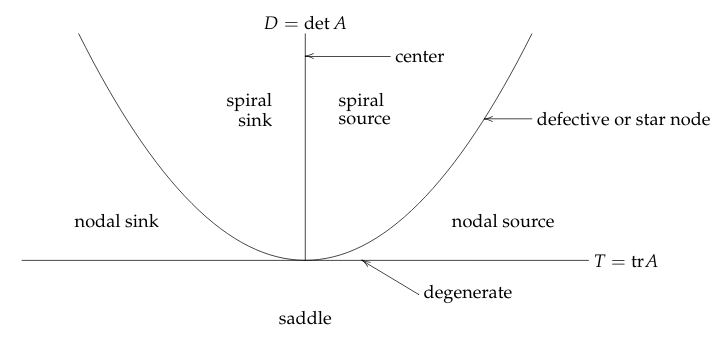
38 Describe all possible responses from the T-D graph?
38.1 Front
Describe all possible responses from the T-D graph?
38.2 Back
39 How can we determine the direction of the trajectory from this matrix
39.1 Front
How can we determine the direction of the trajectory from this matrix
\({\displaystyle \begin{pmatrix}-1 & 1 \\ 1 & -1\end{pmatrix}}\)
39.2 Back
The linear system is \({\displaystyle \dot{\vb{u}} = A \vb{u}}\), and the direction field is given by \(\dot{\vb{u}}\)
\({\displaystyle \dot{\vb{u}} = \begin{pmatrix}-1 & 1 \\ 1 & -1\end{pmatrix}}\)
- \(\dot{x} = - x + y\)
- \(\dot{y} = x - y\)
At point \((1,0)\), the velocity vector is \(\ev{-1, 1}\), which means that the trajectory is upwards
Another check is using T-D diagram for view which kind of solution is, and
check the direction of velocity field with the entry \(A_{21}\) of the matrix. In
this case is positive, so that means that it’s upwards.
40 On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is stable?
40.1 Front
On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is stable?
40.2 Back
Stable solutions occur if and only if both eigenvalues have negative real part. This happens exactly when the trace is negative an the determinant is positive - so, at all points inside the second quadrant in the T-D plane
41 On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is unstable?
41.1 Front
On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is unstable?
41.2 Back
Unstable solutions occur when there is at least one eigenvalue with positive real part. This happens either when the determinant is negative, or when the trace is positive - so, at all points inside the first, third, and fourth quadrants on the T-D plane
42 On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is neutrally stable?
42.1 Front
On the T-D plane, where can you guarantee that any matrix with that value of trace and determinant is neutrally stable?
42.2 Back
Neutrally stable solutions occur either when the trace is zero and the determinant is positive (giving periodic solutions), or when the determinant is zero and the trace is negative (giving combs)
43 On the T-D plane, are there any values of the trace and determinant for which there are matrices exhibiting more than one type of limiting behaviour?
43.1 Front
On the T-D plane, are there any values of the trace and determinant for which there are matrices exhibiting more than one type of limiting behaviour?
43.2 Back
When the trace and determinant are both zero, the zero matrix gives neutrally stable behaviour, while the matrix that has exactly one nonzero entry, in the upper right, gives unstable behaviour.
44 What is the normal mode and general solution for this linear system?
44.1 Front
What is the normal mode and general solution for this linear system?
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), where \({\displaystyle A = \begin{pmatrix}0.5 & 1 \\ -2.25 & 0.5\end{pmatrix}}\)
44.2 Back
Characteristic polynomial: \({\displaystyle p_A(\lambda) = \lambda^2 - \lambda + 2.5}\)
Eigenvalues: \({\displaystyle \lambda = \frac{1 \pm 3i}{2}}\)
Eigenvector for \({\displaystyle \lambda_1 = \frac{1 + 3i}{2}}\) satisfies \((A - \lambda_1 I) \vb{v_1}\)
Hence, \({\displaystyle \begin{pmatrix}-3i/2 & 1 \\ -9/4 & -3i/2\end{pmatrix} \vb{v_1} = \vb{0}}\)
Eigenvector: \({\displaystyle \vb{v_1} = \begin{pmatrix}1 \\ 3i/2\end{pmatrix}}\)
The normal modes: \({\displaystyle e^{(1 + 3i)t} \begin{pmatrix}1 \\ 3i/2\end{pmatrix}}\), which has
Real part of normal mode: \({\displaystyle \vb{u_1} = e^{t/2} \begin{pmatrix}\cos(3t/2) \\ - (3/2) \sin(3t/2)\end{pmatrix}}\)
Imaginary part of normal mode: \({\displaystyle \vb{u_2} = e^{t/2} \begin{pmatrix}\sin(3t/2) \\ (3/2) \cos(3t/2)\end{pmatrix}}\)
45 Suppose this IVP, is x and y increasing at t = 0?
45.1 Front
Suppose this IVP, is x and y increasing at t = 0?
\({\displaystyle A = \begin{pmatrix}0.5 & 1 \\ -2.25 & 0.5\end{pmatrix}}\)
At point \((1,0)\) of the phase portrait
45.2 Back
\({\displaystyle \dot{\vb{u}} = A \vb{u}}\), at \(t=0\) we have \(\vb{u} = \begin{pmatrix}1 \\ 0\end{pmatrix}\)
So, \({\displaystyle \dot{\vb{u}} = \begin{pmatrix}0.5 & 1 \\ -2.25 & 0.5\end{pmatrix} \begin{pmatrix}1 \\ 0\end{pmatrix} = \begin{pmatrix}0.5 \\ -2.25\end{pmatrix}}\)
So the values of \(x\) increases at \(t = 0\) with a ratio of \(0.5\), but the values of \(y\) decreases at \(t=0\) with a ratio of \(-2.25\)