- Captured On
- Source
- Linear Systems | Unit IV First-order Systems | Differential Equations | Mathematics | MIT OpenCourseWare
1 Can we solve a linear system of ODE’s with constant coefficients by eliminating variables?
1.1 Front
Can we solve a linear system of ODE’s with constant coefficients by eliminating variables?
1.2 Back
No, it’s a naive way to solve it. You need to use techniques of constant coefficient ODE methods. You can isolate a variable, and substitute in the other DE, with it’s derivatives
2 How are the solution of a linear system of ODE’s of 2x2 variables?
2.1 Front
How are the solution of a linear system of ODE’s of 2x2 variables?
2.2 Back
You will get 2 equation, 1 for each variable and apply superposition for each variable solution
3 What is a first order linear system?
3.1 Front
What is a first order linear system?
Write an example of \(n \cross n\) linear system
3.2 Back
This is a shorten from \(n \cross n\) first order linear system of ODE’s with constant coefficients which is a collection of \(n\) equation
- \(\dot{x_1} = a_{11} x_1 + \dots + a_{1n}x_n\)
- \(\dots\)
- \(\dot{x_n} = a_{n1}x_1 + \dots + a_{nn}a_n\)
where the \(a_{ij}\) are constants
4 How are the constants for this linear system ODE solutions?
4.1 Front
How are the constants for this linear system ODE solutions?
- \(x(t) = c_1 e^{0.5t} + c_2e^{0.2t}\)
- \(y(t) = 2c_3 e^{0.5t} - c_4 e^{0.2t}\)
4.2 Back
- The constants \(c_3 = c_1\) and \(c_2 = c_4\)
- For certain \(c_i\) there will be negatively-valued solutions; these are clearly not biologically significant: the model only holds for \(x,y \geq 0\)
5 Is a good method solving linear system by elimination?
5.1 Front
Is a good method solving linear system by elimination?
5.2 Back
No, it’s a method that always works but it’s the preferred techniques. You don’t need to know previous method for solving it.
In both theoretical and especially numerical work it is usually preferable to go the opposite way and convert a higher order ODE into a system of first order equations and then use matrix methods.
6 Use the method of elimination to solve the following system
6.1 Front
Use the method of elimination to solve the following system
- \(\dot{x} = x + 3y\)
- \(\dot{y} = x - y\)
6.2 Back
Let us eliminate \(x\) by solving the second equation for \(x\), so \(x = y + \dot{y}\)
Replacing \(x\) everywhere by \(y + \dot{y}\) in the first equation gives \(\ddot{y} - 4y = 0\)
Its characteristic equation is \((r -2)(r+2) = 0\), so the general solution for \(y\) is \(y = c_1 e^{2t} + c_2 e^{-2t}\)
From the solution for \(y\) and first equation, that was originally used to eliminate \(x\), we get \(x = 3c_1e^{2t} - c_2e^{-2t}\)
The solution to the system is thus
- \(x = 3c_1e^{2t} - c_2e^{-2t}\)
- \(y = c_1e^{2t} + c_2e^{-2t}\)
7 How can we write this linear system with matrix and vectors?
7.1 Front
How can we write this linear system with matrix and vectors?
- \(\dot{x} = ax + by\)
- \(\dot{y} = cx + dy\)
7.2 Back
\({\displaystyle \begin{pmatrix} \dot{x}\\ \dot{y} \end{pmatrix} = \begin{pmatrix} a & b\\ c & d \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}}\)
You can represent even more compact form. Let \({\displaystyle A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}}\) and write \(\vb{u}\) for the column vector \({\displaystyle \begin{pmatrix}x \\ y\end{pmatrix}}\)
We have \({\displaystyle \vb{\dot{u}} = \begin{pmatrix}\dot{x}(t) \\ \dot{y}(t) \end{pmatrix}}\)
and the system is simply \(\dot{\vb{u}} = A \vb{u}\)
8 Write this solution function in vector form
8.1 Front
Write this solution function in vector form
- \(x(t) = c_1 e^{0.5t} + c_2e^{0.2t}\)
- \(y(t) = 2c_1e^{0.5t} - c_2 e^{0.2t}\)
8.2 Back
\({\displaystyle \vb{u}(t) = \begin{pmatrix}c_1e^{0.5t} + c_2 e^{0.2t} \\ 2c_1 e^{0.5t} - c_2e^{0.2t}\end{pmatrix} = c_1e^{0.5t} \begin{pmatrix}1 \\ 2\end{pmatrix} + c_2 e^{0.2t} \begin{pmatrix}1 \\ -1\end{pmatrix}}\)
9 What are the normal modes of this general solution?
9.1 Front
What are the normal modes of this general solution?
\({\displaystyle \vb{u}(t) = c_1e^{0.5t} \begin{pmatrix}1 \\ 2\end{pmatrix} + c_2 e^{0.2t} \begin{pmatrix}1 \\ -1\end{pmatrix}}\)
9.2 Back
There are the column vector \(\vb{u_1}(t)\) and \(\vb{u_2}(t)\), removing the superposition
\({\displaystyle \vb{u_1}(t) = e^{0.5t} \begin{pmatrix}1 \\ 2\end{pmatrix}}\)
\({\displaystyle \vb{u_2}(t) = e^{0.2t} \begin{pmatrix}1 \\ -1\end{pmatrix}}\)
10 What is the geometry meaning of \(\vb{u}\) for this linear system?
10.1 Front
What is the geometry meaning of $\vb{u}$ for this linear system?
\({\displaystyle \dot{\vb{u}}(t) = A \vb{u}(t)}\), for a \(2 \cross 2\) linear system
10.2 Back
It plots a parametric curve on the \(xy\text{-plane}\), depends on it’s initials conditions it traces a curve in the \(xy\text{-plane}\)
11 What is the geometry meaning of \(\dot{\vb{u}}\) for this linear system?
11.1 Front
What is the geometry meaning of $\dot{\vb{u}}$ for this linear system?
\({\displaystyle \dot{\vb{u}}(t) = A \vb{u}}\)
11.2 Back
It’s plot a vector fields which measures how quickly the parametric curve \({\displaystyle \vb{u}(t)}\) traces its trajectory. It’s a velocity field
12 Which is the method to convert a second order homo. linear equation to first linear system?
12.1 Front
Which is the method to convert a second order homo. linear equation to first linear system?
Basic method name
12.2 Back
It’s called anti-elimination and Companion Matrix
13 What is the companion matrix of a DE?
13.1 Front
What is the companion matrix of a DE?
13.2 Back
It’s the corresponding coefficient matrix to the DE
14 Convert this DE to a first order linear system
14.1 Front
Convert this DE to a first order linear system
\(\ddot{x} + b \dot{x} + kx = 0\) (second order homogeneous linear equation)
Using anti-elimination
14.2 Back
Introduce a second variable defined by \(y = \dot{x}\), and substituting \(y = \dot{x}\) and \(\dot{y} = \ddot{x}\), so we get
\({\displaystyle \dot{y} + by + kx =0 \implies \dot{y} = -kx -by}\)
We now have a first order system
\begin{alignat}{2} \dot{x} & = &y&\\ \dot{y} & = -kx -b &y& \end{alignat}
The companion matrix of the equation is \({\displaystyle \begin{pmatrix}0 & 1 \\ -k & -b\end{pmatrix}}\)
15 Which is the form of a companion matrix for a second order constant coefficient DE?
15.1 Front
Which is the form of a companion matrix for a second order constant coefficient DE?
\({\displaystyle \ddot{x} + b \dot{x} + kx = 0}\)
15.2 Back
\({\displaystyle A = \begin{pmatrix}0 & 1 \\ -k & -b\end{pmatrix}}\)
16 Describe the model of population from this linear system
16.1 Front
Describe the model of population from this linear system
- \(\dot{x} = 2x - 3y\)
- \(\dot{y} = x - y\)
Explain which one it’s the prey and the predator
16.2 Back
As we can see, if \(y\) increases the ratio of \(x\), \(\dot{x}\) will decreases with a factor of 3. And if \(x\) increases then the ratio the \(y\) (\(\dot{y}\)) increases. So, we can suppose that \(y\) is the predator and \(x\) the prey. If there are more animal for \(x\) then \(y\) could eat better, but also if there are many animals of \(y\) could eat all of \(x\)
The other 2 factor could be a birth rate for \(x\) and death rate for \(y\)
17 Identify which of the trajectories correspond to each of the basic solutions
17.1 Front
Identify which of the trajectories correspond to each of the basic solutions
From this general solution
\({\displaystyle x(t) = c_1 e^{-3t} + c_2 e^{-t}}\)
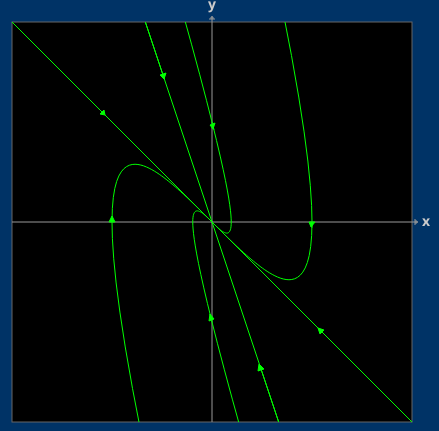
17.2 Back
Getting its derivative \({\displaystyle \dot{x}(t) = -3 c_1 e^{-3t} - c_2 e^{-t}}\), and its basic solutions are \(x_1 = e^{-3t}\), \(\dot{x_1}(t) = -3 e^{-3t}\) and \(x_2 = e^{-t}\), \(\dot{x_2}(t) = -e^{-t}\)
The ray containing \({\displaystyle \begin{bmatrix}1 \\ -1\end{bmatrix}}\) corresponds to \(x_2\) and; the ray containing \({\displaystyle \begin{vmatrix}1 \\ -3\end{vmatrix}}\) corresponds to \(x_{1}\)
18 Write down the general solution having the same trajectory
18.1 Front
Write down the general solution having the same trajectory
Initial trajectory that crosses \(x\text{-axis}\) at \(x=1\) at \(t=0\)
\({\displaystyle \vb{u}(t) = \begin{bmatrix}x(t) \\ \dot{x}(t) \end{bmatrix} = \frac{1}{2} \begin{bmatrix}3e^{-t} - e^{-3t} \\ -3e^{-t} + 3e^{-3t}\end{bmatrix}}\)
Suppose the solution has \(x(a) = 1\)
18.2 Back
\({\displaystyle \vb{u}(t) = \frac{1}{2} \begin{bmatrix}3e^{-(t - a)} - e^{-3(t - a)} \\ -3e^{-(t - a)} + 3e^{-3(t - a)}\end{bmatrix}}\)
19 Explain for a companion matrix whenever trajectory that crosses the \(x\text{-axis}\) it seems to do it perpendicularly
19.1 Front
Explain for a companion matrix whenever trajectory that crosses the $x\text{-axis}$ it seems to do it perpendicularly
Its tangent vector is vertical
19.2 Back
The velocity vector of \({\displaystyle \vb{u}(t) = \begin{bmatrix}x(t) \\ \dot{x}(t)\end{bmatrix}}\) is \({\displaystyle \dot{\vb{u}}(t) = \begin{bmatrix}\dot{x}(t) \\ \ddot{x}(t)\end{bmatrix}}\)
When \(\dot{x}(t) = 0\), then \({\displaystyle \dot{\vb{u}}(t) = \begin{bmatrix}0 \\ \ddot{x}(t)\end{bmatrix}}\), which is vertical.
Alternatively, \({\displaystyle \dot{\vb{u}} = A \vb{u}}\) and \({\displaystyle A = \begin{bmatrix}0 & 1 \\ c & d\end{bmatrix}}\), so if \({\displaystyle \vb{u} = \begin{bmatrix}x \\ 0\end{bmatrix}}\) then \({\displaystyle \dot{\vb{u}} = \begin{bmatrix}0 & 1 \\ c & d\end{bmatrix} \begin{bmatrix}x \\ 0\end{bmatrix} = x \begin{bmatrix}0 \\ c\end{bmatrix}}\), which is vertical