- Captured On
- Source
- Poles, Amplitude Response, Connection to ERF | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare
1 When can we say that a rational function is in reduced form?
1.1 Front
When can we say that a rational function is in reduced form?
1.2 Back
If the numerator \(q(s)\) and the denominator \(p(s)\) have no roots in common, then \(q(s)/p(s)\) is in reduced form
2 What is a pole for function?
2.1 Front
What is a pole for function?
2.2 Back
For a rational function in reduced form the poles are the values of \(s\) where the denominator is equal to zero
The points where the rational function is not defined
We allow the poles to be complex numbers
3 What are the poles for this function?
3.1 Front
What are the poles for this function?
\({\displaystyle \frac{1}{s^2 + 4}}\)
3.2 Back
\(s = \pm 2i\)
4 What are the poles for this function?
4.1 Front
What are the poles for this function?
\({\displaystyle s^2 + 1}\)
4.2 Back
Has no poles, it not a rational function
5 What are the poles for this function?
5.1 Front
What are the poles for this function?
\({\displaystyle \frac{1}{(s^2 + 8s + 7)(s^2 + 4)}}\)
5.2 Back
Has poles at \(-1, -7, \pm 2i\)
6 What are the poles for this function?
6.1 Front
What are the poles for this function?
\({\displaystyle \frac{s - 2}{(s^2 - 4)}}\)
6.2 Back
Put in reduced form \({\displaystyle \frac{1}{s + 2}}\), so has only one pole at \(s = -2\)
7 What the poles for a ODE’s with system function of form \(1/p(s)\)?
7.1 Front
What the poles for a ODE’s with system function of form $1/p(s)$?
7.2 Back
The poles are just the roots of \(p(s)\). These are the familiar characteristic roots.
8 Why do you draw the function \(F(s)\) with absolute values?
8.1 Front
Why do you draw the function $F(s)$ with absolute values?
8.2 Back
Because it’s a simplification of the original graph, and we can see the poles of the transfer function of the form \(1/p(s)\) easily.
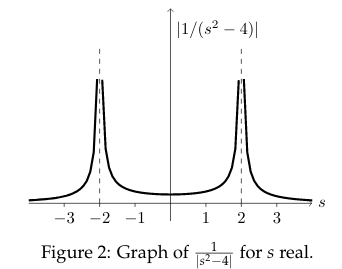
9 What are the graph to see the poles for this function?
9.1 Front
What are the graph to see the poles for this function?
\({\displaystyle F(s) = \frac{1}{s^2 - 4}}\)
Only for \(s\) real
9.2 Back
There are 2 poles at \(s = \pm 2\)
10 What is the exponential growth rate of a function \(f(t)\)?
10.1 Front
What is the exponential growth rate of a function $f(t)$?
10.2 Back
The exponential growth rate of a function \(f(t)\) is the smallest value \(a\) such that
\({\displaystyle \lim_{t \to \infty} \frac{f(t)}{e^{bt}} = 0 \qq{for all} b \gt a}\)
This says \(f(t)\) grows slower than any exponential with growth rate larger than \(a\)
11 What that means that the exponential growth rate of \(f(t)\) is positive?
11.1 Front
What that means that the exponential growth rate of $f(t)$ is positive?
11.2 Back
It means that the function \(f(t)\) grows rapidly to infinity as \(t \to \infty\)
12 What does mean that the exponential growth rate of \(f(t)\) is negative?
12.1 Front
What does mean that the exponential growth rate of $f(t)$ is negative?
12.2 Back
A negative growth rate means that the function \(f(t)\) is decaying exponentially to zero as \(t \to \infty\)
13 What is it the exponential growth rate of this function?
13.1 Front
What is it the exponential growth rate of this function?
\(e^{2t}\)
13.2 Back
\(2\)
14 What is it the exponential growth rate of this function?
14.1 Front
What is it the exponential growth rate of this function?
\(e^{-2t}\)
14.2 Back
\(-2\)
15 What is it the exponential growth rate of this function?
15.1 Front
What is it the exponential growth rate of this function?
\(f(t) = 1\)
15.2 Back
\(0\)
16 What is it the exponential growth rate of this function?
16.1 Front
What is it the exponential growth rate of this function?
\(f(t) = \cos(t)\)
16.2 Back
\(0\)
\({\displaystyle \lim_{t \to \infty} \frac{\cos(t)}{e^{bt}} = 0}\) for all positive \(b\)
17 What is it the exponential growth rate of this function?
17.1 Front
What is it the exponential growth rate of this function?
\(f(t) = t\)
17.2 Back
Has exponential growth rate \(0\)
This may be surprising because \(f(t)\) grows to infinity. But it grows linearly, which is slower than any positive exponential growth rate
18 What is it the exponential growth rate of this function?
18.1 Front
What is it the exponential growth rate of this function?
\(e^{t^2}\)
18.2 Back
Does not have an exponential growth rate since it grows faster than any exponential.
19 What is the relation between exponential growth rate and poles of \(f(t)\)?
19.1 Front
What is the relation between exponential growth rate and poles of $f(t)$?
19.2 Back
That’s a theorem
The exponential growth rate of the function \(f(t)\) is the largest real part of all poles of its Laplace transform \(\mathcal{L}(f(t))(s) = F(s)\)
20 What is it the exponential growth rate of this function?
20.1 Front
What is it the exponential growth rate of this function?
\({\displaystyle f(t) = 3e^{2t} + 5 e^t +7 e^{-8t}}\)
20.2 Back
Using the Laplace transform \({\displaystyle F(s) = \frac{3}{s - 2} + \frac{5}{s - 1} + \frac{7}{s + 8}}\), which has poles at \(s = 2, 1, -8\).
The largest real part \(s\) is \(2\)
Thus, the exponential growth rate of \(f(t)\) is \(2\)
Also, it is clear that the \(3e^{2t}\) term determines the growth rate since it is the dominant term as \(t \to \infty\)
21 What is it the exponential growth rate of this function?
21.1 Front
What is it the exponential growth rate of this function?
\({\displaystyle f(t) = e^{-t} \cos(2t) + 3e^{-2t}}\)
21.2 Back
The Laplace transform \({\displaystyle F(s) = \frac{s}{(s + 1)^2 + 4} + \frac{3}{s + 2}}\)
This has poles \(s = -1 \pm 2i, -2\)
The largest part among these is \(-1\), so the exponential growth rate is \(-1\)
22 What are the poles for this function?
22.1 Front
What are the poles for this function?
\({\displaystyle g(t) = u(t - a)f(t - a)}\), with \(a > 0\)
22.2 Back
It’s Laplace transform is \({\displaystyle G(s) = e^{-as}F(s)}\). Since \(e^{-as}\) does not have any poles, \(G(s)\) and \(F(s)\) has exactly the same poles. That is, the poles can’t detect this type of shift in time
23 What is a pole diagram?
23.1 Front
What is a pole diagram?
For function \(f(t)\)
23.2 Back
The pole diagram of a function \(F(s)\) is simply the complex s-plane with an \(X\) marking the location of each pole of \(F(s)\)
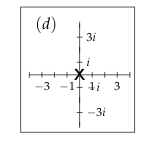
24 What is the pole diagram for this function?
24.1 Front
What is the pole diagram for this function?
\({\displaystyle F = \frac{1}{s^2 + 4}}\)
24.2 Back
25 Determine the exponential growth rate of the inverse Laplace transform
25.1 Front
Determine the exponential growth rate of the inverse Laplace transform
From the diagram
25.2 Back
The largest real part of a pole is \(-2\). The exponential growth rate is \(-2\)
26 What happens when \(t \to \infty\) for \(f(t)\) with exponential growth rate equals to \(0\)?
26.1 Front
What happens when $t \to \infty$ for $f(t)$ with exponential growth rate equals to $0$?
Poles of \(F(s)\) is \(0\)
26.2 Back
We can’t tell how \(f(t)\) behaves.
For example, if \(F(s) = \frac{1}{s}\) then \(f(t) = 1\), which stays bounded
if \(F(s) = \frac{1}{s^2}\), then \(f(t) = t\) which goes go to infinity, but more slowly than any positive exponential
27 Determine how will be \(f(t)\) as \(t \to \infty\) from its pole diagram?
27.1 Front
Determine how will be $f(t)$ as $t \to \infty$ from its pole diagram?
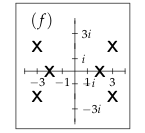
27.2 Back
Exponential growth rate is \(3\), so \(f(t) \to \infty\)
28 What is the pole diagram for a LTI system?
28.1 Front
What is the pole diagram for a LTI system?
28.2 Back
Is the pole diagram of its transfer function
29 What is the pole diagram for this system?
29.1 Front
What is the pole diagram for this system?
\({\displaystyle \ddot{x} + 4 \dot{x} + 6x = \dot{y}}\), consider \(y(t)\) to be the input
29.2 Back
Assuming rest IC’s, Laplace transforming this equation gives us
\({\displaystyle (s^2 + 4s + 6)X = sY}\)
This implies that \({\displaystyle X(s) = \frac{s}{s^2 + 4s + 6} Y(s)}\) where its transfer function is \({\displaystyle W(s) = \frac{s}{s^2 + 4s + 6}}\)
This has poles at \(s = -2 \pm \sqrt{2}i\)
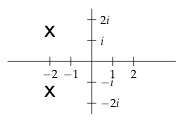
30 When can we say that a system is stable?
30.1 Front
When can we say that a system is stable?
Given its transfer function
30.2 Back
The system is stable if all its poles have negative real part
Equivalently, the system is stable if all its poles lie strictly in the left half of the complex plane \(\operatorname{Re}(s) \lt 0\)
31 Is this system stable?
31.1 Front
Is this system stable?
which pole diagram of an LTI is
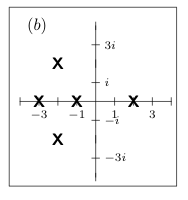
31.2 Back
No, it isn’t stable because one of its pole has positive real part
32 Which of these LTI system are stable?
32.1 Front
Which of these LTI system are stable?
Pole diagrams
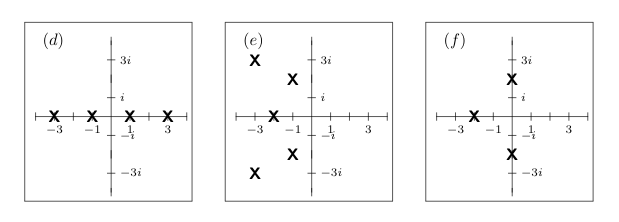
32.2 Back
Only (e) has all its poles in the left half-plane, so all it’s poles has negative real part
33 At which point could we say that the amplitude of the LTI will be largest?
33.1 Front
At which point could we say that the amplitude of the LTI will be largest?
From its pole diagram
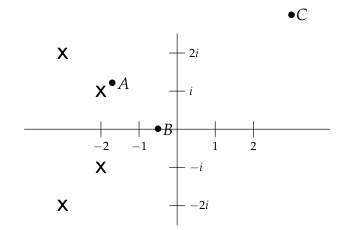
33.2 Back
We are looking form \(\abs{F(s)}\) that we know that goes to infinfite at the poles of the transfer function.
The can say that the point \(A\) will generate the largest amplitude because it close to a pole. The point \(B\) and \(C\) are both far from poles so it’ll produce a smaller amplitude than \(A\)
34 What is the relationship between amplitude response and system function?
34.1 Front
What is the relationship between amplitude response and system function?
Consider the system \(p(D) x = f(t)\)
34.2 Back
The transfer function is \({\displaystyle W(s) = \frac{1}{p(s)}}\)
When \(f(t) = B \cos(\omega t)\), the ERP is
\({\displaystyle x_p(t) = \frac{B \cos(\omega t - \phi)}{\abs{p(i\omega)}}}\), where \(\phi = \operatorname{Arg}(p(i\omega))\)
If the system is stable, then all solutions are asymptotic to the period function \(x_p(t)\)
The amplitude response is \({\displaystyle g(\omega) = \frac{1}{\abs{p(i\omega)}}}\), so comparing with its transfer function
\({\displaystyle g(\omega) = \abs{W(i\omega)}}\)
This relationship holds for all stable LTI systems
35 At approximately what frequency will the system have the biggest response?
35.1 Front
At approximately what frequency will the system have the biggest response?
This is the pole diagram of a stable LTI system
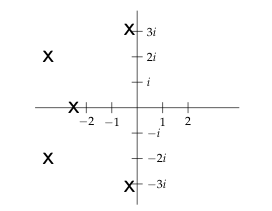
35.2 Back
Let \(W(s)\) be the transfer function, which amplitude response if \({\displaystyle g(\omega) = \abs{W(i\omega)}}\)
Since \(i\omega\) is on the positive imaginary axis, the amplitude response \(g(\omega)\) will be the largest point at the \(i\omega\) on the imaginary axis where \(\abs{W(i\omega)}\) is largest.
Thus, we choose \(i\omega \approx 3i\), i.e. the practical resonant frequency is approximately \(\omega = 3\)
You can see better in 3D
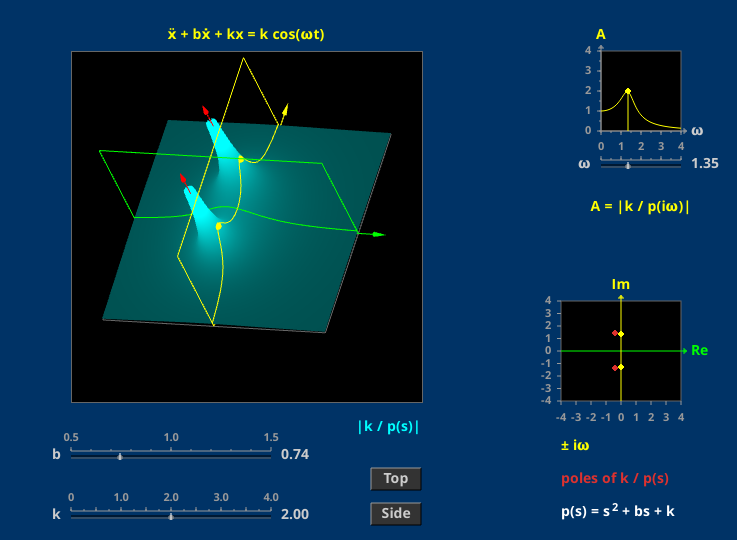
The yellow amplitude curve runs along-side the “mountains” that rise up near the poles. As \(i\omega\) gets close to a pole, the amplitude curve moves up the side of the mountain.
36 Which system decays faster?
36.1 Front
Which system decays faster?
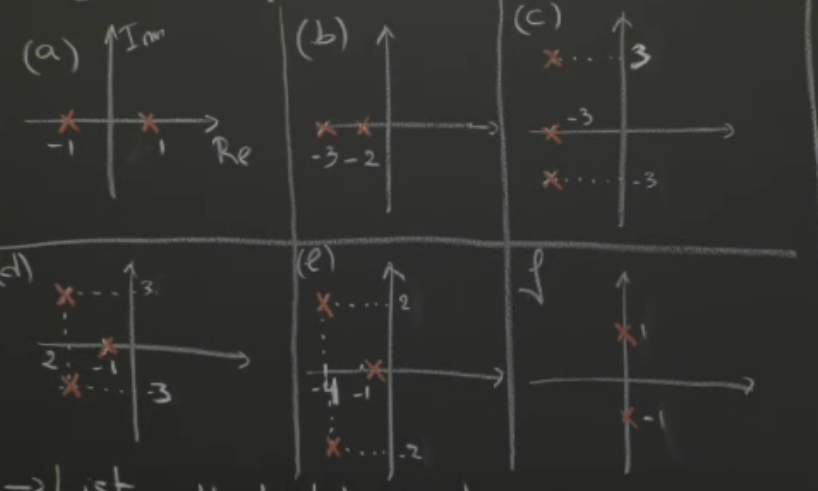
Order the system which decays in terms of velocity. And say which one has no oscillation
36.2 Back
We need to compare the rightmost pole are most on the left
- \(e^{-3t}\)
- \(e^{-2t}\)
- \(e^{-t}\)
- \(e^{-0.5t}\)
No oscillation is b
37 Consider this \(f(t)\) which values of \(\omega\) creates the biggest response?
37.1 Front
Consider this $f(t)$ which values of $\omega$ creates the biggest response?
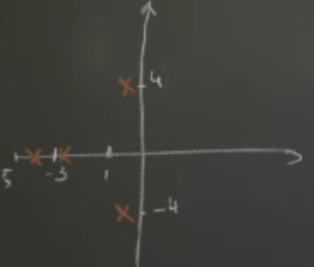
\(p(D) y = f(t)\), where \(f(t)=f_0 \cos(\omega t)\)
37.2 Back
Amplitude response is \({\displaystyle \frac{1}{\abs{p(i\omega)}}}\)
The amplitude is biggest when the polynomial \(p(s)\) is close to \(0\). So need to close the value for \(i\omega\) close to pole in the imaginary axis.
In this case \(i\omega = i4\), that is close to the pole which generate a big amplitude response.
Amplitude response is a function on terms of \(i\omega\) (along imaginary axis), over a surface described by the transfer function.
38 Find the pole diagram of \(F(s)\)
38.1 Front
Find the pole diagram of $F(s)$
\({\displaystyle f(t) = \cos(2t) + e^{-t} \sin(t)}\)
38.2 Back
\({\displaystyle \mathcal{L}(s) = \frac{s}{s^2 + 4} + \frac{1}{(s+1)^1 + 1}}\)
This has poles when \(s^2 + 4 = 0\), so at \(s = \pm 2i\), and when \((s+1)^2 + 1 = 0\), so also at \(s = -1 \pm i\)
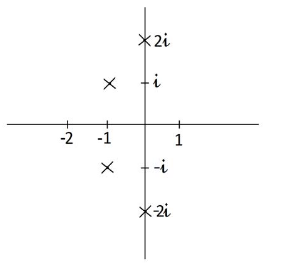
39 From this pole diagram, describe all function \(f(t)\) whose Laplace transform have given poles?
39.1 Front
From this pole diagram, describe all function $f(t)$ whose Laplace transform have given poles?
Poles: \({1, i, -i}\)
39.2 Back
For large \(t\), these functions have exponential growth rate \(e^t\). This means that for any \(a \lt 1 \lt c\), \(e^{at} \lt \abs{f(t)} \lt e^{ct}\) for large \(t\)
They also show a small oscillation of approximately constant amplitude and circular frequency \(1\)
\(f(t) = ae^t + b \sin(t)\) where \(a,b \neq 0\) with \({\displaystyle F(s) = \frac{a}{s-1} + \frac{b}{s^2 + 1}}\)
40 From this pole diagram, describe all function \(f(t)\) whose Laplace transform have given poles?
40.1 Front
From this pole diagram, describe all function $f(t)$ whose Laplace transform have given poles?
Poles: \(-1 + 4i, -1 - 4i\)
40.2 Back
For large \(t\), these functions show exponential decay like \(e^{-t}\), and oscillate with circular frequency \(4\)
\({\displaystyle f(t) = ae^{-t} \sin(4t)}\), where \(a \neq 0\) with \({\displaystyle F(s) = \frac{4a}{(s+1)^2 + 16}}\)
41 From this pole diagram, describe all function \(f(t)\) whose Laplace transform have given poles?
41.1 Front
From this pole diagram, describe all function $f(t)$ whose Laplace transform have given poles?
Poles: No have poles on the diagram
41.2 Back
For large \(t\), these functions decays to zero faster than any exponential
\(f(t) = a \delta(t-b)\) where \(a \neq 0\) and \(b \geq 0\) with \({\displaystyle F(s) = ae^{-bt}}\), or \(f(t) = a(u(t) - u(t-b))\), where \(a \neq 0, b \gt 0\) with \({\displaystyle F(s) = a \frac{1 - e^{-bs}}{s}}\)