1 Compute with the definition the Laplace transform of \(f’\)
1.1 Front
Compute with the definition the Laplace transform of $f’$
\({\displaystyle \mathcal{L}(f’)(s)}\)
Don’t do by heart
1.2 Back
\({\displaystyle \mathcal{L}(f’) = \int_{0^-}^{\infty} f’(t) e^{-st} \dd{t}}\)
Integrating by parts
- \(u = e^{-st}\), \(\dd{u} = -s e^{-st} \dd{t}\)
- \(\dd{v} = f’(t) \dd{t}\), \(v = f(t)\)
\({\displaystyle f(t) e^{-st} \bigg|_{0^-}^{\infty} + s \int_{0^-}^{\infty} f(t) e^{-st} \dd{t} = -f(0^-) + s F(s)}\)
The last equality follows from
- We assume \(f(t)\) has exponential order, so if \(\operatorname{Re}(s)\) is large enough \(f(t)e^{-st}\) is \(0\) as \(t \to \infty\)
- The integral in the second term is none other than the Laplace transform of \(f(t)\)
2 What is the Laplace transform of \(f’\)?
2.1 Front
What is the Laplace transform of $f’$?
by heart
2.2 Back
\({\displaystyle \mathcal{L}(f’) = sF(s) - f(0^-)}\)
3 What is the Laplace transform of \(f^{(n)}\)?
3.1 Front
What is the Laplace transform of $f^{(n)}$?
by heart
3.2 Back
\({\displaystyle \mathcal{L}(f^{(n)}) = s^n F(s) - s^{n-1}f(0^-) - s^{n-2}f’(0^-) + \dots - f^{(n-1)(0^-)}}\)
4 What happens with all annoying terms of the Laplace transform of \(f^{(n)}\)?
4.1 Front
What happens with all annoying terms of the Laplace transform of $f^{(n)}$?
\(f(0^-)\), \(f’(0^-)\) with rest IC
4.2 Back
All these annoying terms are 0
5 What is the Laplace transform of \(f^{(n)}\) with rest IC?
5.1 Front
What is the Laplace transform of $f^{(n)}$ with rest IC?
\({\displaystyle \mathcal{L}(f^{(n)})}\)
5.2 Back
\({\displaystyle \mathcal{L}(f^{(n)}) = s^n F(s)}\)
6 Compute the Laplace transform of this expression with two different ways
6.1 Front
Compute the Laplace transform of this expression with two different ways
\({\displaystyle f(t) = t^2 + 2t + 1}\), compute \(\mathcal{L}(f’’)\)
6.2 Back
- Directly: \({\displaystyle f’’(t) = 2t \implies \mathcal{L}(f’’) = \frac{2}{s}}\)
- Using rule: \({\displaystyle \mathcal{L}(f’’) = s^2 F(s) - sf(0^-) - f’(0^-) = s^2(\frac{2}{s^3} + \frac{2}{s^2} + \frac{1}{s}) - s \cdot 1 - 2 = \frac{2}{s}}\)
7 Proof that this Laplace transform is valid
7.1 Front
Proof that this Laplace transform is valid
\({\displaystyle \mathcal{L}(tf)(s) = -F’(s)}\)
7.2 Back
\({\displaystyle F(s) = \int_{0^-}^{\infty} f(t) e^{-st} \dd{t}}\)
\({\displaystyle F’(s) = \dv{s} \int_{0^-}^{\infty} f(t) e^{-st} \dd{t} = \int_{0^-}^{\infty} -t f(t) e^{-st} \dd{t} = - \mathcal{L}(tf(t))}\)
8 What is the Laplace transform of this expression?
8.1 Front
What is the Laplace transform of this expression?
\({\displaystyle \mathcal{L}(t^n f)(s)}\)
8.2 Back
\({\displaystyle \mathcal{L}(t^n f)(s) = (-1)^n F^{(n)}(s)}\)
9 What is the t-derivative rule of Laplace Transform?
9.1 Front
What is the t-derivative rule of Laplace Transform?
9.2 Back
- \({\displaystyle \mathcal{L}(f’) = sF(s) - f(0^-)}\)
- \({\displaystyle \mathcal{L}(f’’) = s^2 F(s) -s f(0^-) - f’(0^-)}\)
- \({\displaystyle \mathcal{L}(f^{(n)}) = s^n F(s) - s^{n-1}f(0^-) - s^{n-2}f’(0^-) + \dots - f^{(n-1)}(0^-)}\)
10 What is the s-derivative rule of Laplace Transform?
10.1 Front
What is the s-derivative rule of Laplace Transform?
10.2 Back
- \({\displaystyle \mathcal{L}(tf) (s) = -F’(s)}\)
- \({\displaystyle \mathcal{L}(t^n f)(s) = (-1)^n F^{(n)}(s)}\)
11 What is the Laplace transform of this expression?
11.1 Front
What is the Laplace transform of this expression?
\({\displaystyle \mathcal{L}(t \sin(\omega t))}\)
11.2 Back
Let \(f(t) = \sin(\omega t)\). We know that \({\displaystyle F(s) = \frac{\omega}{s^2 + \omega^2}}\)
The s-derivative rule implies
\({\displaystyle \mathcal{L}(t \sin(\omega t)) = -F’(s) = \frac{2 \omega s}{(s^2 + \omega^2)^2}}\)
12 Is the Laplace transforms inverse unique?
12.1 Front
Is the Laplace transforms inverse unique?
For example \({\displaystyle \mathcal{L}^{-1}(\frac{1}{s})}\)
12.2 Back
No, it’s not unique for example \({\displaystyle \mathcal{L}(u) = \int_{0^-}^{\infty} u(t) e^{-st} \dd{t} = \frac{1}{s}}\)
So \(f(t) = 1\) and \(f(t) = u(t)\) has the same \(\mathcal{L}f = \frac{1}{s}\)
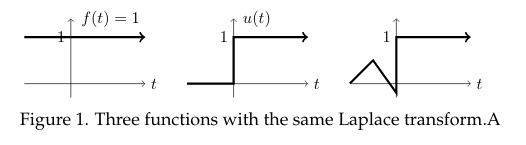
For Laplace transform we are only concerned with the interval \((0^-, \infty)\)
13 Which properties could has \(f(t)\) to be a Laplace inverse of \(F(s)\)?
13.1 Front
Which properties could has $f(t)$ to be a Laplace inverse of $F(s)$?
Enumerate \(f(t)\) properties to be called its Laplace inverse \({\displaystyle \mathcal{L}^{-1} (F)}\)
13.2 Back
- \(f(t)\) is a (possibly) generalized function
- \(f(t)\) is defined on \((0, \infty)\), except possibly at a discrete set of points where there are jump discontinuities or \(f(t)\) is singular, e.g. has delta functions.
- \(f(t)\) may also have a singular part at \(t = 0\), e.g. contains \(\delta(t)\)
- \(\mathcal{L}(f) = F\)
- In particular, the Laplace inverse is not defined at \(t = 0\) and has nothing to say about \(f(0^-)\), \(f’(0^-)\), \(f’’(0^-)\), … Indeed, it has nothing to say about \(f(t)\) for all \(t < 0\). When finding the inverse Laplace transform these values are either irrelevant or must be determined by other means.
14 What can we say about \(f(t)\) for \(t < 0\) extracted as the Laplace inverse of \(F(s)\)?
14.1 Front
What can we say about $f(t)$ for $t < 0$ extracted as the Laplace inverse of $F(s)$?
14.2 Back
It has nothing to say, the values of \(f(t)\) for \(t < 0\) are irrelevant when you get \(f(t)\) as the Laplace inverse of \(F(s)\)
15 Could \(f(t)\) as a Laplace inverse contains singular part at \(t=0\)?
15.1 Front
Could $f(t)$ as a Laplace inverse contains singular part at $t=0$?
15.2 Back
Yes, \(f(t)\) may have a singular part at \(t = 0\), e.g. contains \(\delta(t)\)
16 Must the Laplace inverse be defined at \(t = 0\)?
16.1 Front
Must the Laplace inverse be defined at $t = 0$?
16.2 Back
No, it’s not necessary. The Laplace inverse \(f(t)\) is defined for \((0, \infty)\)
17 Could be all of these function the Laplace inverse of \(F(s)\)?
17.1 Front
Could be all of these function the Laplace inverse of $F(s)$?

17.2 Back
Yes, there are all different for \(t \lt 0\) and the last two are not defined at \(t = 0\). Since they agree on \(t \gt 0\) (and have no delta function at \(t = 0\)) they have the same Laplace transform.
18 Could be any of these function be the Laplace inverse of \(F(s)\)?
18.1 Front
Could be any of these function be the Laplace inverse of $F(s)$?
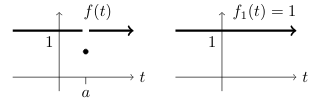
18.2 Back
Yes, they differ only at the point \(t = a\) but both has the same Laplace transform. This is because the integral is an area and the areas under two curves that differ like these are the same.
The continuous function \(f_1 (t)\) is usually a better choice
19 What is a removable discontinuity on \(f(t)\)?
19.1 Front
What is a removable discontinuity on $f(t)$?
19.2 Back
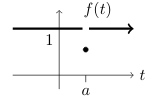
This discontinuity could be removable by changing the value of \(f(a)\) to 1
Technically, \(f(a^-) = f(a^+) = b\), so we can make a new function, continuous at \(a\) by redefining the value at \(t = a\)
\({\displaystyle f_1(t) = \begin{cases} f(t) &\text{for } t \neq a\\\ b &\text{for } t =a \end{cases} }\)
We say that discontinuity at \(t = a\) is removable
20 Solve this DE using Laplace transform
20.1 Front
Solve this DE using Laplace transform
\(\dot{x} + 3x = e^{-t}\) with rest IC
Explain the process. Set the relationships with other methods of resolution
20.2 Back
Rest IC mean that \(x(t) = 0\) for \(t \lt 0\), so \(x(0^-)\), \(\dot{x}(0^-)\),… all are \(0\)
As usual, let \(X = \mathcal{L}(x)\)
Using the t-derivative rule we can take the Laplace transform of (both sides) of the DE
\({\displaystyle (sX(s) - f(0^-)) + 3X(s) = \frac{1}{s + 1}}\)
Next we substitute the known value \(x(0^-) = 0\) and solve for \(X(s)\)
\({\displaystyle (s + 3)X(s) = \frac{1}{s + 1} \implies X(s) = \frac{1}{(s+1)(s+3)}}\)
Finally, we find \(x(t) = \mathcal{L}^{-1}(X)\) by using cover-up to do the partial fractions decomposition
\({\displaystyle \frac{1}{(s + 1)(s + 3)} = \frac{1}{2(s+1)} - \frac{1}{2(s + 3)} \implies x(t) = \frac{1}{2} e^{-t} - \frac{1}{2} e^{-3t}}\) for \(t \gt 0\)
Notes:
- The term \({\displaystyle \frac{e^{-t}}{2}}\) is what the ERF (exponential response formula) would give us
- The term \({\displaystyle \frac{e^{-3t}}{2}}\) is the homogeneous part of the solution, needed to match the IC
- Laplace transform method found \(x(t)\) for \(t < 0\). Rest IC tell us \(x(t)\) for \(t < 0\)
- \(x(0^+) = 0\) since the input does not contains \(\delta(t)\). There is no jump in \(x(t)\) at \(t = 0\)
- The factor \(s + 3\) in front of \(X(s)\) is the characteristic polynomial of this system
21 Find the unit impulse response for the system \(p(D)x = f\) using Laplace transform
21.1 Front
Find the unit impulse response for the system $p(D)x = f$ using Laplace transform
Where \(p(D) = D^2 + 2D + 2I\), consider \(f\) to be the input.
Explain the values for \(w(0^-)\), \(\dot{w}(0^-)\), \(w(0^+)\) and \(\dot{w}(0^+)\)
21.2 Back
IVP: \({\displaystyle \ddot{w} + 2 \dot{w} + 2w = \delta(t)}\) with rest IC
Laplace: \({\displaystyle s^2W + 2sW + 2W = 1 \implies W = \frac{1}{s^2 + 2s + 2}}\) (Here we left out all the ‘annoying terms’ because they are all 0 due to the rest IC)
Complete the square: \({\displaystyle s^2 + 2s + 2 = (s + 1)^2 + 1}\)
Inverse Laplace (using s-shift rule):
\({\displaystyle W = \frac{1}{(s + 1)^2 + 1} \implies w(t) = e^{-t} \mathcal{L}^{-1} (\frac{1}{s^2 + 1}) = e^{-t} \sin(t)}\) for \(t > 0\)
Thus: \({\displaystyle w(t) = u(t) e^{-t} \sin(t) = \begin{cases} 0 &\text{for } t \lt 0 \\\ e^{-t} \sin(t) &\text{for } t \gt 0 \end{cases} }\)
- \(w(0^-) = \dot{w}(0^-) = 0\)
- Post-initial conditions emerge naturally from the solution and are \(w(0^+) = 0\), \(\dot{w}(0^+) = 1\)
- Since \(\dot{w}(0^-) = 0\) the first derivative jumps by \(1\) unit at \(t = 0\)
- \((s^{2 + 2s + 1)}\) is the characteristic polynomial
22 Solve this IVP using Laplace transform
22.1 Front
Solve this IVP using Laplace transform
\(\dot{x} + 2x = 4t\) with initial condition \(x(0) = 1\)
22.2 Back
Because the input contains no delta function it is okay to specify the initial condition at \(t = 0\) instead of \(t = 0^-\). There will no jump in the output \(x(0) = x(0^-) = x(0^+)\)
Laplace: \({\displaystyle sX - x(0^-) + 2X = \frac{4}{s^2}}\)
Algebra and partial fractions
\({\displaystyle X(s) = \frac{4}{s^2(s+2)} + \frac{1}{s + 2} = \frac{A}{s} + \frac{B}{s^2} + \frac{C}{s + 2} + \frac{1}{s + 2}}\)
Cover-up gives
- \(B = 2\)
- \(C = 1\)
Undetermined coefficients gives
- \(A = -1\)
Inverse Laplace:
\(x(t) = -1 + 2t + 2e^{-2t}\) for \(t \gt 0\)
23 Solve this IVP using Laplace transform
23.1 Front
Solve this IVP using Laplace transform
\(\ddot{x} + 4x = \cos(2t)\) with rest IC
23.2 Back
Laplace: \({\displaystyle (s^2 + 4)X(s) = \frac{s}{s^2 + 4} \implies X(s) = \frac{s}{(s^2 + 4)^2}}\)
Inverse Laplace: \({\displaystyle x(t) = \frac{t \sin(2t)}{4}}\)
Notes:
- This is a response of pure resonance
24 Consider this system and its unit impulse response…
24.1 Front
Consider this system and its unit impulse response…
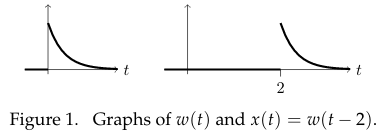
\(\dot{x} + 3x = f(t)\), \(w(t) = u(t) e^{-3t}\)
What is the response if \(f(t) = \delta(t - 2)\) with rest IC?
Graph both responses
24.2 Back
LTI (Linear Time Invariance) tell us the response will also be shifted
\({\displaystyle x(t) = w(t - 2) = u(t -2) e^{-3(t - 2)}}\)
25 What is the t-translation rule for Laplace transform?
25.1 Front
What is the t-translation rule for Laplace transform?
Tip: Delta and Heaviside functions
25.2 Back
- \({\displaystyle \mathcal{L}(u(t - a)f(t - a)) = e^{-as} F(s)}\)
- \({\displaystyle \mathcal{L}(u(t - a)f(t)) = e^{-as} \mathcal{L}(f(t + a))}\)
- \({\displaystyle \mathcal{L}(u(t - a)) = \frac{e^{-as}}{s}}\)
- \({\displaystyle \mathcal{L}(\delta(t - a)) = e^{-as}}\)
26 What is the inverse Laplace transform for \(e^{-as}F(s)\)?
26.1 Front
What is the inverse Laplace transform for $e^{-as}F(s)$?
26.2 Back
\({\displaystyle u(t - a)f(t - a)}\)
27 What is the inverse Laplace for this expression?
27.1 Front
What is the inverse Laplace for this expression?
\({\displaystyle \mathcal{L}^{-1} \biggl(\frac{k e^{-as}}{s^2 + k^2} \biggr)}\)
27.2 Back
\({\displaystyle f(t) = \mathcal{L}^{-1} \biggl( \frac{k}{s^2 + k^2} \biggr) = \sin(kt)}\)
So, \({\displaystyle \mathcal{L}^{-1} \biggl(\frac{k e^{-as}}{s^2 + k^2} \biggr) = u(t - a) f(t - a) = u(t -a) \sin(k(t -a))}\)
28 What is the Laplace transform of \((u(t - 3)t\)?
28.1 Front
What is the Laplace transform of $(u(t - 3)t$?
\({\displaystyle \mathcal{L}(u(t - 3)t)}\)
28.2 Back
\({\displaystyle e^{-3s} \mathcal{L}(t + 3) = e^{-3s} \biggl(\frac{1}{s^2} + \frac{3}{s} \biggr)}\)
29 What is the Laplace transform of this expression?
29.1 Front
What is the Laplace transform of this expression?
\({\displaystyle \mathcal{L}(u(t - 3) \cdot 1)}\)
29.2 Back
\({\displaystyle e^{-3s} \mathcal{L}1} = \frac{e^{-3s}}{s}\)
30 What is the Laplace transform of this expression?
30.1 Front
What is the Laplace transform of this expression?
\({\displaystyle f(t) = \begin{cases} 0 &\text{for } t \lt 2 \\\ t^2 &\text{for } t \gt 2 \end{cases} }\)
30.2 Back
\({\displaystyle f(t) = u(t - 2)t^2 \implies F(s) = e^{-2s} \mathcal{L}((t + 2)^2) = e^{-2s} \biggl(\frac{2}{s^3} + \frac{4}{s^2} + \frac{4}{s} \biggr)}\)
31 What is the Laplace transform for this expression?
31.1 Front
What is the Laplace transform for this expression?
\({\displaystyle f(t) = \begin{cases} \cos(t) &\text{for } 0 \lt t \lt 2\pi \\\ 0 &\text{for } t \gt 2\pi \end{cases} }\)
31.2 Back
\({\displaystyle f(t) = \cos(t)(u(t) - u(t - 2\pi)) = u(t) \cos(t) - u(t -2\pi) \cos(t)}\)
\({\displaystyle F(s) = \frac{s}{s^2 + 1} - e^{-2\pi s} \mathcal{L}(\cos(t + 2\pi)) = (1 - e^{-2 \pi s}) \frac{s}{s^2 + 1}}\)
32 How is the \(f(t)\) and its Laplace transform to model this situation?
32.1 Front
How is the $f(t)$ and its Laplace transform to model this situation?
Stock a lake with fish at a constant rate of \(r\) units per year, but after half year the funding is cut and the program ends
32.2 Back
\({\displaystyle f(t) = \begin{cases} r &\text{for } 0 \lt t \lt 1/2 \\\ 0 &\text{for } 1/2 \lt t \end{cases} }\)
Using u-format: \({\displaystyle f(t) = r(1 - u(t - 1/2))}\)
Laplace: \({\displaystyle \mathcal{L}(f)(s) = F(s) = \frac{r}{s} - \frac{r}{s}e^{-s/2}}\)
33 What is the inverse Laplace for this expression?
33.1 Front
What is the inverse Laplace for this expression?
\({\displaystyle \mathcal{L}^{-1} \biggl( \frac{r e^{-s/2}}{s(s + k)} \biggr)}\)
33.2 Back
\({\displaystyle u(t-1/2) \frac{r}{k} (1 - e^{-k(t - 1/2)})}\)
34 How is the \(f(t)\) and its Laplace transform to model this situation?
34.1 Front
How is the $f(t)$ and its Laplace transform to model this situation?
Once a year \(r/2\) units of fish are dumped all at once into the lake
34.2 Back
\({\displaystyle f(t) = \frac{r}{2} (\delta(t) + \delta(t - 1) + \delta(t - 2) + \delta(t - 3) + \dots)}\)
This is called impulse train
Laplace: \({\displaystyle F(s) = \frac{r}{2} (1 + e^{-s} + e^{-2s} + e^{-3s} + \dots)}\)
35 Find the Laplace transform of \(f(t)\) by use of the t-shift rule
35.1 Front
Find the Laplace transform of $f(t)$ by use of the t-shift rule
\({\displaystyle f(t) = (u(t) - u(t - 2\pi)) \sin(t)}\)
35.2 Back
In this case we can write \(\sin(t) = \sin(t - 2 \pi)\) (since it is periodic with period \(2\pi\)). Then using the shift rule
\({\displaystyle \mathcal{L}(u(t) - u(t - 2\pi) \sin(t - 2\pi)) = \biggl(1 - e^{-2\pi s} \biggr) \biggl(\frac{1}{s^2 + 1} \biggr)}\)
36 What is the inverse Laplace of this expression?
36.1 Front
What is the inverse Laplace of this expression?
\({\displaystyle \mathcal{L}^{-1} \biggl( \frac{a}{b (as + b)} \biggr)}\)
36.2 Back
\({\displaystyle \frac{a}{b} \frac{1}{a} \mathcal{L}^{-1} \biggl(\frac{1}{s + b/a} \biggr) = \frac{1}{b} e^{- bt/a}}\)