- Captured On
- Source
- Laplace Transform: Basics | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is the definition of Laplace Transform?
1.1 Front
What is the definition of Laplace Transform?
1.2 Back
The Laplace transform of a function \(f(t)\) of a real variable \(t\) is another function depending on a new variable \(s\), which is in general complex.
We denote the Laplace transform of \(f\) by \(\mathcal{L}f\)
\({\displaystyle (\mathcal{L}f)(s) = \int_{0^-}^{\infty} f(t) e^{-st} \dd{t}}\)
for all values of \(s\) for which the integral converge.
- \(\mathcal{L}f\) is only defined for those values of \(s\) for which the improper integral converges
- \(s\) could be complex
- Under lower limit \(0^-\) is necessary for accommodate generalized functions which contains \(\delta(t)\)
- \(\mathcal{L}f\) is only concerned with functions on \((0^-, \infty)\)
2 For which values of \(s\) is defined the Laplace Transform?
2.1 Front
For which values of $s$ is defined the Laplace Transform?
\(\mathcal{L}f\)
2.2 Back
Is only defined for those values of \(s\) for which the improper integral \({\displaystyle \int_{0^-}^{\infty} f(t) e^{-st} \dd{t}}\) converges
3 Could we use complex number in the new variable \(s\) of the Laplace Transform?
3.1 Front
Could we use complex number in the new variable $s$ of the Laplace Transform?
3.2 Back
Yes, it’s allowed
4 Why do we need the lower limit \(0^{-}\) in the integral of Laplace Transform?
4.1 Front
Why do we need the lower limit $0^{-}$ in the integral of Laplace Transform?
4.2 Back
Because it necessary to accommodate generalized functions which contains \(\delta(t)\)
5 On which interval are defined the Laplace Transform functions?
5.1 Front
On which interval are defined the Laplace Transform functions?
5.2 Back
\((0^-, \infty)\)
6 How do we understood the meaning of \(F(s)\) in this formula?
6.1 Front
How do we understood the meaning of $F(s)$ in this formula?
\(\mathcal{L}(f’) = sF(s) - f(0^-)\)
6.2 Back
\(F(s) = \mathcal{L}(f) = (\mathcal{L}f)(s)\)
7 Which is the notation for write the Laplace transform of \(t^{2}\)?
7.1 Front
Which is the notation for write the Laplace transform of $t^{2}$?
7.2 Back
\(\mathcal{L}(t^{2})(s) = \mathcal{L}(t^2)\)
8 If \(f(t) = t^{2}\), what are the notation for write its Laplace Transform?
8.1 Front
If $f(t) = t^{2}$, what are the notation for write its Laplace Transform?
8.2 Back
- \((\mathcal{L}f)(s)\)
- \(F(s)\)
- \(\mathcal{L}f(s)\)
- \(\mathcal{L}(f(t))(s)\)
- \(\mathcal{L}(t^2)(s)\)
- \(\mathcal{L}f\)
- \(F\)
- \(\mathcal{L}(t^2)\)
9 Let \(f(t)=1\), find \(F(s)\)
9.1 Front
Let $f(t)=1$, find $F(s)$
Using the definition of Laplace Transform
9.2 Back
\({\displaystyle \mathcal{L}(1) = F(s) = \int_0^{\infty} e^{-st} \dd{t} = \lim_{T \to \infty} \frac{e^{-st}}{-s} \bigg|_0^T = \lim_{T \to \infty} \frac{e^{-sT} - 1}{-s}}\)
The limit depends on whether \(s\) is positive or negative
\({\displaystyle \lim_{T \to \infty} e^{-sT} = \begin{cases} 0 &\text{for } s \gt 0 \\\ \infty &\text{for } s \lt 0 \end{cases} }\)
Therefore
\({\displaystyle \mathcal{L}(1) = F(s) = \begin{cases} \frac{1}{s} &\text{for } s \gt 0 \\\ \text{diverges } &\text{for } s \leq 0 \end{cases} }\)
10 Compute this Laplace Transform
10.1 Front
Compute this Laplace Transform
\(\mathcal{L}(e^{at})\) using the definition of Laplace Transform
10.2 Back
\({\displaystyle \mathcal{L}(e^{at}) = \int_0^{\infty} e^{at} e^{-st} \dd{t} = \lim_{T \to \infty} \frac{e^{(a - s)t}}{a - s} \bigg|_0^T = \lim_{T \to \infty} \frac{e^{(a - s)T} - 1}{a - s}}\)
The limit depends on whether \(s \gt a\) or \(s \lt a\)
\({\displaystyle \lim_{T \to \infty} e^{(a -s)T} = \begin{cases} 0 &\text{if } s \gt a \\\ \infty &\text{if } s \lt a \end{cases} }\)
Therefore
\({\displaystyle \mathcal{L}(e^{at}) = \begin{cases} \frac{1}{s - a} &\text{if } s \gt a \\\ \text{diverges } &\text{if } s \leq a \end{cases} }\)
11 Are the Laplace Transform linear?
11.1 Front
Are the Laplace Transform linear?
\(\mathcal{L}(c_1 f + c_2 g)\)
11.2 Back
\(c_1 \mathcal{L}(f) + c_2 \mathcal{L}(g)\)
12 What is the Laplace Transform for \(f(t) = 1\) by heart?
12.1 Front
What is the Laplace Transform for $f(t) = 1$ by heart?
12.2 Back
\({\displaystyle F(s) = \frac{1}{s}}\) for \(s \gt 0\)
13 What is the Laplace Transform for \(f(t) = e^{at}\) by heart?
13.1 Front
What is the Laplace Transform for $f(t) = e^{at}$ by heart?
13.2 Back
\({\displaystyle F(s) = \frac{1}{s - a}}\) for \(\operatorname{Re}(s - a) \gt 0\)
14 Show that the Laplace Transform of \(e^{at}f(t) = F(s - a)\)
14.1 Front
Show that the Laplace Transform of $e^{at}f(t) = F(s - a)$
14.2 Back
\({\displaystyle \mathcal{L}(e^{at} f(t)) = \int_0^\infty e^{at} f(t) e^{-st} \dd{t} = \int_0^{\infty} f(t) e^{-(s - a)t} \dd{t} = F(s - a)}\)
That is the definition of Laplace Transform which variable is \(s - a\), valid for \(s \gt a\)
That’s is called exponential shift
15 What is the region on convergence of the Laplace Transform?
15.1 Front
What is the region on convergence of the Laplace Transform?
15.2 Back
It’s the complex region where the Laplace Transform is defined
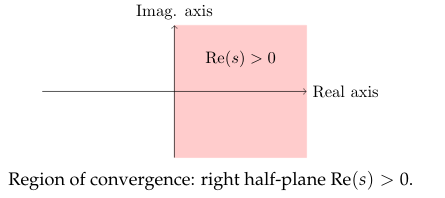
16 Compute Laplace Transform of \(f(t) = 1\) for complex \(s\)
16.1 Front
Compute Laplace Transform of $f(t) = 1$ for complex $s$
Let \(s = \alpha + i \beta\)
16.2 Back
\({\displaystyle \mathcal{L}(1)(s) = \int_0^{\infty} e^{-st} \dd{t} = \lim_{T \to \infty} \frac{e^{-st}}{-s} \bigg|_0^T = \lim_{T \to \infty} \frac{e^{-\alpha t}(\cos(\beta t) + i \sin(\beta t))}{-s} \bigg|_0^T}\)
This converges if \(\alpha \gt 0\) and diverges if \(\alpha \lt 0\). Since \(\alpha = \operatorname{Re}(s)\) we have \(\mathcal{L}(1) = 1/s\) for \(\operatorname{Re}(s) \gt 0\)
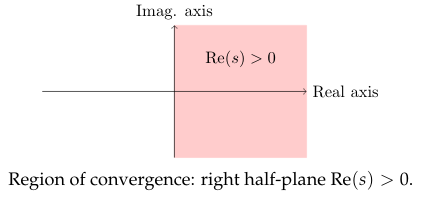
17 What does mean that the Laplace Transform is defined under the frequency view?
17.1 Front
What does mean that the Laplace Transform is defined under the frequency view?
17.2 Back
The Laplace Transform variable \(s\) can be thought of as complex frequency. The Euler’s formula says \(e^{i\omega t} = \cos(\omega t) + i \sin(\omega t)\) and we call \(\omega\) the angular frequency.
By analogy for any complex number exponent we call \(s\) the complex frequency in \(e^{st}\). If \(s = a + i \omega\) then \(s\) is the complex frequency and its imaginary part \(\omega\) is an actual frequency of a sinusoidal oscillation
18 Are there a Laplace Transform if its improper integral fails to converge?
18.1 Front
Are there a Laplace Transform if its improper integral fails to converge?
18.2 Back
No, if the integral doesn’t converge for any \(s\) then the function does not have a Laplace transform.
For example, \({\displaystyle f(t) = e^{t^2}}\)
19 When can we say that a function is of exponential order?
19.1 Front
When can we say that a function is of exponential order?
19.2 Back
A function said to be of exponential order if there are numbers \(a\) and \(M\) such that \(\abs{f(t)} \lt Me^{at}\) for all \(t\). In this case, we say that \(f\) has exponential order \(a\)
20 Which functions has exponential order \(0\)?
20.1 Front
Which functions has exponential order $0$?
20.2 Back
- \(1\)
- \(\cos(\omega t)\)
- \(\sin(\omega t)\)
21 Which functions has exponential order \(a\)?
21.1 Front
Which functions has exponential order $a$?
21.2 Back
\(e^{at}\)
22 What is a piecewise continuous function?
22.1 Front
What is a piecewise continuous function?
\(f(t)\)
22.2 Back
\(f(t)\) is a piecewise continuous function if it is continuous everywhere except at a finite number of points in any finite interval and it at these points it has a jump discontinuity (i.e. a jump of finite height)
Example: The square wave is a piecewise continuous
23 Is the square wave a piecewise continuous function?
23.1 Front
Is the square wave a piecewise continuous function?
23.2 Back
Yes, it’s
24 What can we say about the Laplace transform of this function?
24.1 Front
What can we say about the Laplace transform of this function?
\(f(t)\) is a piecewise continuous function and of exponential order \(a\)
24.2 Back
We can say that the Laplace transform \(\mathcal{L}f(s)\) converges for all \(s\) with \(\operatorname{Re}(s) \gt a\)
25 What is the value of this expression?
25.1 Front
What is the value of this expression?
\(\abs{e^{-ibt}}\)
25.2 Back
\(1\)
26 For which values of \(\alpha\) converges this improper integral?
26.1 Front
For which values of $\alpha$ converges this improper integral?
\({\displaystyle \int_0^{\infty} M e^{-\alpha t} \dd{t}}\)
26.2 Back
Converges for \(\alpha \gt 0\)
27 Could we extend the domain of \(F(s) = 1/s\)?
27.1 Front
Could we extend the domain of $F(s) = 1/s$?
For \(f(t)\) we have \(F(s) = 1/s\) with region of convergence \(\operatorname{Re}(s) \gt 0\)
27.2 Back
The function \(1/s\) is well defined for all \(s \neq 0\), so you can extend the domain of \(F(s)\) from the region of convergence by the process analytic continuation
In this class analytic continuation will always consist of extending \(F(s)\) to the complex plane minus the zeros of the denominator.
28 What is the exponential order of \(t^{n}\)?
28.1 Front
What is the exponential order of $t^{n}$?
28.2 Back
\(t^n \leq M e^t\), with \(a = 1\) is enough
\(t^{n}\) is a 1 exponential type
Proof:
\({\displaystyle \frac{t^n}{e^t} \leq M}\) for some \(M\)
\({\displaystyle \lim_{t \to \infty} \frac{t^n}{e^t} = 0}\) by L’Hop rule for \(n\) times, the denominator always will keep \(e^t\)
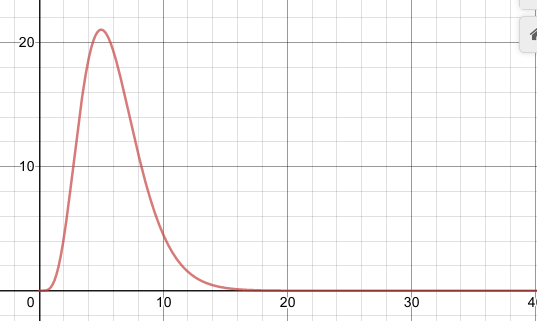
where \(M\) is the maximum point
29 Write several examples of function that are not exponential type?
29.1 Front
Write several examples of function that are not exponential type?
29.2 Back
- \({\displaystyle \frac{1}{t}}\)
- \({\displaystyle e^{t^2}}\) it grows to rapidly \(e^{t^2} \gt e^{kt}\) not matters which \(k\) you choose
30 Has \(1/t\) a Laplace transform?
30.1 Front
Has $1/t$ a Laplace transform?
30.2 Back
No because it not a exponential type function
31 Compute the Laplace transform of \(\cos\) and \(\sin\)
31.1 Front
Compute the Laplace transform of $\cos$ and $\sin$
- \(\mathcal{L}(\sin(\omega t))\)
- \(\mathcal{L}(\cos(\omega t))\)
Tip: \(\mathcal{L}(e^{a t}) = \frac{1}{s - a}\) for \(s \gt a\)
31.2 Back
Using the Laplace transform of \(e^{at}\) and Euler’s formula for the complex exponential
\({\displaystyle \mathcal{L}(\cos(\omega t) + i \sin(\omega t)) = \mathcal{L}(e^{i \omega t}) = \frac{1}{s - i\omega} = \frac{1}{s - i\omega} \cdot \frac{s + i\omega}{s + i \omega} = \frac{s + i\omega}{s^2 + \omega^2}}\)
Taking the real and imaginary parts given us the formula
- \({\displaystyle \mathcal{L}(\cos(\omega t)) = \operatorname{Re}(\mathcal{L}(e^{i \omega t})) = \frac{s}{s^2 + \omega^2}}\)
- \({\displaystyle \mathcal{L}(\sin(\omega t)) = \operatorname{Im}(\mathcal{L}(e^{i \omega t})) = \frac{\omega}{s^2 + \omega^2}}\)
The region of convergence follow from the fact that \(\cos(\omega t)\) and \(\sin(\omega t)\) both have exponential order \(0\)
32 Compute the Laplace transform of \(t^{n}\)
32.1 Front
Compute the Laplace transform of $t^{n}$
For a positive integer, \(n\)
32.2 Back
\({\displaystyle \mathcal{L}(t^n) = \int_0^{\infty} t^n e^{-st} \dd{t}}\)
Integrating by parts, where
- \({\displaystyle u = t^n}\), \({\displaystyle \dd{u} = n t^{n-1} \dd{t}}\)
- \({\displaystyle \dd{v} = e^{-st} \dd{t}}\), \({\displaystyle v = \frac{e^{-st}}{-s}}\)
\({\displaystyle \mathcal{L}(t^n) = \frac{t^n e^{-st}}{-s} \bigg|_0^{\infty} - \int_0^{\infty} \frac{n t^{n-1} e^{-st}}{-s} \dd{t}}\)
The evaluation of \({\displaystyle \frac{t^n e^{-st}}{-s} \bigg|_0^{\infty} = 0 - 0 = 0}\) for \(s > 0\)
- \({\displaystyle \frac{1}{-s} \lim_{t \to \infty} \frac{t^n}{e^{st}} = 0}\), for \(s > 0\), but diverges when \(s < 0\)
- \({\displaystyle \frac{0}{-s} = 0}\) for \(s > 0\)
Therefore
\({\displaystyle \mathcal{L}(t^n) = \frac{1}{s} \int_0^{\infty} n t^{n-1} e^{-st} = \frac{n}{s} \mathcal{L}(t^{n-1})}\)
Applying this pattern until reduction, we will get
\({\displaystyle \mathcal{L}(t^n) = \frac{n!}{s^n} \mathcal{L}(t^0) = \frac{n!}{s^n} \mathcal{L}(1) = \frac{n!}{s^n} \frac{1}{s} = \frac{n!}{s^{n+1}}}\)
33 What does mean \(F(s - z)\)?
33.1 Front
What does mean $F(s - z)$?
\(z\) could be a complex number. Describe which is its convergence too.
33.2 Back
If the s-shift formula, where \(F(s) = \mathcal{L}(f(t))\)
\(F(s - z) = \mathcal{L}(e^{zit} f(t))\), where \(z\) could be a complex number
If the region of convergence for \(\mathcal{L}f\) is \(\operatorname{Re}(s) \gt a\) then the region of convergence for \(\mathcal{L}(e^{zt} f(t))\) is \(\operatorname{Re}(s) > \operatorname{Re}(z) + a\)
34 What is the Laplace transform of \(e^{zt}\cos(\omega t)\)?
34.1 Front
What is the Laplace transform of $e^{zt}\cos(\omega t)$?
\({\displaystyle \mathcal{L}(e^{zt} \cos(\omega t))}\)
34.2 Back
\({\displaystyle \mathcal{L}(e^{zt} \cos(\omega t)) = \frac{s - z}{(s - z)^2 + \omega^2}}\)
for \(\operatorname{Re}(s) \gt \operatorname{Re}(z)\)
35 What is the Laplace transform of \(e^{zt} \sin(\omega t)\)?
35.1 Front
What is the Laplace transform of $e^{zt} \sin(\omega t)$?
\({\displaystyle \mathcal{L}(e^{zt} \sin(\omega t))}\)
35.2 Back
\({\displaystyle \mathcal{L}(e^{zt} \sin(\omega t)) = \frac{\omega}{(s - z)^2 + \omega^2}}\)
for \(\operatorname{Re}(s) \gt \operatorname{Re}(z)\)
36 What is the Laplace transform of \(\delta(t)\)?
36.1 Front
What is the Laplace transform of $\delta(t)$?
\({\displaystyle \mathcal{L}\delta(t)}\)
36.2 Back
\({\displaystyle \mathcal{L}\delta(t) = \int_{0^-}^{\infty} \delta(t) e^{-st} \dd{t} = 1}\) for all \(s\)
37 What is the Laplace transform of \(\delta(t - a)\)?
37.1 Front
What is the Laplace transform of $\delta(t - a)$?
\({\displaystyle \mathcal{L}(\delta(t - a))}\) for \(a > 0\)
37.2 Back
\({\displaystyle \mathcal{L}(\delta(t - a)) = \int_{0^-}^{\infty} \delta(t - a)e^{-st} \dd{t} = e^{-as}}\) for the region of convergence all \(s\)
If \(a = 0\), then we will get \(1\), otherwise the improper integral will not converge
38 What is the Laplace transform of \((1 + t)^{2}\)?
38.1 Front
What is the Laplace transform of $(1 + t)^{2}$?
\({\displaystyle \mathcal{L}(1 + t)^2}\)
38.2 Back
\({\displaystyle \mathcal{L}(1 + t)^2 = \frac{1}{s} + \frac{2}{s^2} + \frac{2!}{s^{3}}}\)
39 What is the Laplace transform of this expression?
39.1 Front
What is the Laplace transform of this expression?
\({\displaystyle \mathcal{L}(e^{-t}(t^2 + 1))}\)
39.2 Back
By linearity and the formulas, \({\displaystyle \mathcal{L}(t^2 + 1) = \frac{2}{s^3} + \frac{1}{s} = \frac{2 + s^2}{s^3}}\)
By s-shift, \({\displaystyle \mathcal{L}(e^{-t} (t^2 + 1)) = \frac{2 + (s + 1)^2}{(s+1)^3} = \frac{s^2 + 2s + 3}{(s + 1)^3}}\)
40 Find a formula for the Laplace transform \(g(t) = f(at)\) in terms of \(F(s)\)
40.1 Front
Find a formula for the Laplace transform $g(t) = f(at)$ in terms of $F(s)$
Suppose that \(F(s)\) is the Laplace transform of \(f(t)\) and \(a \gt 0\)
40.2 Back
\({\displaystyle G(s) = \int_0^{\infty} f(at)e^{-st} \dd{t}}\) and \({\displaystyle F(s) = \int_0^{\infty} f(t)e^{-st} \dd{t}}\)
Make the substitution \(u = at\), then \(\dd{u} = a \dd{t}\):
\({\displaystyle G(s) = \int_0^{\infty} f(u) e^{-s u/a} \frac{\dd{u}}{a} = \frac{1}{a} \int_0^{\infty} f(u) e^{-(s/a)u} \dd{u} = \frac{1}{a} F(\frac{s}{a})}\)
41 Show that if \(h(t) = f(t) * g(t)\) then \(H(s) = F(s)G(s)\)
41.1 Front
Show that if $h(t) = f(t) * g(t)$ then $H(s) = F(s)G(s)$
Tip: \({\displaystyle F(s) = \int_0^{\infty} f(x)e^{-sx} \dd{x}}\) and \({\displaystyle G(s) = \int_0^{\infty} g(y) e^{-sy} \dd{y}}\); expressing the product as a double integral; and changing coordinates using \(x = t - \tau\), \(y = \tau\)
41.2 Back
\({\displaystyle F(s)G(s) = \int_0^{\infty} \int_0^{\infty} f(x) e^{-sx} g(y)e^{-sy} \dd{x} \dd{y} = \iint_R f(x) g(y) e^{-s(x+y)} \dd{x}\dd{y}}\)
Where \(R\) is the first quadrant. We can use the substitution \(x = t -\tau\), \(y = \tau\). To convert to these coordinates, note that the Jacobian
\({\displaystyle \begin{vmatrix} \pdv{x}{t} & \pdv{x}{\tau} \ \pdv{y}{t} & \pdv{y}{\tau} \end{vmatrix} = \begin{vmatrix} 1 & -1 \ 0 & 1 \end{vmatrix} = 1}\)
For fixed \(t\), \(\tau\) ranges over numbers between \(0\) and \(t\), and \(t\) ranges over positive numbers. Since \(t = x + y\)
\begin{align*} F(s)G(s) &= \int_0^{\infty} \int_0^t f(t - \tau)g(\tau) e^{-st} \dd{\tau} \dd{\tau} \\\ &= \int_0^{\infty} \biggl(\int_0^{\infty} f(t - \tau)g(\tau) \dd{\tau} \biggr) e^{-st} \dd{t} \\\ &= \int_0^{\infty} (f(t) * g(t)) e^{-st} \dd{t} \\\ &= \int_0^{\infty} h(t)e^{-st}\dd{t}\\\ &= H(s) \end{align*}
42 Using the integral definition find the Laplace transform of the \(f(t)\)
42.1 Front
Using the integral definition find the Laplace transform of the $f(t)$
\({\displaystyle f(t) = \begin{cases} 1 &\text{for } 0 \lt t \lt 1 \\\ 0 &\text{for } t \gt 1 \end{cases} }\)
42.2 Back
\({\displaystyle F(s) = \int_0^{\infty} f(t) e^{-st} \dd{t} = \int_0^1 1 e^{-st} \dd{t} + \int_1^{\infty} 0 e^{-st} \dd{t}}\)
This improper integral converges for any \(s\); the region of convergence is the whole complex plane.
\({\displaystyle F(s) = \frac{1}{-s}e^{-st} \bigg|_0^1 = \frac{1 - e^{-s}}{s}}\)