- Captured On
- Source
- Convolution | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is the definition of the convolution of 2 functions?
1.1 Front
What is the definition of the convolution of 2 functions?
One-sided convolution
1.2 Back
It’s a function defined by this integral
\({\displaystyle (f * g)(t) = \int_{0^-}^{t^+} f(\tau) g(t - \tau) \dd{\tau}}\) for \(t \gt 0\)
One-sided convolution is only concerned with functions on the interval \((0^-, \infty)\). When using convolution we never look at \(t \lt 0\)
2 When can we use \(0\) and \(t\) as limits on the convolution function?
2.1 Front
When can we use $0$ and $t$ as limits on the convolution function?
2.2 Back
When both function \(f\) and \(g\) are continuous or have at worst jump discontinuities then we can use \(0\) and \(t\) for the limits.
\({\displaystyle f * g(t) = \int_0^t f(\tau)g(t - \tau) \dd{\tau}}\)
3 Show this equation
3.1 Front
Show this equation
\({\displaystyle e^{at} * e^{bt} = \frac{e^{at} - e^{bt}}{a - b}}\) when \(a \neq b\)
3.2 Back
\begin{align*} e^{at} * e^{bt} &= \int_0^t e^{a\tau} e^{b(t - \tau)} \dd{\tau} \\\ &= e^{bt} \int_0^t e^{(a - b)\tau} \dd{\tau} \\\ &= e^{bt} \frac{e^{(a-b)\tau}}{a - b} \bigg|_0^t \\\ &= e^{bt} \frac{e^{(a-b)t} - 1}{a -b}\\\ &= \frac{e^{at} - e^{bt}}{a - b} \end{align*}
You could safely integrate just from \(0\) to \(t\) instead of having to specify precisely \(0^-\) to \(t^+\)
4 Compute the convolution of this 2 functions
4.1 Front
Compute the convolution of this 2 functions
\({\displaystyle e^{at} * e^{at}}\)
4.2 Back
\begin{align*} e^{at} * e^{at} &= \int_0^t e^{a\tau} e^{a(t - \tau)} \dd{\tau} \\\ &= e^{at} \int_0^t e^{a\tau} e^{-a\tau} \dd{\tau} \\\ &= e^{at} \int_0^t \dd{\tau}\\\ &= e^{at} t \end{align*}
5 Express as a convolution the solution to the first order constant coefficient linear IVP
5.1 Front
Express as a convolution the solution to the first order constant coefficient linear IVP
\(\dot{y} + ky = q(t)\), \(y(0) = 0\)
Don’t use Green’s Theorem for DE. Explain how to reach the integral convolution
We know that \(e^{-kt}\) is the solution to corresponding homogeneous DE \(\dot{y} + ky\), but the initial condition \(y(0) = 1\). This is the simplest case of Green’s Formula.
5.2 Back
Multiplying both sides by its integrating factor \(e^{kt}\)
\({\displaystyle (y e^{kt})’ = q(t) e^{kt}}\)
Integrate both sides from \(0\) to \(t\), and apply the Fundamental Theorem of Calculus to the left side; since we have \(y(0) = 0\), the solution we seek satisfies
\({\displaystyle y_p e^{kt} = \int_0^t q(\tau) e^{k\tau} \dd{\tau}}\)
\({\displaystyle y_p = \int_0^t q(\tau) e^{-k(t - \tau)} \dd{\tau} = q(t) * e^{-kt}}\)
6 Which are the properties of the convolution of 2 functions?
6.1 Front
Which are the properties of the convolution of 2 functions?
6.2 Back
- Linearity (or distributive law)
- \((c_1 f_1 + c_2 f_2) * g = c_1(f_1 * g) + c_2 (f_2 * g)\)
- Commutativity
- \(f * g = g * f\)
- Associativity
- \(f * (g * h) = (f * g) * h\)
- Multiplicative identify (thinking as type of multiplications)
- \(\delta(t)\)
- \((\delta * f)(t) = f(t)\)
7 What is the equivalent to this expression?
7.1 Front
What is the equivalent to this expression?
\({\displaystyle (\delta * f)(t)}\)
7.2 Back
\({\displaystyle (\delta * f)(t) = \int_{0^-}^t \delta(\tau) f (t - \tau) \dd{\tau} = f (t - 0) = f(t)}\)
for \(t \geq 0\)
8 What is the equivalent to this expression?
8.1 Front
What is the equivalent to this expression?
\({\displaystyle (\delta(t - a) * f)(t)}\)
8.2 Back
\({\displaystyle (\delta(t - a) * f)(t) = \int_{0^-}^{t^+} \delta(\tau - a) f(t - \tau) \dd{\tau} = f(t - a) \int_{0^-}^{t^+} \delta(\tau - a) \dd{\tau} = f(t - a)}\)
Checking that \(f(t)\delta(t - a) = f(a) \delta(t - a)\)
For \(t \geq a\), the integral in this expression is just 1, and for \(0 \lt t \lt a\), this integral is zero
9 What is the value of this integral?
9.1 Front
What is the value of this integral?
\({\displaystyle \int_{0^-}^b \delta(\tau) f(\tau) \dd{\tau}}\)
9.2 Back
\(f(0)\)
10 What is the value of the convolution of these 2 functions?
10.1 Front
What is the value of the convolution of these 2 functions?
\({\displaystyle f(t) * 1}\)
10.2 Back
\({\displaystyle f(t) * 1 = \int_0^t f(\tau) 1 \dd{\tau} = \int_0^t f(\tau) \dd{\tau}}\)
11 What is the Green’s Formula for DE?
11.1 Front
What is the Green’s Formula for DE?
11.2 Back
Suppose that we have a linear time invariant system with rest IC
\({\displaystyle p(D) y = f(t)}\), \(y(t) = 0\) for \(t<0\)
We will consider \(f(t)\) to be the input to this system. We don’t consider functions for \(t \lt 0\), the initial conditions mean that \(y(t)\) and all its derivatives are \(0\) at \(t = 0^-\)
Suppose further that \(w(t)\) is the unit impulse response for \(p(D)\). That is, \(w(t)\) satisfies \(p(d) w = \delta(t)\), with rest IC. Then, for any input \(f(t)\) the solution to equation \(p(D) y = f(t)\) is given by Green’s formula
\({\displaystyle y(t) = (f * w)(t) = \int_{0^-}^{t^+} f(\tau) w(t - \tau) \dd{\tau}}\)
12 Why is really useful Green’s formula for DE?
12.1 Front
Why is really useful Green’s formula for DE?
12.2 Back
It tells us the response to any input once we know the unit impulse response. Furthermore, it gives us that response as an integral which can be computed numerically if necessary.
For many physical systems the impulse response can be measured directly or deduced from measurements.
This formula gives us a method for predicting the system’s response to any input.
13 Which are the condition for use the Green’s formula for DE?
13.1 Front
Which are the condition for use the Green’s formula for DE?
13.2 Back
- Have a linear time invariant (LTI) system
- With rest initial conditions
- Know the unit impulse response
14 What is the weight function of a system?
14.1 Front
What is the weight function of a system?
14.2 Back
It’s the unit impulse response
If we think of an integral as a ‘sum’ then Green’s formula shows the solution \(y(t)\) to \(p(D)y = f(t)\) is given as a weighted sum of the small bits of input, \(f(\tau) \dd{\tau}\)
15 Find the particular solution given by Green’s formula to this DE?
15.1 Front
Find the particular solution given by Green’s formula to this DE?
\(\ddot{y} + y = A\), \(y(0) = 0\), \(\dot{y}(0) = 0\), where \(A\) is a constant
Tip: unit impulse response \(w(t) = \sin(t)\)
15.2 Back
For \(t \geq 0\)
\({\displaystyle y_p(t) = \int_0^t A \sin(t - \tau) \dd{\tau} = A \cos(t - \tau) \bigg|_0^t = A (1 - \cos(t))}\)
16 How could we proof the Green’s Formula for DE?
16.1 Front
How could we proof the Green’s Formula for DE?
For \(P(D) y = f(t)\), \(y(t) = 0\) for \(t \lt 0\)
The solution for \(t \gt 0\) is given by
\({\displaystyle y(t) = (f * w)(f) = \int_{0^-}^{t^+} f(\tau) g(t - \tau) \dd{\tau}}\)
where \(w(t)\) is the weight function for the system.
Suppose that \(f(t)\) is continuous
16.2 Back
We will use
- Linear time invariant (LTI) of the system
- Superposition
- Definition of the integral as a limit of Riemman sum
As \(f(t)\) is continuous we can change limits of sum, but this proof work for \(f(t)\) hat has jump discontinuities or contains delta functions
LTI means: \(y(t)\) solves \(P(D)y = f(t) \implies y(t -a)\) solves \(P(D)y = f(t-a)\). We can say that if \(y(t)\) is the response to input \(f(t)\) then \(y(t -a)\) is the response to input \(f(t - a)\)
Divide up time into intervals of width \(\Delta t\). So, \(t_0 = 0, t_1 = \Delta t, t_2 = 2 \Delta t\)
We decompose the input signal \(f(t)\) into packets over each interval. The \(k\text{th}\) signal packet, \(f_k(t)\) coincides with \(f(t)\) between \(t_k\) and \(t_{k+1}\) and \(0\) elsewhere
\({\displaystyle f_k(t) = \begin{cases} f(t) &\text{for } t_k \lt t \lt t_{k+1} \\\ 0 &\text{elsewhere} \end{cases} }\)
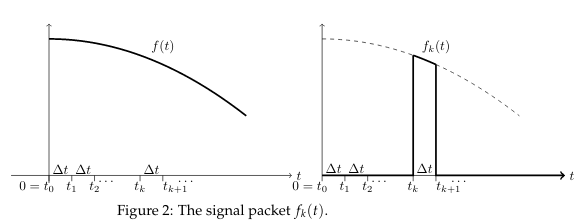
It is clear that for \(t \gt 0\) we have \(f(t)\) is the sum of the packets
\({\displaystyle f(t) = f_0(t) + f_1(t) + \dots + f_k(t) + \dots}\)
A single package \(f_k(t)\) is concentrated entirely in a small neighbourhood of \(t_k\) so it is approximately an impulse with the same size as the area under \(f_k(t)\). The are under \(f_k (t) \approx f(t_k) \Delta t\). Hence,
\({\displaystyle f_k (t) \approx (f(t_k) \Delta t) \delta(t - t_k)}\)
The weight function \(w(t)\) is response to \(\delta(t)\). So, by linear time invariance the response to \(f_k(t)\) is
\({\displaystyle y_{k}(t) \approx (f(t_k) \Delta t) w(t - t_k)}\)
We want to find the response at a fixed time. Since \(t\) is already in use, we will let \(T\) be our fixed time and find \(y(T)\)
Since \(f\) is the sum of \(f_k\), superposition gives \(y\) is the sum of \(y_k\).
\({\displaystyle y(T) = y_o(T) + y_1(T) + \dots \approx \biggl(f(t_0) w(T - t_0) + f(t_1)w(T - t_1) + \dots \biggr) \Delta t}\)
We can ignore all the terms where \(t_k > T\) (Because then \(w(T - t_k) = 0\), since \(T - t_k \lt 0\)). If \(n\) is the last index where \(t_k \lt T\)
\({\displaystyle y(T) \approx \biggl(f(t_0)w(T - t_0) + f(t_1)w(T - t_1) + \dots f(t_n)w(T - t_n) \biggr)\Delta t}\)
This is the Riemann sum and as \(\Delta t \to 0\) it goes to an integral
\({\displaystyle y(T) = \int_0^T f(t)w(T - t) \dd{t}}\)
17 What is the causality principle?
17.1 Front
What is the causality principle?
Why is it important for system?
17.2 Back
Causality is the principle that the future does not affect the past. Green’s theorem shows that the system \(p(D)y = f(t)\) where \(y(t) = 0\) for \(t \lt 0\) is causal.
That means \(y(t)\) only depends on the input up to time \(t\).
Real physical system are causal
18 Describe non-causal systems
18.1 Front
Describe non-causal systems
18.2 Back
An audio compressor that gathers information after time \(t\) before deciding how to compress the signal at time \(t\).
System with input \(f(t)\) and output \(y(t)\) where \(y\) is the solution to \(\dot{y} = f(t + 1)\)
19 How much is in the lake at time \(t > 0\)?
19.1 Front
How much is in the lake at time $t > 0$?
We have a lake, and a pollutant is being dumped into it, at a certain variable rate \(f(t)\). This pollutant degrades exponentially over time. If the lake begins at time zero with no pollutant, how much is in the lake at time \(t \gt 0\)?
Don’t use Green’s Formula. Tip: Use the exponential decay
19.2 Back
Let \(x(t)\) be the amount of pollutant in the lake at time \(t\), and \(a\) be the decay constant.
For exponential decay we know that if a quantity of \(p\) of pollutant is dropped in the lake at time \(\tau_k\) then at a later time \(t\) (\(t > \tau_k\)) it will have been reduced to the amount \({\displaystyle pe^{-a(t - \tau_k)}}\)
\(t - \tau_k\) is the time elapsed between when the pollutant is added and when we check how much of it is left
In our system pollutant is not being added all at once. Rather, it is dripping continuously into the lake
We break the interval \([0, t]\) into \(n\) small pieces of width \(\Delta \tau\)
Let \(p_k\) be the amount of pollutant added in the interval \([\tau_k, \tau_{k+1}]\)
Since \(\Delta \tau\) is small we get the approximation \(p_k \approx f(\tau_k) \Delta \tau\). Remember \(f(\tau)\) is a rate, so multiplying by time we get amount
So, the amount of this left at time \(t\) is approximately, that is the contribution to \(x(t)\) from the interval \([\tau_k, \tau_{k + 1}]\)
\({\displaystyle p_k e^{-a (t - \tau_k)} \approx f(\tau_k) \Delta \tau e^{-a (t - \tau_k)}}\)
So, \(x(t)\) it is the sum up of the contributions of all the intervals
\begin{align*} x(t) &\approx p_0 e^{-a (t - \tau_0)} + p_1 e^{-a (t - \tau_1)} + \dots + p_0 e^{-a (t - \tau_0)} \\\ &\approx \biggl( f(\tau_0) e^{-a(t - \tau_0)} + f(\tau_1) e^{-a(t - \tau_1)} + \dots f(\tau_n) e^{-a(t - \tau_n)} \biggr) \Delta \tau \end{align*}
This is a Riemann sum taking the limit as \(\Delta \tau \to 0\) we get the convolution integral
\({\displaystyle x(t) = \int_0^t f(\tau)e^{-a(t - \tau)} \dd{\tau}}\)
20 What is the response to this system using Green’s formula?
20.1 Front
What is the response to this system using Green’s formula?
\({\displaystyle 2 \ddot{x} + 8 x = \cos(2t)}\), with rest IC
20.2 Back
For \(t > 0\), the weight function is the solution to
\(2 \ddot{w} + 8 w = 0\), \(w(0) = 0\), \(\dot{w}(0) = 1/2\)
The solution is \({\displaystyle w(t) = \frac{1}{4} \sin(2t)}\)
For \(t > 0\) Green’s formula gives
\({\displaystyle x(t) = \int_0^t \sin(2\tau) \frac{1}{4} \cos(2 (t - \tau)) \dd{\tau}}\)
Using the trigonometric identity:
\({\displaystyle \sin(A) \cos(B) = \frac{\sin(A + B) + \sin(A - B)}{2}}\)
\begin{align*} x(t) &= \int_0^t \sin(2\tau) \frac{1}{4} \cos(2(t - \tau)) \dd{\tau} \\\ &= \frac{1}{8} \int_0^t (\sin(2t) + \sin(4\tau - 2t)) \dd{\tau} \\\ &= \frac{1}{8} \biggl( \tau \sin(2t) - \frac{\cos(4\tau - 2t)}{4} \biggr|_0^t \\\ &= \frac{t \sin(2t)}{8} \end{align*}
This is the answer we expected from our earlier work with the exponential response formula