- Captured On
- Source
- Unit Step and Unit Impulse Response | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare
In this session we study differential equations with step or delta functions as input. For physical systems, this means that we are looking at discontinuous or impulsive inputs to the system.
1 When happens the pre-initial conditions in a DE?
1.1 Front
When happens the pre-initial conditions in a DE?
1.2 Back
\(x(0^-)\), \(\dot{x}(0^-)\)
2 When happens the post-initial conditions in a DE?
2.1 Front
When happens the post-initial conditions in a DE?
2.2 Back
\(x(0^+)\), \(\dot{x}(0^+)\)
3 When are pre-initial and post-initials conditions of a DE necessary?
3.1 Front
When are pre-initial and post-initials conditions of a DE necessary?
3.2 Back
When there is a discontinuity at \(t=0\) in the input signal of the DE. Sometimes, if we say initial conditions we will mean the pre-initial conditions.
If \(x(t)\) is smooth the pre and post-initial conditions are the same and their is no need to distinguish between them.
4 What is the solution for this equation?
4.1 Front
What is the solution for this equation?
\(\dot{x} = u(t)\), \(x(0^-) = 0\)
Explain the initial conditions values
4.2 Back
\({\displaystyle x(t) = \begin{cases} 0 &\text{for } t \lt 0 \\\ t &\text{for } t \gt 0 \end{cases} }\)
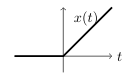
- \(x(0^+) = 0\), the post-initial condition is equals to pre-initial condition
- Rate of change jumps from 0 to 1 \(\dot{x} = u(t)\) at \(t=0\)
- So, the response \(x(t)\) should be continuous
- \(\dot{x}(0^-) = 0 \neq \dot{x}(0^+) = 1\)
5 What is the solution for this DE?
5.1 Front
What is the solution for this DE?
\(\dot{x} = \delta(t)\), \(x(0^-) = 0\)
Explain the initial conditions values
5.2 Back
- Integrating \(\delta(t)\), \(x(t) = u(t)\)
- Pre-initial conditions is different to post-initial condition
- \(x(0^-) = 0 \neq x(0^+) = 1\)
- The impulse causes a jump in the value of \(x\)
6 What is the solution for this DE?
6.1 Front
What is the solution for this DE?
\(\ddot{x} = u(t)\), \(x(0^-) = 0\), \(\dot{x}(0^-) = 0\)
6.2 Back
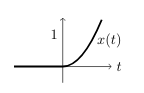
- Integrating twice
- \({\displaystyle x(t) = \begin{cases} 0 &\text{for } t \lt 0 \\\ t^2/2 &\text{for } t \gt 0 \end{cases} }\)
- \(x(0^-) = x(0^+) = 0\)
- \(\dot{x}(0^-) = \dot{x}(0^+) = 0\)
- \(\ddot{x}(0^-) = 0 \neq \ddot{x}(0^+) = 1\)
7 What is the solution for this DE?
7.1 Front
What is the solution for this DE?
\(\ddot{x} = \delta(t)\), \(x(0^-) = 0\), \(\dot{x}(0^-) = 0\)
Explain initial value conditions
7.2 Back
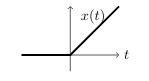
- \({\displaystyle x(t) = \begin{cases} 0 &\text{for } t \lt 0\\\ t &\text{for } t \gt 0 \end{cases} }\)
- \(x(0^-) = x(0^+) = 0\)
- \(\dot{x}(0^-) = 0 \neq x(0^+) = 1\)
In this cases \(x(t)\) itself is continuous, but for the second order equation the input \(\delta(t)\) caused a jump in the first derivative
8 What are the rest initial conditions?
8.1 Front
What are the rest initial conditions?
Explain the case for DE of order \(n\)
8.2 Back
Is the case where \(x(t) = 0\) for \(t \lt 0\)
\({\displaystyle x(0^-) = 0, \dot{x}(0^-) = 0, \dots, x^{(n-1)}(0^-) = 0}\)
9 What happens to the response and initial conditions of DE with unit step input?
9.1 Front
What happens to the response and initial conditions of DE with unit step input?
9.2 Back
It causes a smooth response with matching pre and post-initial conditions
10 What happens to the response and initial conditions of DE with unit impulse input?
10.1 Front
What happens to the response and initial conditions of DE with unit impulse input?
10.2 Back
The response could contains jumps or be continuous. It’s a piecewise smooth functions.
The pre and post initial conditions match except for the derivative one less than the order of the equation.
11 What would be the model of this DE?
11.1 Front
What would be the model of this DE?
\({\displaystyle \dot{x} + kx = ru(t)}\), \(x(0^-) = 0\), where \(k,r\) are constants
Tip: Nuclear reactor
11.2 Back
This would model the amount of uranium in a nuclear reactor where we add uranium at the constant rate of \(r\) kg/year starting at time \(t=0\) and where \(k\) is the decay rate of the uranium.
12 How could we solve this DE?
12.1 Front
How could we solve this DE?
\({\displaystyle \dot{x} + kx = ru(t)}\), \(x(0^-) = 0\) where \(r,k\) are constants
Don’t assume that the response must be continuous because of unit step input
12.2 Back
The equation is \({\displaystyle \dot{x} + kx = \begin{cases} 0 &\text{for } t \lt 0 \ r &\text{for } t \gt 0 \end{cases} }\)
Solving the 2 pieces, we get \({\displaystyle x(t) = \begin{cases} c_1e^{-kt} &\text{for } t \lt 0 \ r/k + c_2e^{-kt} &\text{for } t \gt 0 \end{cases} }\)
This gives \(x(0^-) = c_1\) and \(x(0^+) = r/k + c_2\). If these two are different there is a jump at \(t=0\) of magnitude \(x(0^-) - x(0^+) = r/k + c_2 - c_1\)
As \(x(0^-) = 0\), implies \(c_1 = 0\), our solution looks like \({\displaystyle x(t) = \begin{cases} 0 &\text{for } t \lt 0\ r/k + c_2e^{-kt} &\text{for } t \gt 0 \end{cases} }\)
Substituting this into our differential equation, where we must use the generalized derivative if there is a jump at \(t=0\)
\begin{align*} \dot{x} + kx &= (r/k + c_2)\delta(t) + \begin{cases} 0 &\text{for } t \lt 0\ -k c_2 e^{-kt} + r + kc_2 e^{-kt} &\text{for } t \gt 0 \end{cases} \\\ &= (r/k +c_2 )\delta(t) + \begin{cases} 0 &\text{for } t \lt 0\\\ r &\text{for } t \gt 0 \end{cases} \end{align*}
Comparing the RHS, we see that \(r/k + c_2 = 0 \implies c_2 = -r/k\)
So the solution is
\({\displaystyle x(t) = \begin{cases} 0 &\text{for } t \lt 0 \ r/k(1 - e^{-kt}) &\text{for } t \gt 0 \end{cases} }\)
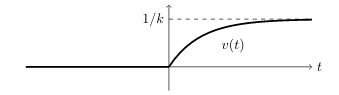
13 What does mean the phrase ‘Unit Step Response’?
13.1 Front
What does mean the phrase ‘Unit Step Response’?
For this system, \(\dot{x} + kx = f(t)\)
13.2 Back
The unit step response means the response of the system when the input is a unit step.
We consider \(f(t)\) to be the input. But sometimes makes more sense to consider something else to be the input. For example, in Newton’s law of cooling \(\dot{T} + kT = k T_e\) it makes physical sense to call \(T_e\) the temperature of the environment, the input.
In this case the unit step response of the system means the response to the input \(T_e(t) = u(t)\), the solution to \(\dot{T} + kT = ku(t)\)
It’s written \(v(t)\)
14 For the solution \(v(t)\) what is \(\dot{v}(0^{+})\)?
14.1 Front
For the solution $v(t)$ what is $\dot{v}(0^{+})$?
Consider the equation \(\dot{v} + kv = u(t)\) with rest initial conditions, \(v(0^-) = 0\)
14.2 Back
\(v(t)\) is continuous so \(v(0^-) = v(0^+) = v(0) = 0\). Therefore the DE shows \(\dot{v}(0^+) = u(0^+) = 1\)
15 What would be the model of this DE?
15.1 Front
What would be the model of this DE?
\({\displaystyle \dot{x} + kx = \delta(t)}\), \(x(0^-) = 0\), where \(k,r\) are constants
Tip: Nuclear reactor
15.2 Back
This would model, the amount of uranium in a nuclear reactor where at \(t=0\) we add \(1\) kg of uranium all at once and \(k\) is the decay rate of the uranium
16 How could we solve this DE?
16.1 Front
How could we solve this DE?
\({\displaystyle \dot{x} + kx = \delta(t)}\), \(x(0^-) = 0\), where \(k,r\) are constants
16.2 Back
Because of the rest initial conditions we have \(x(t) = 0\) for \(t \lt 0\)
The effect of the input is to cause the amount \(x(t)\) to jump from \(0\) to \(1\) at \(t = 0\). That is, \(x(0^+) = 1\). For \(t>0\) the input \(\delta(t) = 0\) and,
Therefore, for \(t > 0\) we should solve \(\dot{x} + kx = 0\), \(x(0) = 1\), which general solution is \(x(t) = ce^{-kt}\). Using \(x(0) = 1 \implies c=1\)
\({\displaystyle x(t) = e^{-kt} u(t) = \begin{cases} 0 &\text{for } t \lt 0\\\ e^{-kt} &\text{for } t \gt 0 \end{cases}}\)
17 What is the unit impulse response?
17.1 Front
What is the unit impulse response?
17.2 Back
We denote \(w(t)\). In some sense it is the simplest nontrivial solution to the system \(\dot{x} + kx = \delta(t)\), \(x(0^-) = 0\), where \(k\) is constant
\(w(t) = u(t) e^{-kt}\)
You just give the system a unit kick at \(t=0\), stand back, and watch the result.
For \(t \gt 0\) it is just the homogeneous solution with initial condition \(x(0) = 1\)
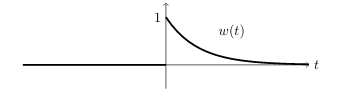
18 Which is the graph of the unit impulse response?
18.1 Front
Which is the graph of the unit impulse response?
\(w(t) = u(t) e^{-kt}\)
18.2 Back
At \(t=0\) it jumps to \(x=1\) and then decays exponentially to \(0\)
19 How is the response if you use the box function instead of \(\delta(t)\) as input?
19.1 Front
How is the response if you use the box function instead of $\delta(t)$ as input?
\(\dot{x} + kx = q(t)\)
Don’t solve it using \({\displaystyle u_h = \begin{cases} 0 &\text{for } t \lt 0 \ 1/h &\text{for } 0 \lt t \lt h \ 0 &\text{for } h \lt t \end{cases} }\)
Only graph an sketch for several \(h\)
19.2 Back
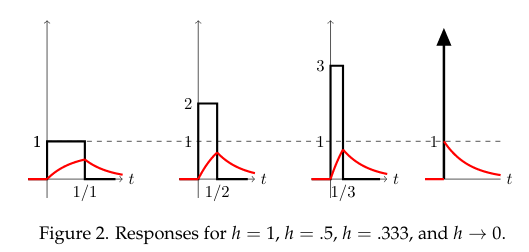
The input is plotted in black and the output in red. Notice how the output rises faster and gets closer to \(1\) as \(h \to 0\). Finally, in the limit of small \(h\), it jumps directly to \(1\)
20 What does mean the phrase ‘Unit Impulse Response’?
20.1 Front
What does mean the phrase ‘Unit Impulse Response’?
For: \({\displaystyle \dot{x} + kx = f(t)}\)
20.2 Back
The unit impulse response means the response of the system when the input is a unit impulse.
We considered \(f(t)\) to be the input. Suppose, instead, we have the system \({\displaystyle \dot{T} + k T = k T_e}\), we consider \(T_e\) to be the input.
Then, the unit impulse response is the response of the system to input \(T_e(t) = \delta(t)\), i.e. the solution to \({\displaystyle \dot{T} + kT = k \delta(t)}\)
21 For the solution \(w(t)\) what is \(\dot{w}(0^+)\)?
21.1 Front
For the solution $w(t)$ what is $\dot{w}(0^{+})$?
Consider the equation \({\displaystyle \dot{w}(t) + kw = \delta(t)}\) with rest initial conditions, \(w(0^-) = 0\)
21.2 Back
Using the DE we get \(\dot{w}(0^+) + k w(0^+) = \delta(0^+)\). We know \(w(0^+) = 1\) and \(\delta(0^+) = 0\). Therefore \(\dot{w}(0^+) = -k\)
We could also look at the solution \(w(t) = e^{-kt}\) for \(t > 0\). Thus \(\dot{w}(t) = -k e^{-kt}\) for \(t>0\). This implies \(\dot{w}(0^+) = -k\)
Using the solution to the DE probably seems easier than the first method, but it is important to be able to draw conclusions without knowing the solution.
22 What is the solution for this DE?
22.1 Front
What is the solution for this DE?
\(m \ddot{x} + kx = u(t)\), where \(x(0^-) = 0\), \(\dot{x}(0^-) = 0\)
You can use continuity response assumption, but you must explain it
22.2 Back
The mass is at res at equilibrium until \(t = 0\) when a steady force starts to acts on it.
Force represents a change in momentum over time. A finite force \(F(t)\) can only cause and infinitesimal change in momentum (i.e. \(F(t) \dd{t}\)) at a time. Therefore, the mass does not change position abruptly, nor does it change velocity instantaneously. Because of this we should expect a solution which is continuous with continuous derivative. Only the acceleration experiences a discontinuity.
For \(t < 0\), we already know that \(x(t) = 0\). For \(t>0\) the DE is \(m \ddot{x} + kx = 1\). Which solution is \(x(t) = x_p(t) + x_h(t)\)
- \({\displaystyle x_p(t) = \frac{1}{k}}\)
- \({\displaystyle x_h(t) = c_1 \cos(\omega_n t) + c_2 \sin(\omega_n t)}\), where \({\displaystyle \omega_n = \sqrt{\frac{k}{m}}}\)
The continuity of \(x\) and \(\ddot{x}\) implies \(x(0) = x(0^-) = 0\), and \(\dot{x}(0) = \dot{x}(0^-) = 0\). This allow us to find \(c_1\) and \(c_2\)
- \(0 = x(0) = 1/k + c_1 \implies c_1 = - 1/k\)
- \(0 = \dot{x}(0) = c_2 \omega_n \implies c_2 = 0\)
The unit step response for this system is
\({\displaystyle x(t) = \frac{1}{k} (1 - \cos(\omega_n t)) u(t) = v(t)}\)
You can solve it without assume this continuity in the response, you need to solve for the different cases \(t \lt 0\) and \(t \gt 0\), replace IVP pre-initials conditions, substitute the solution in the DE and compare with the RHS of the DE.
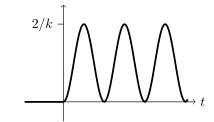
23 How is the graph of the unit step response?
23.1 Front
How is the graph of the unit step response?
DE: \(m \ddot{x} + kx = u(t)\)
Draw and sketch
23.2 Back
24 Meaning of the ‘Unit Step Response’
24.1 Front
Meaning of the ‘Unit Step Response’
\(m \ddot{x} + b \dot{x} + kx = b \dot{y}\), consider \(y\) to be the unit step input
24.2 Back
The unit step response is the response of the system to a unit step input. The unit step response for these systems are equivalents
- \(m \ddot{x} + b \dot{x} + kx = b \dot{u}(t)\)
- \(m \ddot{x} + b \dot{x} + kx = b \delta(t)\)
25 Which are the properties of this system’s response?
25.1 Front
Which are the properties of this system’s response?
\(m \ddot{x} + b \dot{x} + kx = f(t)\), where the input is \(f(t) = c \delta(t - a)\)
How are \(x(t)\) and \(\dot{x}(t)\)?
25.2 Back
- The momentum \(m \dot{x}(t)\) jumps by \(c\) units at \(t = a\), that is
\({\displaystyle m \dot{x}(a^+) - m \dot{x}(a^-) = c}\)
- \(\dot{x}(a^+) = c / m\) if \(\dot{x}(a^-) = 0\)
- The position \(x(t)\) is unchanged at \(t = a\), that is \(x(a^+) = x(a^-)\)
26 Why the position \(x(t)\) is unchanged at \(t=a\) for this DE?
26.1 Front
Why the position $x(t)$ is unchanged at $t=a$ for this DE?
\(m \ddot{x} + b \dot{x} + kx = f(t)\) where \(f(t) = c \delta(t-a)\)
26.2 Back
If \(x(t)\) had a jump at \(t = a\) then \(\dot{x}\) would contain a multiple of \(\delta(t - a)\). So, \(m \ddot{x}\) would contain a multiple of the doublet \(\delta’(t-a)\). This is impossible since the input \(\delta(t-a)\) does not contain a doublet
So, \(x(a^-) = x(a^+)\)
27 Why are there a jump of \(c\) units in \(m \dot{x}\) term in this DE?
27.1 Front
Why are there a jump of $c$ units in $m \dot{x}$ term in this DE?
\(m \ddot{x} + b \dot{x} + k x = f(t)\) where \(f(t) = c \delta(t - a)\)
27.2 Back
To make the left-hand side of equation match the right hand side, \(m \dot{x}(t)\) has a jump of \(c\) units at \(t = a\), so \(m \ddot{x}(t)\) contains the term \(c \delta (t - a)\)
28 What is the unit impulse response for this system?
28.1 Front
What is the unit impulse response for this system?
\({\displaystyle m \ddot{x} + b \dot{x} + kx = f(t)}\), only set up the conditions for solving it
Write its equivalent ODE
28.2 Back
Is the solution to this equation with input \(f(t) = \delta(t)\) and rest initial conditions: \(x(t) = 0\) for \(t < 0\). So the IVP are \(x(0^-) = 0\) and \(\dot{x}(0^-) = 0\)
Let \(w(t)\) denote the solution we seek. The unit impulse input will cause a unit jump in the momentum at \(t = 0\) and no change in position. We also know that, for \(t > 0\), the input \(\delta(t) = 0\). So for \(t > 0\), \(w(t)\) satisfies the equation
\(m \ddot{w} + b \dot{w} + kw = 0\), where \(\dot{w}(0^+) = 1/m\) and \(w(0^+) = 0\)
You will get it, solving this DE
29 Describe how would be a system with this DE?
29.1 Front
Describe how would be a system with this DE?
\(m \ddot{x} + b \dot{x} + kx = \delta (t)\) with rest conditions
Describe it with a physical example
29.2 Back
This could be a damped spring-mass system with mass \(m\), damping constant \(b\) and spring constant \(k\). The mass is at rest at equilibrium unit time \(t = 0\) when it is hit by a sudden very brief intense force, rather like getting hit on the head by a hammer. The effect is to increase the momentum instantaneously, without changing the position of the mass
30 Draw a sketch of the unit impulse response for this system
30.1 Front
Draw a sketch of the unit impulse response for this system
\(m \ddot{x} + b \dot{x} + k x = \delta(t)\)
30.2 Back
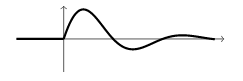
31 What does mean the unit impulse response for this system?
31.1 Front
What does mean the unit impulse response for this system?
\(m \ddot{x} + b \dot{x} + kx = b \dot{y}\)
31.2 Back
It’s the response to this system considering \(y\) as the unit impulse input of the system. So that means the solution to
\(m \ddot{x} + b \dot{x} + kx = b \dot{\delta}(t)\) with rest IC where \(\dot{\delta}(t)\) is a doublet.
For \(t > 0\) this is equivalent to
\({\displaystyle m \ddot{x} + b \dot{x} + kx = 0}\) with post IC \({\displaystyle x(0^+) = \frac{b}{m}}\) and \({\displaystyle x(0^+) = - \frac{b^2}{m^2}}\)
32 What is \(\dot{w}(0^{+})\)?
32.1 Front
What is $\dot{w}(0^{+})$?
Let \(w(t)\) be the solution to \(m \ddot{x} + kx = \delta(t)\) with rest initial conditions
32.2 Back
The unit impulse input causes a unit jump in momentum. Starting from rest this means \(m \dot{w}(0^+) = 1\), so \(\dot{w}(0^+) = 1/m\)
33 What are the post-initial conditions for this system?
33.1 Front
What are the post-initial conditions for this system?
\({\displaystyle a_n x^{(n)} + a_{n-1}x^{(n-1)} + \dots + a_1 x’ + a_0 x = \delta(t)}\) with rest IC
33.2 Back
The effect of the \(\delta\) function input is to cause a jump in the \(n-1^{\text{st}}\) derivative at time \(t = 0\), while the lower order derivatives do not jump.
- \(x(0^+) = 0\)
- \(x’(0^+) = 0\)
- \(\dots\)
- \(x^{(n-2)}(0^+) = 0\)
- \(x^{(n-1)}(0^+) = 1 / a_n\)
Since \(x^{n-1}(t)\) has a jump of \(x^{(n-1)}(0^+) = 1 / a_n\) at \(t = 0\), its derivative \(a_n x^{(n)}(t)\) has a unit impulse, \(\delta(t)\), at \(t = 0\)
34 How could we know the unit impulse response from the unit step response?
34.1 Front
How could we know the unit impulse response from the unit step response?
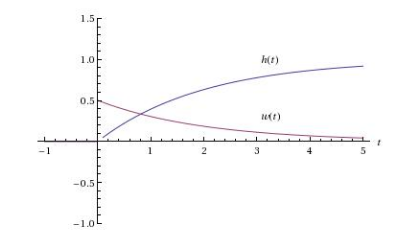
Suppose that \(h(t)\) is the unit step response where \(h(t) = (1 - e^{-t/2}) u(t)\)
Graph both responses
34.2 Back
The unit impulse response is the derivative of the unit step response, so
\({\displaystyle w(t) = h’(t) = \frac{1}{2} e^{-t/2} u(t) + (1 - e^{-t/2}\delta(t)) = \frac{1}{2} e^{-t/2} u(t)}\)
The term \({\displaystyle (1 - e^{-t/2} \delta(t) = 0}\) because at \(t = 0\) the coefficient of \(\delta(t)\) is \(0\)
35 Find the solution for this DE from its unit impulse response
35.1 Front
Find the solution for this DE from its unit impulse response
\({\displaystyle \ddot{x} + 2 \dot{x} = 3\delta(t - 1)}\), where its unit impulse response is \({\displaystyle w(t) = \frac{1}{2}(1 - e^{-2t}) u(t)}\)
35.2 Back
Using time invariance, we find that a solution to this equation is
\({\displaystyle x = 3 w(t-1) = \frac{3}{2}(1 - e^{2 - 2t}) u(t - 1)}\)