This session looks closely at discontinuous functions and introduces the notion of an impulse or delta function. The goal is to use these functions as the input to differential equations. Step functions and delta functions are not differentiable in the usual sense, but they do have what we will call generalized derivatives, which are suitable for use in DE’s.
1 What is a delta function? Write an example with forces
1.1 Front
What is a delta function? Write an example with forces
1.2 Back
A delta function represents an idealized input that acts all at once. If a finite force pushes on a mass it changes the momentum of the mass over time.
We can achieve the same change in momentum with a small force acting over a long time or a large force acting over a short time.
If the force acts over a very shorts time we call it an impulse.
2 What is the unit delta function \(\delta(t)\)?
2.1 Front
What is the unit delta function $\delta(t)$?
2.2 Back
Models an idealized impulse, which can be through of as an infinite force acting over an infinitesimal amount of time and causes a unit change in the momentum of the mass.
It’s also called unit impulse function
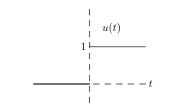
3 What is the Heaviside unit step function?
3.1 Front
What is the Heaviside unit step function?
3.2 Back
The unit function is defined by
\({\displaystyle u(t) =\begin{cases} 0 &\text{for } t \lt 0 \1 & \text{for } t \gt 0\end{cases}}\)
4 How is the graph of this Heaviside unit step function?
4.1 Front
How is the graph of this Heaviside unit step function?
\({\displaystyle u(t - a) =\begin{cases} 0 &\text{for } t \lt a \1 & \text{for } t \gt a\end{cases}}\)
4.2 Back
It’s the function \(u(t)\) shifted to the right
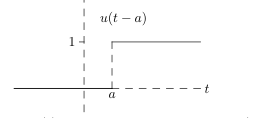
5 What happens to the Heaviside function \(u(t)\) at \(t=0\)?
5.1 Front
What happens to the Heaviside function $u(t)$ at $t=0$?
5.2 Back
\(u(t)\) is not defined at \(t=0\), there is a jump discontinuity in this point
The graph shows that \(u(0^-) = 0\) and \(u(0^+) = 1\)
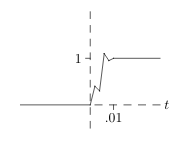
6 How can we model an on / off process? What is really happens?
6.1 Front
How can we model an on / off process? What is really happens?
6.2 Back
We can use the Heaviside function \(u(t)\) as a basic model. But in reality, the light doesn’t reach its steady state instantaneously; it takes a small amount of time.
It might move up smoothly; it might overshoot; it might move up and fits and starts as different elements come on line.
7 How can we model switch on / off / on again?
7.1 Front
How can we model switch on / off / on again?
To be general, let’s assume the light goes on a time \(a\) and off at time \(b\)
7.2 Back
\({\displaystyle u_{ab}(t) = \begin{cases} 0 &\text{for } t \lt a \ 1 &\text{for } a \lt t \lt b \ 0 &\text{for } t \lt a \end{cases}}\)
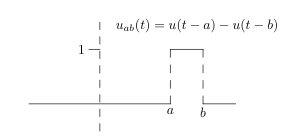
This is called a box function. You can reach the same function with
\({\displaystyle u_{ab}(t) = u(t - a) - u(t - b)}\)
8 Write this box function in terms of Heaviside function?
8.1 Front
Write this box function in terms of Heaviside function?
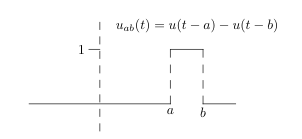
8.2 Back
\({\displaystyle u_{ab}(t) = u(t - a) - u(t - b)}\)
9 How can we switch on / off any function \(f(t)\)?
9.1 Front
How can we switch on / off any function $f(t)$?
9.2 Back
Multiplying \(f(t)\) with a Heaviside function \(u(t)\)
10 Which is the graph of switching on \(f(t)\) at \(t = a\)?
10.1 Front
Which is the graph of switching on $f(t)$ at $t = a$?
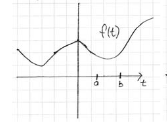
Write also its equation
10.2 Back
Multiplying \(u(t-a) f(t)\), where is \(0\) for \(t \lt a\) and agrees with \(f(t)\) for \(t \gt a\)
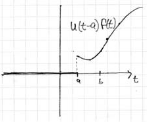
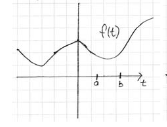
11 How is the graph and equation switching on \(f(t)\)
11.1 Front
How is the graph and equation switching on $f(t)$
for \(a \lt t \lt b\)
11.2 Back
Multiply by the box function, so its equation is \([u(t-a) - u(t-b)] f(t)\). Where \(f(t)\) is on in the window \(a \lt t \lt b\), and off outside.
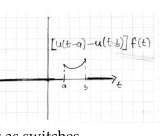
12 Express \(f(t)\) in both \(u\) and cases format
12.1 Front
Express $f(t)$ in both $u$ and cases format
Suppose \(f(t)\) is \(0\) for \(t \lt 0\), \(t\) for \(0 \lt t \lt 1\), \(t^2\) for \(1 \lt t \lt 2\) and \(2t\) for \(t \gt 2\)
12.2 Back
\({\displaystyle f(t) = \begin{cases} 0 &\text{for } t \lt 0 \ t &\text{for } 0 \lt t \lt 1 \ t^2 &\text{for } 1 \lt t \lt 2 \ 2t &\text{for } 2 \lt t \end{cases}}\)
Using \(u-\text{format}\) uses step and box functions to turn on and off expressions
\({\displaystyle f(t) = (u(t) - u(t-1))t + (u(t-1) - u(t-2))t^2 + u(t-2)2t}\)
13 Write this function in cases format
13.1 Front
Write this function in cases format
\({\displaystyle f(t) = u(t)4t + u(t-2)t^2 + u(t-4)t^3/4}\)
13.2 Back
\({\displaystyle f(t) = \begin{cases} 0 &\text{for } t \lt 0 \ 4t &\text{for } 0 \lt t \lt 2 \ 4t + t^2 &\text{for } 2 \lt t \lt 4 \ 4t + t^2 + t^3/4 &\text{for } 4 \lt t \end{cases}}\)
14 What is the model when a radioactive material is dumped in a container?
14.1 Front
What is the model when a radioactive material is dumped in a container?
Write the equation of the amount of material in the tank
Assume 1 kg of material dumped
Explain the complete process to reach the equation
14.2 Back
\({\displaystyle \dot{x} + kx = q(t)}\)
- \(x(t)\) is the amount of radioactive material (in kg)
- \(k\) is the decay rate of the material \(\text{year}^{-1}\)
- \(q(t)\) is the rate at which material is being added to the dump (kg / year)
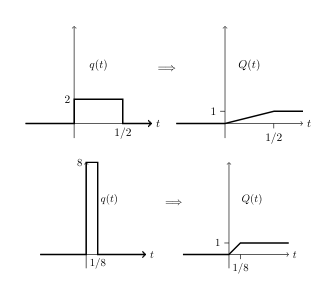
The total of amount dumped into the container from time \(0\) to time \(t\)
\({\displaystyle Q(t) = \int_0^t q(u) du}\), so \({\displaystyle \dot{Q}(t) = q(t)}\)
Assume that \(q(t)\) is only nonzero for a short amount of time and \(Q(t) = \SI{1}{kg}\)
There are multiples possibilities of throw the material, where the amount of dumped material is \(\SI{1}{kg}\)
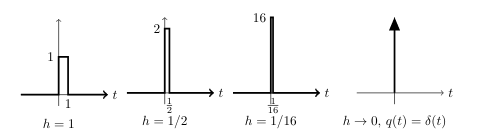
Now, let \(q_h(t)\) be a box of width \(h\) and height \(1/h\). As \(h \to 0\), the width of the box becomes \(0\), the graph looks more and more like a spike, yet it still has area \(1\)
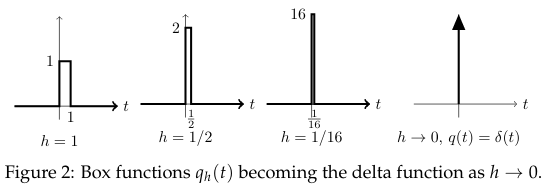
So, its model is
\({\displaystyle \dot{x} + kx = q(t) = \delta(t)}\)
15 What is the value of \(\delta(t)\) at \(t=0\)?
15.1 Front
What is the value of $\delta(t)$ at $t=0$?
\(\delta(0)\)
15.2 Back
\(\infty\)
16 What is the value of \(\delta(t)\) when \(t \neq 0\)?
16.1 Front
What is the value of $\delta(t)$ when $t \neq 0$?
16.2 Back
\(0\)
17 Write the \(\delta(t)\) function in cases format
17.1 Front
Write the $\delta(t)$ function in cases format
\(\delta(t)\)
17.2 Back
\({\displaystyle \delta(t) = \begin{cases} 0 & \text{if } t\neq0\\\ \infty &\text{if } t=0 \end{cases}}\)
18 What is the formal definition of delta function \(\delta(t)\)?
18.1 Front
What is the formal definition of delta function $\delta(t)$?
18.2 Back
Define the box function \({\displaystyle q_h(t) = \begin{cases} 0 &\text{for } t \lt 0 \ 1/h &\text{for } 0 \lt t \lt h \ 0 &\text{for } h \lt t \end{cases} }\)
Where \(q_h(t)\) is a box function of width \(h\) and height \(1/h\).
\({\displaystyle \delta(t) = \lim_{h \to 0} q_h(t) = \delta(t)}\)
19 What represent the delta function \(\delta(t)\) as input function?
19.1 Front
What represent the delta function $\delta(t)$ as input function?
Suppose that is material
19.2 Back
It represents the ideal case where 1 unit of material is dumped in all at once at time \(t=0\)
20 What is the value of this integral?
20.1 Front
What is the value of this integral?
\({\displaystyle \int_c^d \delta(t) \dd{t}}\)
20.2 Back
As \(\delta(t)\) is the limit of graphs of area \(1\), the area under its graph is 1
\({\displaystyle \int_c^d \delta(t) \dd{t} = \begin{cases} 1 & \text{if } c \lt 0 \lt d \\\ 0 & \text{otherwise} \end{cases} }\)
21 What is the value of \(f(t)\delta(t)\) for any continuous \(f(t)\)?
21.1 Front
What is the value of $f(t)\delta(t)$ for any continuous $f(t)$?
21.2 Back
\(f(t)\delta(t) = f(0) \delta(t)\)
22 What is the value of this integral?
22.1 Front
What is the value of this integral?
\({\displaystyle \int_c^d f(t) \delta(t) \dd{t}}\)
22.2 Back
\({\displaystyle \int_c^d f(t) \delta(t) \dd{t} = \begin{cases} f(0) & \text{if } c \lt 0 \lt d \\\ 0 & \text{otherwise} \end{cases} }\)
As \(f(t)\delta(t) = f(0) \delta(t)\)
23 What is the value of this expression?
23.1 Front
What is the value of this expression?
\(f(t)\delta(t-a)\)
23.2 Back
\(f(t)\delta(t-a) = f(a) \delta (t-a)\)
24 What is the value of this integral?
24.1 Front
What is the value of this integral?
\({\displaystyle \int_c^d f(t)\delta(t-a) \dd{t}}\)
24.2 Back
\({\displaystyle \int_c^d f(t)\delta(t-a) \dd{t} = \begin{cases} f(a) & \text{if } c \lt a \lt d \\\ 0 & \text{otherwise} \end{cases} }\)
25 Are there any relationship between delta function and Heaviside function?
25.1 Front
Are there any relationship between delta function and Heaviside function?
What’s the relationship?
25.2 Back
\({\displaystyle \delta(t) = \dd{u}(t)}\)
Because \(u(t)\) has a jump at \(0\), \(\delta(t)\) is not a derivative in the usual sense, but it called a generalized derivative
26 Describe by words what is the delta function \(\delta(t)\)
26.1 Front
Describe by words what is the delta function $\delta(t)$
26.2 Back
It’s defined as a limit of a sequence of box functions, all with unit area and which, in the limit \(h \to 0\), become a infinite spike over \(t = 0\)
You should think of \(\delta(t)\) as any function of unit area, concentrated very near \(t = 0\)
Also, \(\delta(t)\) is not a really function. We call it a generalized function
27 What is the value of this integral?
27.1 Front
What is the value of this integral?
\({\displaystyle \int_{-5}^5 7 e^{t^2} \cos(t) \delta(t) \dd{t}}\)
27.2 Back
\({\displaystyle \int_{-5}^5 7 e^{t^2} \cos(t) \delta(t) \dd{t} = 7}\)
All we had to do was evaluate the integrand at \(t=0\)
28 What is the value of this integral?
28.1 Front
What is the value of this integral?
\({\displaystyle \int_{-5}^5 7 e^{t^2} \cos(t) \delta(t - 2) \dd{t}}\)
28.2 Back
\({\displaystyle \int_{-5}^5 7 e^{t^2} \cos(t) \delta(t - 2) \dd{t} = 7 e^4 \cos(2)}\)
All we had to do was evaluate the integrand at \(t=2\)
29 What is the value of this integral?
29.1 Front
What is the value of this integral?
\({\displaystyle \int_{-5}^1 7 e^{t^2} \cos(t) \delta(t-2) \dd{t}}\)
29.2 Back
\({\displaystyle \int_{-5}^1 7 e^{t^2} \cos(t) \delta(t-2) \dd{t} = 0}\)
Since \(t=2\) is not in the interval of integration, the integrand is 0 on the entire interval
30 What is the value of this integral?
30.1 Front
What is the value of this integral?
\({\displaystyle \int_{0^-}^{\infty} \delta(t) \dd{t}}\)
30.2 Back
\({\displaystyle \int_{0^-}^{\infty} \delta(t) \dd{t} = 1}\)
As \(0\) is in the interval \([0^-, \infty)\)
31 What is the value of this integral?
31.1 Front
What is the value of this integral?
\({\displaystyle \int_{0^+}^{\infty} \delta(t) \dd{t}}\)
31.2 Back
\({\displaystyle \int_{0^+}^{\infty} \delta(t) \dd{t} = 0}\)
As \(0\) is not in the interval \([0^+, \infty)\)
32 What is the value of this integral?
32.1 Front
What is the value of this integral?
\({\displaystyle \int_{0^-}^{0^+} \delta(t) \dd{t}}\)
32.2 Back
\({\displaystyle \int_{0^-}^{0^+} \delta(t) \dd{t} = 1}\)
As \(0\), is in the interval \([0^-, 0^+]\). The total area of the box is concentrated at \(0\)
33 What does really mean that \(\delta(t) = u’(t)\)?
33.1 Front
What does really mean that $\delta(t) = u’(t)$?
33.2 Back
\(u(t)\) has a slope of \(0\) except at \(t=0\) that its slope is \(\infty\)
So, it’s derivative is \({\displaystyle u’(t) = \begin{cases} 0 & \text{if } t \neq 0 \\\ \infty & \text{if } t = 0 \end{cases} }\)
This functions shows a spike at \(t=0\), but this derivative does not exits in the calculus sense because of \(u(t)\) is not defined at \(t=0\). So we call this derivative a generalized derivative
You can look at the anti-derivative of \(\delta(t)\)
\({\displaystyle f(t) = \int_{-\infty}^t \delta(\tau) \dd{\tau}}\)
Using the fundamental theorem of calculus leads us to say that \(f’(t) = \delta(t)\) (Also, this is only in a generalized sense since technically the fundamental theorem of calculus requires the integrand to be continuous)
\({\displaystyle f(t) = \begin{cases} 0 & \text{if } t \lt 0 \\\ 1 & \text{if } t \gt 0 \end{cases} }\)
That is, \(f(t) = u(t)\), so \(u(t)\) is the antiderivative of \(\delta(t)\)
34 Get \(f’(t)\) of this function
34.1 Front
Get $f’(t)$ of this function
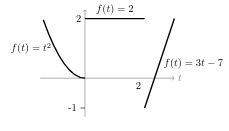
Explain the process to get its derivative. Also draw its graph
34.2 Back
- At smooth parts, it’s derivative is getting as usual
- Each jump discontinuity add a delta scaled by the size of the jump to \(f’(t)\)
\({\displaystyle f’(t) = 2\delta(t) - 3\delta(t-2) + \begin{cases} 2t &\text{if } t \lt 0 \\\ 0 &\text{if } 0 \lt t \lt 2 \\\ 3 &\text{if } 2 \lt t \end{cases} }\)
In the graph for \(f’(t)\) we represent the delta function as spikes with the magnitude written next to the spike. The sign is indicated by the direction of the spike. The rest of the \(f’(t)\) is plotted normally
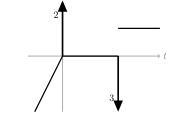
35 What does mean that \(f’(t)\) is a generalized function?
35.1 Front
What does mean that $f’(t)$ is a generalized function?
Explain with words for 18.03 unit
35.2 Back
It’s a sum of a regular function and a linear combination of delta function.
There are 2 parts:
- Singular part
- Delta function pieces
- Regular part
- The remainder of the generalized function
If the singular part contains a multiple of \(\delta(t - a)\) we will say the function contains \(\delta(t - a)\)
36 Describe the parts of this generalized function?
36.1 Front
Describe the parts of this generalized function?
\({\displaystyle f(t) = u(t) + \delta(t) + e^{-t} + 3\delta(t-2)}\)
36.2 Back
- Regular part: \(u(t) + e^{-t}\)
- Singular part: \(\delta(t) + 3\delta(t-2)\)
- The function \(f(t)\) contains \(\delta(t)\) and \(\delta(t-2)\). It does not contain \(\delta(t-1)\)
37 What is the derivative of this expression?
37.1 Front
What is the derivative of this expression?
\(Q(t) = (2t - 2)u(t-1) + u(t-2) + (5 - 2t +1)u(t-3)\)
37.2 Back
\begin{align*} q(t) &= Q’(t) \\\ &= 2u(t-1) + (2 -2)\delta(t-1) + \delta(t-2) + (-2)u(t-3) + (5 - 6 + 1)\delta(t-3)\\\ &= 2(u(t-1) - u(t-3)) + \delta (t-2) \end{align*}