ODE's with Periodic Input, Resonance

Captured On

[2019-11-29 Fri 13:34]

Source

[[https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-iii-fourier-series-and-laplace-transform/odes-with-periodic-input-resonance/index.htm][ODE’s with Periodic Input, Resonance | Unit III: Fourier Series and

Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare]]

1 How can we solve this ODE?

1.1 Front

How can we solve this ODE?

$\ddot{x} + 9.1 x = f(t)$, where $f(t)$ is a odd square wave of period $2\pi$ with $f(t) = 1$ for $0 \lt t \lt \pi$

1.2 Back

• Use the Fourier Series of $f(t)$
  • ${\displaystyle f(t) = \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(nt)}{n}}$
• So the DE: ${\displaystyle \ddot{x} + 9.1 x = \frac{4}{\pi} \biggl(\sin(t) + \frac{\sin(3t)}{3} + \frac{\sin(5t)}{5} + \dots \biggr)}$
• Solve the DE with a single sine function as input
  • ${\displaystyle \ddot{x_n} + 9.1 x_n = \frac{\sin(nt)}{n}}$
  • We use the index $n$ so we can tell our solutions apart
  • Using the superposition to add the factor $\frac{4}{\pi}$ and sum of the others $\sin$
• Using complex replacement and ERF
  • ${\displaystyle x_{n,p}(t) = \frac{\sin(nt)}{n (9.1 - n^2)}}$
• Using superposition to get a particular solution $x_p(t)$
  • ${\displaystyle x_{sp}(t) = \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} x_{n,p}(t) = \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(nt)}{n (9.1 - n^2)}}$

This solution is called the steady periodic solution.

2 What is the Fourier Series for this function?

2.1 Front

What is the Fourier Series for this function?

$f(t)$ is a odd square wave of period $2\pi$ with $f(t) = 1$ for $0 \lt t \lt \pi$

By heart

2.2 Back

${\displaystyle \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(nt)}{n}}$

3 As $\omega_{n}$ gets close to 1,3 or 5 what is the dominant frequency in the ouput?

3.1 Front

As $\omega_{n}$ gets close to 1,3 or 5 what is the dominant frequency in the ouput?As $\omega_{}$

${\displaystyle \ddot{x} + \omega_n^2 x = \omega_n^2 f(t)}$

where $f(t)$ is a odd square wave of period $2\pi$ with $f(t) = 1$ for $0 \lt t \lt \pi$

3.2 Back

With $\omega_n$ near $1$ the output resembles a frequency $1$ sine wave. For $\omega_n$ near $3$ the dominant frequency in the output is $3$, there are three peaks in the oscillation over one cycle of the square wave. Likewise for $\omega_n$ near $5$ the dominant frequency is $5$

${\displaystyle f(t) = \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(nt)}{n}}$

Each term in the series affects the system. If the system has natural frequency $3$ then the $\sin(3t)$ term causes it to resonate with a large amplitude at that frequency. Thus, the response to that term is far larger than the response to any other term.

4 How can we solve this damped harmonic oscillator?

4.1 Front

How can we solve this damped harmonic oscillator?

$\ddot{x} + 2 \dot{x} + 9x = f(t)$

Where $f(t)$ is a triangle wave

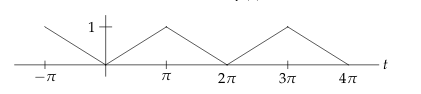
4.2 Back

• Get the Fourier Series of $f(t)$
  • ${\displaystyle f(t) = \frac{1}{2} - \frac{4}{\pi^2} \biggl(\cos(t) + \frac{\cos(3t)}{3^2} + \frac{\cos(5t)}{5^2} + \cdots \biggr)}$
• Solving for the individual components
  • Not including Fourier coefficients of the input in the DE
  • $\ddot{x_n} + 2 \dot{x_n} + 9 x_{n} = \cos(nt)$
  • For $n = 0$, $x_{n,p} = 1/9$
  • For $n \geq 1$
    • Complex replacement: $\ddot{z_n} + 2 \dot{z_n} + 9 z_n = e^{int}$, where $x_n = \operatorname{Re}(z_n)$
    • ERF: ${\displaystyle z_{n,p} = \frac{e^{int}}{9 - n^2 + 2in}}$
    • Polar coordinates: $9 - n^2 + 2in = R_n e^{i \phi_n}$
      • $R_n = \sqrt{(9 - n^2)^2 + 4n^2}$
      • $\phi_n = \operatorname{Arg}(9 - n^2 + 2in) = \arctan \frac{2n}{9 - n^2}$
    • Thus, ${\displaystyle z_{n,p} = \frac{1}{R_n} e^{i(nt - \phi_n)}}$, which implies $x_{n,p} = \frac{\cos(nt - \phi_n)}{R_n}$
• Superposition
  • Adding Fourier coefficients
  • ${\displaystyle x_{sp}(t) = \frac{1}{18} - \frac{4}{\pi^2} \biggl(\frac{\cos(t - \phi_1)}{R_1} + \frac{\cos(3t - \phi_3)}{3^2 R_3} + \frac{\cos(5t - \phi_5)}{5^2 R_5} + \cdots \biggr)}$

5 For which values of $\omega_{n}$ this solution is not periodic?

5.1 Front

For which values of $\omega_{n}$ this solution is not periodic?

${\displaystyle x_p(t) = \frac{\pi}{2 \omega_n^2} - \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\cos(k \omega t)}{k^2(\omega_n^2 - k^2 \omega^2)}}$

For this oscillator: $\ddot{x} + \omega_n^2 x = f(t)$, where ${\displaystyle f(t) = \frac{\pi}{2} - \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\cos(k \omega t)}{k^2}}$

5.2 Back

This solution experiences a resonance if and only if $\omega_n$ (natural frequency of the system) coincides with the angular frequency of a term with nonzero coefficient in the Fourier expansion of the driving function $f(t)$

So, we get periodic solutions for all $\omega_n \neq k(0, 1, 3, 5, 7, \dots) \omega$

6 Are there frequencies at which there is more than one periodic solution?

6.1 Front

Are there frequencies at which there is more than one periodic solution?

For the oscillator system: $\ddot{x} + \omega_n^2 x = f(t)$, where ${\displaystyle f(t) = \frac{\pi}{2} - \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\cos(k \omega t)}{k^2}}$

It’s particular solution is ${\displaystyle x_p(t) = \frac{\pi}{2 \omega_n^2} - \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\cos(k \omega t)}{k^2(\omega_n^2 - k^2 \omega^2)}}$

6.2 Back

Yes, for special frequencies. The homogeneous solution for the system is

${\displaystyle x_h = c_1 \cos(\omega_n t) + c_2 \sin(\omega_n t)}$

If the steady periodic solution, $x_p$, has a period in common with $x_h$ then we can add them together to get many solutions with that common period.

• Base period of $x_h$ is $2\pi / \omega_n$
• Base period of $x_p$ is $2\pi / \omega$ provided $\omega_n \neq 0, \omega, 3 \omega, \dots$

The functions $x_h$ and $x_p$ have a common period when some positive integer multiple of the base period of $x_h$ equals a multiple of the base period of $x_p$

${\displaystyle M \frac{2\pi}{\omega_n} = N \frac{2\pi}{\omega}}$, for some positive integers $M$ and $N$. So

${\displaystyle \omega_n = \frac{M}{N} \omega}$

There is more than one periodic solution if $\omega_n$ is any positive rational multiple of $\omega$ except $1,3,5, \dots$

7 When can we say that this system is in pure resonance without calculating the solution?

7.1 Front

When can we say that this system is in pure resonance without calculating the solution?

$m \ddot{x} + k x = f(t)$, where $f(t)$ is a periodic function

7.2 Back

The natural frequency of the spring-mass system is ${\displaystyle \omega_n = \sqrt{\frac{k}{m}}}$

The typical term of the Fourier expansion of $f(t)$ is ${\displaystyle \cos(n \frac{\pi}{L} t)}$ and ${\displaystyle \sin(n \frac{\pi}{L} t)}$; thus we get pure resonance if and only if the angular frequency of any of the Fourier terms is equals to $\omega_n$,

${\displaystyle \omega_n = \frac{n \pi}{L}}$, where $n$ is an integer

8 How can we expand this expression?

8.1 Front

How can we expand this expression?

${\displaystyle \sum_{n \text{odd}}^{\infty} \sin(n(t + \pi/2))}$

8.2 Back

${\displaystyle \cos(t) - \cos(3t) + \cos(5t) - \cos(7t) + \cdots}$