Operations on Fourier Series

Captured On

[2019-11-23 Sat 18:11]

Source

Operations on Fourier Series | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare

1 What is an even function?

1.1 Front

What is an even function?

Let \(f(t)\) be a function, and write examples

1.2 Back

\(f(t)\) is even if \(f(-t) = f(t)\) for all \(t\)

• \(t^2, t^4, t^6, \dots\), any even power of \(t\)
• \(\cos(at)\)
  • power series for \(\cos(at)\) has only even powers of \(t\)
• A constant function

2 What is the integral of even function on a ‘balanced’ interval?

2.1 Front

What is the integral of even function on a ‘balanced’ interval?

Let \(f(t)\) an even function, and \([-L, L]\) the interval

\({\displaystyle \int_{-L}^L f(t) \dd{t}}\)

2.2 Back

\({\displaystyle 2 \int_0^L f(t) \dd{t}}\)

3 This function is even or odd?

3.1 Front

This function is even or odd?

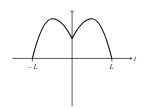
3.2 Back

Even function

4 What is an odd function?

4.1 Front

What is an odd function?

Let \(f(t)\) be a function, and write examples

4.2 Back

\(f(t)\) is odd if \(f(-t) = -f(t)\) for all \(t\)

• \(t, t^3, t^5, \dots\) any odd powers of \(t\)
• \(\sin(at)\)
  • Power series of \(\sin(at)\) has only odd powers of \(t\)

5 What is the integral of odd function on a ‘balanced’ interval?

5.1 Front

What is the integral of odd function on a ‘balanced’ interval?

Let \(f(t)\) be an odd function, and \([-L, L]\) the interval

\({\displaystyle \int_{-L}^L f(t) \dd{t}}\)

5.2 Back

\(0\)

6 How is the outcome function after multiplicate these functions?

6.1 Front

How is the outcome function after multiplicate these functions?

\(\text{even} \cross \text{even}\)

6.2 Back

\(\text{even} \cross \text{even} = \text{even}\)

Thinks in terms of multiply even or odd powers of \(t\)

7 How is the outcome function after multiplicate these functions?

7.1 Front

How is the outcome function after multiplicate these functions?

\(\text{odd} \cross \text{odd}\)

7.2 Back

\(\text{odd} \cross \text{odd} = \text{even}\)

Thinks in terms of multiply even or odd powers of \(t\)

8 How is the outcome function after multiplicate these functions?

8.1 Front

How is the outcome function after multiplicate these functions?

\(\text{odd} \cross \text{even}\)

8.2 Back

\(\text{odd} \cross \text{even} = \text{odd}\)

Thinks in terms of multiply even or odd powers of \(t\)

9 How are the Fourier coefficients when \(f(t)\) is even?

9.1 Front

How are the Fourier coefficients when $f(t)$ is even?

Let \(f(t)\) be an even function

9.2 Back

\(b_n = 0\), multiplying and even and odd function, the integrand is odd, so the integral is \(0\)

\({\displaystyle a_n = \frac{2}{L} \int_0^L f(t) \cos(n \frac{\pi}{L} t) \dd{t}}\)

Multiplying 2 even functions, the integrand is even.

10 How are the Fourier coefficients when \(f(t)\) is odd?

10.1 Front

How are the Fourier coefficients when $f(t)$ is odd?

Let \(f(t)\) be an odd function

10.2 Back

\(a_n = 0\), because of the integrand is odd, so the integral is \(0\)

\({\displaystyle b_n = \frac{2}{L} \int_0^L f(t) \sin(n \frac{\pi}{L} t) \dd{t}}\)

The integrand is even after multiply 2 odd functions

11 Shift vertically this odd function by 1 upwards unit?

11.1 Front

Shift vertically this odd function by 1 upwards unit?

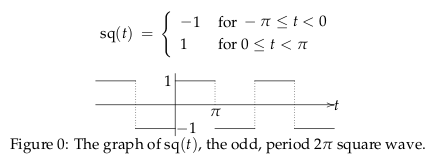
Where \({\displaystyle sq(t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

11.2 Back

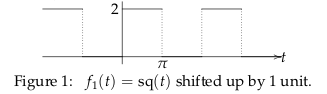
\({\displaystyle f_1 (t) = 1 + sq(t) = 1 + \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

12 Scale vertically this odd function by 2 upwards units?

12.1 Front

Scale vertically this odd function by 2 upwards units?

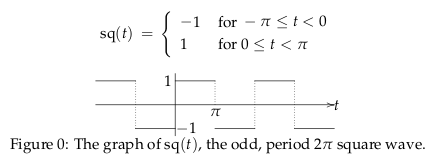
Where \({\displaystyle sq(t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

12.2 Back

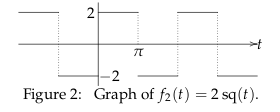
\({\displaystyle f_2(t) = 2 sq(t) = \frac{8}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

13 Shift by \(1\) and scale by \(1/2\) vertically this function

13.1 Front

Shift by $1$ and scale by $1/2$ vertically this function

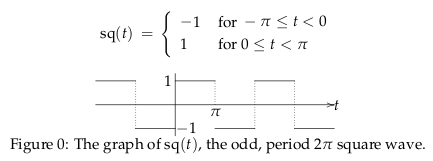
Where \({\displaystyle sq(t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

13.2 Back

\({\displaystyle f_3(t) = \frac{1}{2} \biggl(1 + sq(t) \biggr) = \frac{1}{2} + \frac{2}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

14 Scale in time this function

14.1 Front

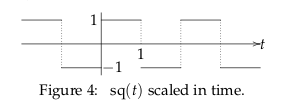
Scale in time this function

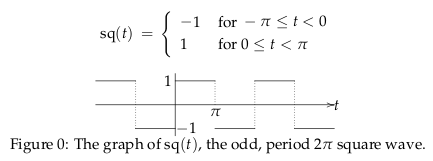
Where \({\displaystyle sq(t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

In the new function \(\pi \to 1\) in time axis

14.2 Back

\({\displaystyle f_4 (t) = sq(\pi t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(\pi n t)}{n}}\)

15 Shift in time by \(\pi/2\) to the left this function

15.1 Front

Shift in time by $\pi/2$ to the left this function

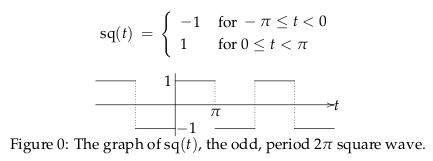
Where \({\displaystyle sq(t) = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

15.2 Back

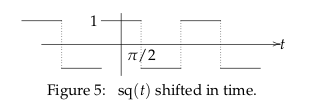
\({\displaystyle f_5(t) = sq(t + \pi/2) = \frac{4}{\pi} \biggl(\sin(t + \pi/2) + \frac{\sin(3t + 3\pi/2)}{3} + \cdots \biggr) = \frac{4}{\pi} \biggl(\cos(t) - \frac{\cos(3t)}{3} + \cdots \biggr)}\)

\(f_5(t)\) is an even function, so you must have only cosine terms in its series

16 How can you integrate a Fourier series

16.1 Front

How can you integrate a Fourier series

Let \(f(t)\) be a Fourier series

Will it be a periodic function?

16.2 Back

Term by terms, but the outcome isn’t a Fourier series (it’s not periodic), because of the \(t\) term

17 How can you differentiate a Fourier Series?

17.1 Front

How can you differentiate a Fourier Series?

Let \(f(t)\) be a Fourier series

17.2 Back

Term by term

18 What is the result of derivative a triangle wave function?

18.1 Front

What is the result of derivative a triangle wave function?

Let \(f(t)\) be the period of \(2\pi\) triangle wave (continuous sawtooth) given on the interval \([-\pi, \pi]\) by \(f(t) = \abs{t}\)

\({\displaystyle f(t) = \frac{\pi}{2} - \frac{4}{\pi} \biggl(\cos(t) + \frac{\cos(3t)}{3^2} + \frac{\cos(5t)}{5^2} + \cdots \biggr)}\)

18.2 Back

The derivative terms by terms of this function, give us a square wave.

\({\displaystyle f’(t) = \frac{4}{\pi} \biggl(\sin(t) + \frac{\sin(3t)}{3} + \frac{\sin(5t)}{5} + \cdots \biggr)}\)

19 What does mean to differentiate a square wave functions?

19.1 Front

What does mean to differentiate a square wave functions?

\({\displaystyle sq(t) = \frac{4}{\pi} \biggl(\sin(t) + \frac{\sin(3t)}{3} + \frac{\sin(5t)}{5} + \cdots \biggr)}\)

19.2 Back

You can differentiate this function term-by-terms, but as \(sq(t)\) consists of horizontal segments its derivative at most places is 0. However we can’t ignore the ‘vertical’ segments where the function has jump discontinuity

You need delta functions and generalized derivatives

20 What is a piecewise smooth function?

20.1 Front

What is a piecewise smooth function?

Let \(f(t)\) be a \(2L\) periodic function

20.2 Back

\(f(t)\) is called piecewise smooth

• if there are a only finite number of points \(0 \leq t_1 \lt t_2 \lt \dots \lt t_n \leq 2L\) where \(f(t)\) is not differentiable, and
• if at each of these points the left and ther righ-hand limits \({\displaystyle \lim_{t \to t_i^-} f’(t)}\) and \({\displaystyle \lim_{t \to t_i^+} f’(t)}\) exist (although they might not be equal)

Example:

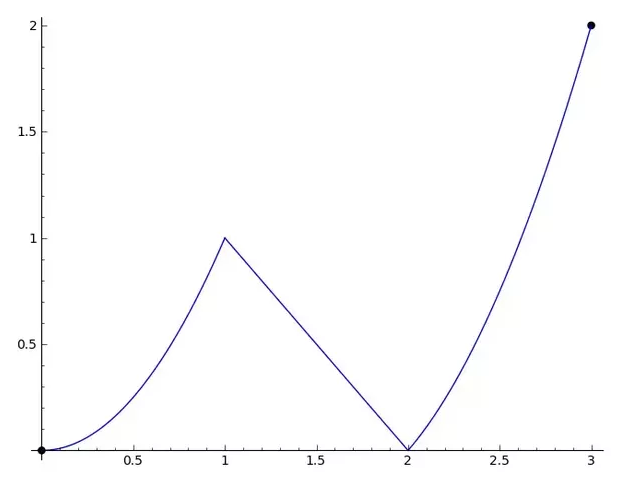
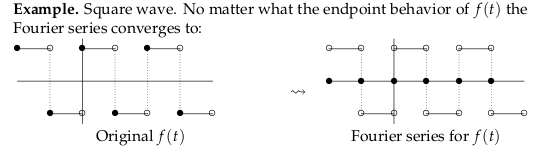
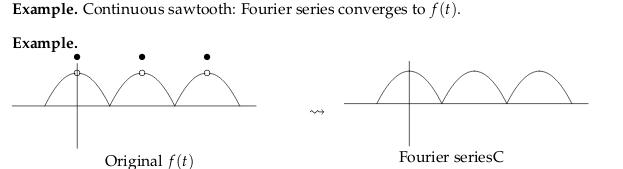
21 Are the functions and its Fourier series exactly the same function?

21.1 Front

Are the functions and its Fourier series exactly the same function?

Put examples

21.2 Back

Not, it’s not, it really quite similar but isn’t the same

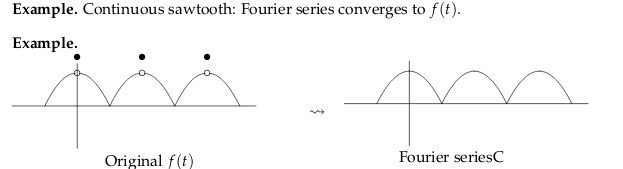
22 How converges a Fouries series of \(f(t)\)

22.1 Front

How converges a Fouries series of $f(t)$

Let \(f(t)\) be the a function

22.2 Back

\(f(t)\) must be a periodic piecewise smooth function, then its Fourier series:

• converges to \(f(t)\) at values of \(t\) where \(f\) is continuous
• converges to the average of \(f(t^-)\) and \(f(t^+)\) where it has a jump discontinuity

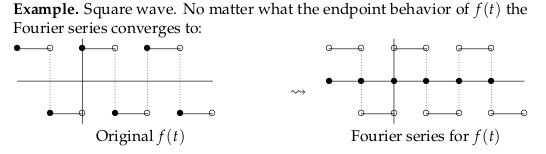
23 What is the Fourier Analysis?

23.1 Front

What is the Fourier Analysis?

23.2 Back

It’s the decomposition of a function \(f(t)\) into the sum of its sinusoidal harmonics, which are also called its Fourier components

For example, the ear is a fourier analyzer

24 What is the Fourier Synthesis?

24.1 Front

What is the Fourier Synthesis?

24.2 Back

It’s the building up of a function \(f(t)\) by adding up its successive Fourier components, that is, the reconstruction of a function \(f(t)\) from its Fourier components.

For example, the brain is a Fourier synthesizer

25 Why there is an overshoot near the discontinity on a Fourier series?

25.1 Front

Why there is an overshoot near the discontinity on a Fourier series?

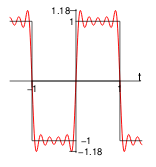
In this picture, the overshoot is about \(0.18\)

25.2 Back

It’s called Gibbs’ phenomenon, and doesn’t matter how many terms are include in the Fourier series. The overshoot always be about \(9%\) of the size of the jump.

In this case, the overshoot is \(0.18\) that it’s the \(9%\) of the jump of \(2\)

26 Given this Fourier Series, what is the value of this formula?

26.1 Front

Given this Fourier Series, what is the value of this formula?

Let \({\displaystyle f(t) = \frac{\pi^2}{3} - 2 \sum_{n=1}^{\infty} \frac{\cos(nt)}{n^2}}\) be the Fouries series of \({\displaystyle f(t) = t \biggl(\pi - \frac{t}{2}\biggr)}\) on \([0, 2\pi]\)

Formula: \({\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2}}\)

26.2 Back

Since the function \(f(t)\) is continuous, the series converges to \(f(t)\) for all \(t\). Pluggin in \(t = 0\), we get

\({\displaystyle f(0) = 0 = \frac{\pi^2}{3} - \sum_{n=1}^{\infty} \frac{2}{n^2}}\)

so, \({\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}}\)

27 What is the Fourier series for this function?

27.1 Front

What is the Fourier series for this function?

\({\displaystyle f(t) = \cos(2t - \frac{\pi}{4})}\)

27.2 Back

This function is a trigonmetric function, which could be decomposing using the trigonometric identity \(\cos(A - B) = \cos(A) \cos(B) + \sin(A) \sin(B)\)

\({\displaystyle f(t) = \cos(2t) \cos(\frac{\pi}{4}) + \sin(2t) \sin(\frac{\pi}{4}) = \frac{1}{\sqrt{2}} \biggl(\cos(2t) + \sin(2t) \biggr)}\)

28 Given this Fourier series compute \(f(t)\) Fourier series?

28.1 Front

Given this Fourier series compute $f(t)$ Fourier series?

\({\displaystyle sq(t) = \begin{cases} -1 & -\pi \lt t \lt 0 \ 1 & 0 \lt t \lt \pi \end{cases} = \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n}}\)

\({\displaystyle f(t) = \abs{t}}\) on \(-\pi \lt t \lt \pi\) with period \(2\pi\)

28.2 Back

We can see that \(f’(t) = sq(t)\) on the interval, so \(f(t) = \int sq(t) \dd{t}\)

\({\displaystyle f(t) = \int \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} \frac{\sin(nt)}{n} \dd{t} = C + \frac{4}{\pi} \sum_{n \text{odd}}^{\infty} - \frac{\cos(nt)}{n^2}}\)

The constant \(C\) could be get using Fourier coefficients

\({\displaystyle C = \frac{1}{2\pi} \int_{-\pi}^{\pi} \abs{t} \dd{t} = \frac{1}{\pi} \int_0^{\pi} t \dd{t} = \frac{1}{\pi} \frac{\pi^2}{2} = \frac{\pi}{2}}\)

29 How could we get a Fourier series from square wave Fouries series?

29.1 Front

How could we get a Fourier series from square wave Fouries series?

Square wave: \(sq(t) = 1\) for \(0 \lt t \lt \pi\), it’s a \(2\pi\) period odd function, which Fourier series is \({\displaystyle \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(nt)}{n}}\)

Find Fourier Series for \(h(t)\) which is a odd and periodic of period \(2\pi\) and such that \(h(t) = t\) for \({\displaystyle 0 \lt t \lt \frac{\pi}{2}}\) and \(h(t) = \pi - t\) for \({\displaystyle \frac{\pi}{2} \lt t \lt \pi}\)

29.2 Back

We can see that \(sq(t)\) could be the derivative of \(h(t)\) but first we need to resize it on time axis from \(\pi\) to \(\pi / 2\)

\begin{align*} h’(x) &= sq(t + \pi/2) \\\ &= \frac{4}{\pi} \sum_{n \text{ odd}}^{\infty} \frac{\sin(n (t + \pi / 2))}{n} \\\ &= 1 + \frac{4}{\pi} \cos(t) - \frac{4}{3 \pi} \cos(3t) + \frac{4}{5\pi} \cos(5t) + \cdots \end{align*}

So, the Fourier Series of \(h(t)\) is

\begin{align*} h(x) &= \int sq(t + \pi / 2) \dd{t} \\\ &= \int 1 + \frac{4}{\pi} \cos(t) - \frac{4}{3 \pi} \cos(3t) + \frac{4}{5\pi} \cos(5t) + \cdots \dd{t} \\\ &= \frac{4}{\pi} \sin(t) - \frac{4}{9\pi} \sin(3t) + \frac{4}{25\pi} \sin(5t) + \cdots \end{align*}

\(h(t)\) doesn’t have constant because it’s a odd function

30 What is the Fourier Series for this function?

30.1 Front

What is the Fourier Series for this function?

\(\sin^2(t)\)

30.2 Back

Using trigonometric identity of double angle formula \(\cos(2t) = 1 - 2 \sin^2(t)\)

\({\displaystyle \sin^2(t) = \frac{1}{2} - \frac{1}{2} \cos(2t)}\)

• As \(\sin^2(t)\) it’s an even function, there is no \(b_n\) coefficients
• This function has a base period of \(\pi\)

31 Why any function \(F(x)\) is a sum of an even function an an odd function?

31.1 Front

Why any function $F(x)$ is a sum of an even function an an odd function?

So, that the decomposition is unique

31.2 Back

• Even function from \(F(x)\): \(F(x) + F(-x)\)
  • \(h(x) = f(x) + f(-x)\)
  • \(h(-x) = f(-x) + f(x)\)
  • \(h(x) = h(-x)\), that is an even function
• Odd function from \(F(x)\): \(F(x) - F(-x)\)
  • \(h(x) = f(x) - f(-x)\)
  • \(h(-x) = f(-x) - f(-x)\)
  • \(-h(x) = h(-x)\), that is an odd function

Adding both functions: \(F(x) + F(-x) + F(x) - F(-x) = 2 F(x)\), so

\({\displaystyle F(x) = \frac{F(x) + F(-x)}{2} + \frac{F(x) - F(-x)}{2}}\)

To show that this decomposition is unique, we suppose we have another decomposition \({\displaystyle F_{\text{even}}(x) + F_{\text{odd}}(x) = F(x) = \frac{F(x) + F(-x)}{2} + \frac{F(x) - F(-x)}{2}}\)

Rearranging terms, this means that

\({\displaystyle f_{\text{even}}(t) - \frac{F(x) + F(-x)}{2} = -F_{\text{odd}}(x) + \frac{F(x) - F(-x)}{2}}\)

This sum of the LHS must be even, and the sum of the RHS must be odd. But then each side is simultaneously both even and odd, and has to be zero.

Thus: \({\displaystyle F_{\text{even}} = \frac{F(x) + F(-x)}{2}}\) and \({\displaystyle F_{\text{odd}} = \frac{F(x) - F(-x)}{2}}\)

32 What is the even part of \(e^{x}?\)

32.1 Front

What is the even part of $e^{x}$?

32.2 Back

\({\displaystyle \frac{e^x + e^{-x}}{2} = \cosh x}\)

33 What is the odd part of \(e^{x}\)?

33.1 Front

What is the odd part of $e^{x}$?

33.2 Back

\({\displaystyle \frac{e^x - e^{-x}}{2} = \sinh x}\)

34 Compute the Fourier Series for this function?

34.1 Front

Compute the Fourier Series for this function?

\(2 \sin(t - \frac{\pi}{3})\)

34.2 Back

\({\displaystyle 2 \sin(t - \frac{\pi}{3}) = 2 \biggl( \cos(\frac{\pi}{3})\sin(t) - \sin(\frac{\pi}{3}) \cos(t) \biggr) = \sin(t) - \sqrt{3} \cos(t)}\)

35 Is this relationship equals?

35.1 Front

Is this relationship equals?

\(\sin(2\pi t) = \sin(t)\)

35.2 Back

Not, it isn’t the same