- Captured On
- Source
- Fourier Series: Basics | Unit III: Fourier Series and Laplace Transform | Differential Equations | Mathematics | MIT OpenCourseWare
1 Which is the minimum period of a constant function?
1.1 Front
Which is the minimum period of a constant function?
1.2 Back
There is no minimal period, we don’t allow \(P = 0\) to be periodic.
Also, for any \(P\) value is a period, but no minimal
2 What is a base period of a periodic function?
2.1 Front
What is a base period of a periodic function?
2.2 Back
It’s the minimal value period \(P\) for \(f(t + P) = f(t)\) for all \(t\)
3 What the period \(P\) for this function?
3.1 Front
What the period $P$ for this function?
\(f(t) = \sin(2t)\), and its base period
3.2 Back
It has period \(P = n\pi\) for any integer \(n = 1,2,3, \dots\). The base period is \(\pi\)
4 What is a periodic function?
4.1 Front
What is a periodic function?
4.2 Back
Are functions which repeat \(f(t + P) = f(t)\) for all \(t\), where \(P \gt 0\)
5 What are the typical definition of a window in periodic function?
5.1 Front
What are the typical definition of a window in periodic function?
5.2 Back
It’s the interval for fully description of a periodic function. It’s contains a full period of this function.
- \([ - P/2, P/2)\)
- \([0, P)\)
- Any other interval of length \(P\)
6 What is the difference between frequency and angular frequency?
6.1 Front
What is the difference between frequency and angular frequency?
What is the relationship between these 2 concepts?
6.2 Back
Angular frequency has units of radians/unit time and frequency has units of cycles/unit time. Where one cycle has \(2 \pi\) radians.
\(\text{angular frequency } = 2\pi \cross \text{ frequency} = \frac{2\pi}{P}\)
Angular frequency is also called circular frequency
7 What is a Fourier Series?
7.1 Front
What is a Fourier Series?
Explain with words
7.2 Back
A periodic function with base frequency \(\omega\) can be written as a sum of sines and cosines whose frequencies are integer multiples of \(\omega\). This is called the Fourier Series for the function.
8 Which collection of cosine functions all have \(2\pi\) period?
8.1 Front
Which collection of cosine functions all have $2\pi$ period?
8.2 Back
For \(n=1,2,3, \dots, \cos(nt)\) has period \(2\pi\), and base period \(2\pi / n\)
9 Which collection of sine functions all have \(2 \pi\) period?
9.1 Front
Which collection of sine functions all have $2 \pi$ period?
9.2 Back
For \(n=1,2,3, \dots, \sin(nt)\) has period \(2\pi\), and base period \(2\pi / n\)
10 What is the base (fundamental) frequency of the function?
10.1 Front
What is the base (fundamental) frequency of the function?
\(f(t) = \cos(t) + \cos(2t) + \cos(3t)\)
10.2 Back
The smallest common period of \(\cos(t)\), \(\cos(2t)\) and \(\cos(3t)\) is \(2\pi\). Thus, \(f(t)\) has minimal period \(P = 2\pi\), and therefore its base frequency \(\omega\) is \(\frac{2\pi}{P} = 1\)
11 What is the Fourier theorem for periodic functions?
11.1 Front
What is the Fourier theorem for periodic functions?
Suppose \(f(t)\) has period \(2 \pi\)
11.2 Back
\({\displaystyle f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nt) + b_n \sin(nt)}\)
where the Fourier coefficients* are computed by:
- \({\displaystyle a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) dt}\)
- \({\displaystyle a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos(nt) dt}\)
- \({\displaystyle b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \sin(nt) dt}\)
the RHS is called Fourier series
12 Why we don’t need to calculate \(b_{0}\) in the Fourier theorem?
12.1 Front
Why we don’t need to calculate $b_{0}$ in the Fourier theorem?
Suppose \(f(t)\) has period \(2 \pi\)
12.2 Back
Because \(\sin(0 \cdot t) = 0\)
13 Write the exponential equivalent for this expression
13.1 Front
Write the exponential equivalent for this expression
\(cos(n \pi)\)
13.2 Back
\((-1)^n\)
14 Expand the Fourier series with this coefficients
14.1 Front
Expand the Fourier series with this coefficients
- \(a_0 = 0\)
- \(a_n = 0\)
- \(b_n = \frac{4}{\pi n}\) if \(n\) is odd
- \(b_n = 0\) if \(n\) is even
14.2 Back
\({\displaystyle f(t) = \sum_{n=1}^{\infty} b_n \sin(nt) = \frac{4}{\pi} \biggl( \sin(t) + \frac{1}{3} \sin(3t) + \frac{1}{5} \sin(5t) + \cdots \biggr)}\)
15 How is the Fourier Series of a odd function?
15.1 Front
How is the Fourier Series of a odd function?
15.2 Back
Odd function: \(f(-t) = -f(t)\)
This kind of function only have sines (which is also odd functions) in their Fourier series
\({\displaystyle f(t) = \sum_{n=1}^{\infty} b_n \sin(nt)}\)
16 How is the Fourier series for even functions?
16.1 Front
How is the Fourier series for even functions?
16.2 Back
Even function: \(f(-t) = f(t)\)
This kind of function only have cosine (which is also even function) in their Fourier series
\({\displaystyle f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nt)}\)
17 How is the graph of the Fourier Series of this function?
17.1 Front
How is the graph of the Fourier Series of this function?

\(f(t) = \frac{4}{\pi} \biggl( \sin(t) + \frac{1}{3} \sin(3t) + \frac{1}{5} \sin(5t) + \cdots \biggr)\)
17.2 Back
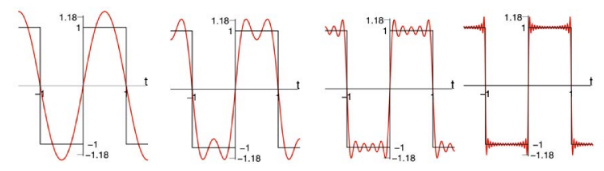
18 Which is the Fourier Series for function with Period 2L?
18.1 Front
Which is the Fourier Series for function with Period 2L?
\(f(t)\) with period \(P = 2L\)
18.2 Back
\({\displaystyle f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(n \frac{\pi}{L}t) + b_n \sin(n \frac{\pi}{L} t)}\)
with Fourier coefficients given by the general Fourier coefficients formula
- \({\displaystyle a_0 = \frac{1}{L} \int_{-L}^L f(t) \dd{t}}\)
- \({\displaystyle a_n = \frac{1}{L} \int_{-L}^L f(t) \cos(n \frac{\pi}{L} t) \dd{t}}\)
- \({\displaystyle b_n = \frac{1}{L} \int_{-L}^L f(t) \sin(n \frac{\pi}{L} t) \dd{t}}\)
Where \(L = \frac{P}{2}\) is called the half-period
19 How is the graph of this function?
19.1 Front
How is the graph of this function?
Let \(f(t)\) be the period 2 function, which is defined on the window \([-1, 1)\) by \(f(t) = \abs{t}\)
19.2 Back
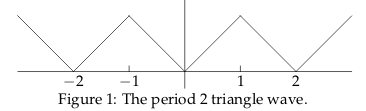
20 Which is the principle of orthogonality for 2 periodic functions?
20.1 Front
Which is the principle of orthogonality for 2 periodic functions?
Let \(u(t)\) and \(v(t)\) 2 distinct functions on \(\mathbb{R}\) with \(P = 2L\)
20.2 Back
These 2 functions are orthogonal if
\({\displaystyle \int_{-L}^L u(t) v(t) \dd{t} = 0}\)
21 Are any of 2 function of this collection orthogonal?
21.1 Front
Are any of 2 function of this collection orthogonal?
Collection:
- \(\sin(nt)\) for \(n=1, \dots, \infty\)
- \(\cos(mt)\) for \(m=0, \dots, \infty\)
21.2 Back
Only if these 2 function are distinct, I mean \(\sin\) and \(\cos\) are orthogonal on \([-\pi, \pi]\).
Otherwise, this value of \({\displaystyle \int_{-\pi}^{\pi} \cos^2(nt) \dd{t}}\) or \({\displaystyle \int_{-\pi}^{\pi} \sin^2(nt) \dd{t}}\) is always positive
22 Are the value of these integrals different?
22.1 Front
Are the value of these integrals different?
\({\displaystyle \int_{-\pi}^{\pi} \sin^2(nt) \dd{t} \neq \int_{-\pi}^{\pi} \cos^2(nt) \dd{t}}\)
What are its values?
22.2 Back
No, it has the same value, it’s \(\pi\)
23 What is the ODE which satisfies any of these functions?
23.1 Front
What is the ODE which satisfies any of these functions?
- \(\sin(nt)\)
- \(\cos(nt)\)
23.2 Back
\(u_n’’ + n^2 u_n = 0\)
24 What could be a solution of this ODE?
24.1 Front
What could be a solution of this ODE?
\(u’’ + n^2 u = 0\), where \(u = u(t)\)
24.2 Back
- \(\sin(nt)\)
- \(\cos(nt)\)
25 What is the value of this integral?
25.1 Front
What is the value of this integral?
\({\displaystyle \int_{-L}^L \cos(n \frac{\pi}{L} t) \cos(m \frac{\pi}{L} t) \dd{t}}\)
25.2 Back
Depends on \(n\) and \(m\)
- \(n = m \neq 0 \implies L\)
- \(n \neq m \implies 0\)
- \(n = m = 0 \implies 2L\)
26 What is the value of this integral?
26.1 Front
What is the value of this integral?
\({\displaystyle \int_{-L}^L \sin(n \frac{\pi}{L} t) \sin(m \frac{\pi}{L} t) \dd{t}}\)
26.2 Back
Depends on the values of \(n\) and \(m\)
- \(n = m \neq 0 \implies L\)
- \(n \neq m \implies 0\)
- \(n = m = 0 \implies 0\)
27 What is the value of this integral?
27.1 Front
What is the value of this integral?
\({\displaystyle \int_{-L}^L \cos(n \frac{\pi}{L} t) \sin(m \frac{\pi}{L} t) \dd{t}}\)
27.2 Back
Always is 0, because of these functions are orthogonal on \([-L, L]\)
28 Which methods could we use for proof orthogonality relation?
28.1 Front
Which methods could we use for proof orthogonality relation?
\({\displaystyle \int_{-\pi}^{\pi} \sin(nt) \cos(mt) \dd{t} = 0}\)
28.2 Back
- Trig identities
- \({\displaystyle \cos(\alpha) \cos(\beta) = \frac{1}{2} \biggl(\cos(\alpha + \beta) + \cos(\alpha - \beta) \biggr)}\)
- \({\displaystyle \cos(\alpha) \sin(\beta) = \frac{1}{2} \biggl(\sin(\alpha + \beta) - \sin(\alpha - \beta) \biggr)}\)
- \({\displaystyle \sin(\alpha) + \sin(\beta) = \frac{1}{2} \biggl(\cos(\alpha - \beta) - \cos(\alpha + \beta) \biggr)}\)
- Use complex relation
- \({\displaystyle \cos(at) = \frac{1}{2} \biggl(e^{iat} + e^{-iat} \biggr)}\)
- \({\displaystyle \sin(at) = \frac{1}{2i} \biggl(e^{iat} - e^{-iat} \biggr)}\)
- Using the ODE for trigonometric function \(\sin\) and \(\cos\)
- \(u’’ + n^2 u = 0\)
29 How can we get the Fourier coefficients value?
29.1 Front
How can we get the Fourier coefficients value?
Let \(f(t)\) be a periodic function with period \(P = 2L\) which Fourier series is
\({\displaystyle f(t) = a_0 + \sum_{n=1}^{\infty} a_n \cos(n \frac{\pi}{L} t) + b_n \sin(n \frac{\pi}{L} t)}\)
29.2 Back
- Suppose that we expand the sums
- \({\displaystyle f(t) = a_0 + \cdots + a_k \cos(k \frac{\pi}{L} t) + \cdots + a_n \cos(n \frac{\pi}{L} t) + \cdots}\)
- Multiply both side by \(\cos(n \frac{\pi}{L}t)\)
- \({\displaystyle f(t) \cos(n \frac{\pi}{L}t) = a_0 \cos(n \frac{\pi}{L}t) + \cdots + a_k \cos(k \frac{\pi}{L} t)\cos(n \frac{\pi}{L}t) + \cdots + a_n \cos^2(n \frac{\pi}{L} t) + \cdots}\)
- Integrate both side from \(-L\) to \(L\)
- \({\displaystyle \int_{-L}^L f(t) \cos(n \frac{\pi}{L}t) \dd{t} = \int_{-L}^L \cdots \dd{t}}\)
- Where we get 0 at:
- \({\displaystyle \int_{-L}^L a_0 \cos(n \frac{\pi}{L}t) \dd{t} = 0}\)
- \({\displaystyle \int_{-L}^L a_k \cos(k \frac{\pi}{L} t) \cos(n \frac{\pi}{L}t) \dd{t} = 0}\)
- \({\displaystyle \int_{-L}^L b_k \sin(k \frac{\pi}{L} t) \cos(n \frac{\pi}{L}t) \dd{t} = 0}\)
- But, for \({\displaystyle \int_{-L}^L a_n \cos^2(n \frac{\pi}{L}t) \dd{t} = a_n L}\)
- So, algebraically we get:
- \({\displaystyle a_n = \frac{1}{L} f(t) \cos(n \frac{\pi}{L}t) \dd{t}}\)
We have an special case for \(a_0\), because of \({\displaystyle \int_{-L}^L f(t) \cos(0) \dd{t} = a_0 \int_{-L}^L \dd{t} = a_0 2L}\), so \({\displaystyle a_0 = \frac{1}{2L} \int_{-L}^L f(t) \dd{t}}\)
30 There is any solution of this ODE periodic?
30.1 Front
There is any solution of this ODE periodic?
\(\ddot{x} + \omega_n^2 x = \cos(\omega_n t)\)
30.2 Back
Every homogeneous component here is a periodic function with period \(2\pi / \omega\), but the particular solution we found
\({\displaystyle x_p(t) = \frac{t \sin(\omega_n t)}{2 \omega_n}}\)
is not periodic because there is no periodic \(P\) such that \(f(t + P) = f(t)\) for all \(t\)
So the general solution \(x(t) = x_p(t) + C_1 \cos(\omega_n t) + c_2 \sin(\omega_n t)\)
Note: \(\omega_n \neq 0\), but also is a situation of resonance, \(\ddot{x} = 0\), which solution is \(x = c_1 t + c_2\), that is not periodic (non constant) solution (no oscillating)
31 What is the period of this function?
31.1 Front
What is the period of this function?
\(\abs{\sin(t)}\)
31.2 Back
\(P = \pi\), \(\abs{\sin(t + \pi)} = \abs{- \sin(t)} = \abs{\sin(t)}\)
32 What is the period of this function?
32.1 Front
What is the period of this function?
\(\cos^2(3t)\)
32.2 Back
\({\displaystyle P = \frac{1}{2} \frac{2 \pi}{3} = \frac{\pi}{3}}\)
\({\displaystyle (\cos(3(t + \frac{\pi}{3})))^2 = (\cos(3t + \pi))^2 = (- \cos(3t))^2 = (\cos(3t))^2}\)
33 What is the value of this coefficient?
33.1 Front
What is the value of this coefficient?
\({\displaystyle a_n = \frac{1}{n} \sin(\frac{\pi}{2} n)}\), for \(n\) integer
33.2 Back
- \(n\) even \(a_n = 0\)
- \(n\) odd \(a_n = \frac{1}{n} \sin(\frac{\pi}{2} n)\)
- if \(n = 4a + 1 \implies a_n = \frac{1}{n}\)
- if \(n = 4a + 3 \implies a_n = - \frac{1}{n}\)
34 How could we solve this integral?
34.1 Front
How could we solve this integral?
\({\displaystyle \frac{1}{\pi} \int_{-\pi}^{\pi} \abs{t} \cos(nt) \dd{t}}\)
Don’t solve it if you don’t want
34.2 Back
- Using symmetry, this integral is \({\displaystyle \frac{2}{\pi} \int_{0}^{\pi} t \cos(nt) \dd{t}}\)
- Integrating by parts
- \({\displaystyle \frac{2}{\pi n^2} ( (-1)^n - 1)}\)