Frequency Response and Practical Resonance

Captured On

[2019-11-11 Mon 12:39]

Source

Frequency Response and Practical Resonance | Unit II: Second Order Constant Coefficient Linear Equations | Differential Equations | Mathematics | MIT OpenCourseWare

1 What is the amplitude response of the system?

1.1 Front

What is the amplitude response of the system?

1.2 Back

It’s called to the gain of the system in terms of input angular frequency

2 What is the phase response of the system?

2.1 Front

What is the phase response of the system?

2.2 Back

It’s called to the phase lag function of the system in terms of input angular frequency.

3 What is the frequency response of the system?

3.1 Front

What is the frequency response of the system?

3.2 Back

It’s the amplitude response and phase response of a system. These functions are expressed in terms of input angular frequency.

4 What happens to the frequency response if the input is scaled by $B$?

4.1 Front

What happens to the frequency response if the input is scaled by $B$?

4.2 Back

The amplitude response is scales too by $B$

5 Is the gain always equals to …?

5.1 Front

Is the gain always equals to …?

$\frac{1}{p(i\omega)}$

5.2 Back

No, is the ratio between amplitude of the periodic output and amplitude of the periodic input.

6 What is the practical resonance frequency?

6.1 Front

What is the practical resonance frequency?

6.2 Back

It’s an input frequency $w_r$ where the gain has a peak. It’s depends on the DE, and there are some systems where there is no practical resonance frequency.

In systems like $nx’’ + bx’ + kx = B \cos(\omega t)$, if $b$ is large enough, there no practical resonance

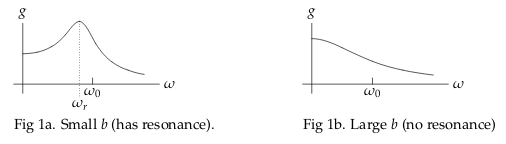
7 How can we find the practical resonant frequency?

7.1 Front

How can we find the practical resonant frequency?

7.2 Back

If practical resonance occurs at frequency $w_r$ is when gain response has a maximum for some $w_r$, so the $g’(w) = 0$ and it’s a maximum.

If the gain is $g(w) = \frac{1}{f(w)}$, then the practical resonant frequency is when $f(w)$ has a minimum.

8 What happens to the phase lag on a damped system?

8.1 Front

What happens to the phase lag on a damped system?

8.2 Back

The damping causes a lag between when the input reaches its maximum and when the output does. In this picture below the dotted line is the input and the solid line is the response. The time lag is ratio $\phi/\omega$

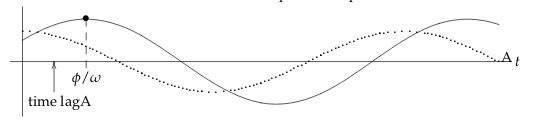
9 Write the DE of this mechanical vibration system?

9.1 Front

Write the DE of this mechanical vibration system?

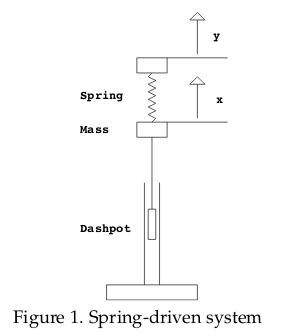
9.2 Back

• $y$ is the displacement of the plunger at the top of the spring
• $x$ is the position of the mass, arranged so that $x=y$ when the spring is unstretched and uncompressed.
• There are 2 forces acting on the mass
  • $F_{\text{spr}} = -k (x - y) = k(y - x)$
  • $F_{\text{dash}} = -b \dot{x}$
• $m \ddot{x} = k(y-x) - b \dot{x}$

Standard form = $m \ddot{x} + b \dot{x} + kx = ky$, where $q = ky$ is the input function and $y$ could be sinusoidal $y = B_1 \cos(\omega t)$.

10 How is the steady state system of this DE?

10.1 Front

How is the steady state system of this DE?

$m \ddot{x} + b \dot{x} + kx = ky$, where $y = B_1 \cos(\omega t)$

10.2 Back

As the input is a sinusoidal function, we expect a sinusoidal particular solution with a form $x_p(t) = A \cos(\omega t - \phi)$, where $A = A(w)$ and $\phi = \phi(w)$ both functions in terms of $\omega$

11 What is the frequency response for this system?

11.1 Front

What is the frequency response for this system?

$m \ddot{x} + b \dot{x} + kx = ky$, where $y = B_1 \cos(\omega t)$ is the input

11.2 Back

As the input signal is sinusoidal, when expect a sinusoidal particular solution, $x_p(t) = A \cos(\omega t - \phi)$

\({\displaystyle g(w) = \frac{A}{B_1} = \frac{k}{\abs{p(i \omega)}} = \frac{k}{\sqrt{(k - m \omega^2)^2 + b^2 \omega^2}}}\)

${\displaystyle \phi(\omega) = \arctan \biggl( \frac{b \omega}{k - m\omega^2} \biggr)}$

12 What is the practical resonant frequency for this system?

12.1 Front

What is the practical resonant frequency for this system?

$m \ddot{x} + b \dot{x} + kx = ky$, where $y = B_1 \cos(\omega t)$

12.2 Back

${\displaystyle \omega_r = \sqrt{\frac{k}{m} - \frac{b^2}{2m^2}}}$

13 Write the DE of this mechanical vibration system?

13.1 Front

Write the DE of this mechanical vibration system?

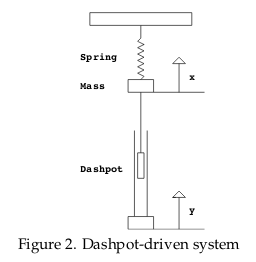
13.2 Back

• Position of the bottom $y(t)$
• Position of the mass is given by $x(t)$, arranged so that $x=0$ when the spring is relaxed

\(m \ddot{x} = -kx + b \dv{t}(y - x)\)

$m \ddot{x} + b \dot{x} + kx = b \dot{y}$

14 How could we get a particular solution for this DE?

14.1 Front

How could we get a particular solution for this DE?

$m \ddot{x} + b \dot{x} + kx = b \dot{y}$, where $y = y(t) = B \cos(\omega t)$

14.2 Back

• Complexify before taking the derivative of the RHS
  • $m \ddot{z} + b \dot{z} + k z = b \widetilde{y}’ = b i \omega B e^{i \omega t}$
  • Since $y = \operatorname{Re}(\widetilde{y})$ and $x = \operatorname{Re}(z)$
• ERF: ${\displaystyle z_p(t) = \frac{i \omega b B}{p(i\omega)} e^{i \omega t}}$
  • where $p(s) = m s^2 + b s + k$ is the characteristic polynomial

15 What is the gain of this DE?

15.1 Front

What is the gain of this DE?

$m \ddot{x} + b \dot{x} + kx = b \dot{y}$, where $y = y(t) = B \cos(\omega t)$ is the input, and its complex solution is ${\displaystyle z_p(t) = \frac{i \omega b B}{p(i\omega)} e^{i \omega t}}$

15.2 Back

${\displaystyle \widetilde{g}(\omega) = \frac{i \omega b}{p(i \omega)}}$, thus ${\displaystyle z_p(t) = B \widetilde{g}(\omega) e^{i \omega t}}$

16 What is the real solution for this DE?

16.1 Front

What is the real solution for this DE?

$m \ddot{x} + b \dot{x} + kx = b \dot{y}$, where $y = y(t) = B \cos(\omega t)$ is the input signal, and ${\displaystyle z_p(t) = \frac{i \omega b B}{p(i\omega)} e^{i \omega t}}$ is the complex solution

16.2 Back

Real solution will have this form: $x_p(t) = A \cos(\omega t - \phi)$, so $g = \frac{A}{B}$

${\displaystyle \widetilde{g}(\omega) = \frac{i \omega b}{p(i \omega)}}$, thus ${\displaystyle z_p(t) = B \widetilde{g}(\omega) e^{i \omega t}}$

We can write \(\widetilde{g}(\omega) = \abs{\widetilde{g}} e^{-i \phi}\), where $\phi = - \operatorname{Arg}(\widetilde{g})$, so \(z_p(t) = B \abs{\widetilde{g}} e^{i(\omega t - \phi)}\)

So, the real solution is \(x_p(t) = B \abs{\widetilde{g}} \cos(\omega t - \phi)\)

• \({\displaystyle g(\omega) = \abs{\widetilde{g}} = \frac{\omega b}{\abs{p(i\omega)}} = \frac{\omega b}{\sqrt{(k - m \omega^2)^2 + b^2 \omega^2}}}\)
• ${\displaystyle \phi(\omega) = - \operatorname{Arg}(\widetilde{g}) = \arctan (- (k - m\omega^2) / (b \omega))}$

17 What is the practical resonant frequency for this DE?

17.1 Front

What is the practical resonant frequency for this DE?

$m \ddot{x} + b \dot{x} + kx = b \dot{y}$, where $y = y(t) = B \cos(\omega t)$ where ${\displaystyle z_p(t) = \frac{i \omega b B}{p(i\omega)} e^{i \omega t}}$

Tip: ${\displaystyle \widetilde{g}(\omega) = \frac{i \omega b}{p(i \omega)}}$

17.2 Back

Divide the numerator and denominator in $\widetilde{g}$ by $bi \omega$

${\displaystyle \widetilde{g} = \frac{1}{1 + (k - m\omega^2)/(i\omega b)} = \frac{1}{1 - i (k -m \omega^2)/(\omega b)}}$

\({\displaystyle g = \abs{\widetilde{g}} = \frac{1}{\sqrt{1 + (k - m\omega^2)^2 / (\omega b)^2}}}\)

The practical resonant frequency occurs when $g$ get its maximum, so $g$ is largest when $k - m\omega^2 = 0$. At this point, $g = 1$ and $\omega_r = \sqrt{k/m} = \omega_0$. Thus, the resonant frequency is the natural frequency

Since $\widetilde{\omega_0} = 1$, the phase lag $\phi = \operatorname{Arg}(\widetilde{g}) = 0$ at $\omega_r$

18 Find a solution of this DE?

18.1 Front

Find a solution of this DE?

$\ddot{x} + 3 \dot{x} + 2x = t e^{-t}$

18.2 Back

Using the method of variation of parameters

Suppose there is a solution of the form $x(t) = u(t)e^{-t}$ for some function $u(t)$. Then $\dot{x} = \dot{u} e^{-t} - u e^{-t}$ and $\ddot{x} = \ddot{u}e^{-t} - 2 \dot{u}e^{-t} + ue^{-t}$

Substituting in the DE:

${\displaystyle \ddot{u} e^{-t} - 2 \dot{u} e^{-t} + u e^{-t} + 3 \dot{u}e^{-t} - 3 u e^{-t} + 2 u e^{-t} = (\ddot{u} + \dot{u})e^{-t} = t e^{-t}}$

The exponential is never zero, so can cancel $e^{-t}$ from both sides and obtain $\ddot{u} + \dot{u} = t$

To solve $u$, we use the method of undetermined coefficients, where the corresponding characteristic polynomial $p(s) = s^2 + s$ has zero constant term and nonzero linear term. So we guess a quadratic polynomial solution $u = at^2 + bt + c$. Plugging this in to the equation, and solving coefficients gives us that ${\displaystyle u = \frac{t^2}{2} - t}$

On solution of the DE is ${\displaystyle x(t) = \biggl( \frac{t^2}{2} - t \biggr) e^{-t}}$

19 How can we know that a system has practical resonant frequency?

19.1 Front

How can we know that a system has practical resonant frequency?

Tip: ${\displaystyle w_r = \sqrt{\frac{k}{m} - \frac{c^2}{2m^2}}}$

19.2 Back

The frequency which gives practical resonance if $c \lt \sqrt{2km}$

20 Rewrite this expression?

20.1 Front

Rewrite this expression?

$\frac{z}{i}$

20.2 Back

$-iz$

21 How can we rotate $-\pi / 2$ a complex number?

21.1 Front

How can we rotate $-\pi / 2$ a complex number?

$z$ complex number

21.2 Back

$z/i$

22 Complete this graph

22.1 Front

Complete this graph

And describe what it is its phase difference

22.2 Back

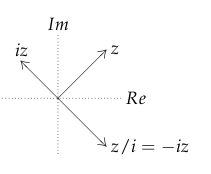
• $z$ and $iz$ have a phase difference of $\pi/2$
• $z$ and $z/i$ have a phase difference of $- \pi / 2$