1 What is the name of this symbol \(p(D)\)?
1.1 Front
What is the name of this symbol $p(D)$?
Where \(D\) is a differential operator
1.2 Back
\(p(D)\) is a polynomial operator
2 What is a polynomial differential operator with constant coefficients?
2.1 Front
What is a polynomial differential operator with constant coefficients?
2.2 Back
\(p(D)\) that you can apply to any function (sufficiently differentible)
\(p(D) = a_0 D^n + a_1 D^{n-1} + \dots + a_n\)
3 What is the sum rule for differential operator \(D\)?
3.1 Front
What is the sum rule for differential operator $D$?
3.2 Back
Suppose that functions involved are sufficiently differentiable
Where \(p(D)\) and \(q(D)\) are polynomial operators
\([p(D) + q(D)]u = p(D)u + q(D)u\)
4 What is the general linear ODE of order \(n\) written with operators?
4.1 Front
What is the general linear ODE of order $n$ written with operators?
4.2 Back
It must have constant coefficients.
\(y^{(n)} + a_1 y^{(n-1)} + \dots + a_n y = q(t)\)
where \(p(D)\) is a polynomial differential operator with constant coefficients, \(p(D) = D^n + a_1 D^{n-1} + \dots + a_n\)
\(p(D) y = q(t)\)
5 What is the linearity rule for differential operator?
5.1 Front
What is the linearity rule for differential operator?
5.2 Back
If \(f\) and \(g\) are functions and \(c_1\) and \(c_2\) are constants,
\({\displaystyle p(D)(c_1 f + c_2 g) = c_1 p(D)f + c_2 p(D)g}\)
6 Can we apply the linearity rule of differential operator of any order?
6.1 Front
Can we apply the linearity rule of differential operator of any order?
\(D^n(c_1 f + c_2 g)\)
6.2 Back
Yes, \({\displaystyle D^n(c_1 f + c_2 g) = c_1 D^n f + c_2 D^n g}\)
7 What does mean this equation?
7.1 Front
What does mean this equation?
If \(f\) and \(g\) are functions and \(c_1\) and \(c_2\) are constants,
\(aD^n(c_1 f + c_2 g)\), \(a\) could be a constant or a function of \(t\)
7.2 Back
\(a \dv[n]{t} (c_1 f + c_2 g) = c_1 a f^{(n)} + c_2 a g^{(n)} = c_1 a D^n f + c_2 a D^n g\)
8 What does means this expression?
8.1 Front
What does means this expression?
\(p(D)u\), where \(p(D) = g(D)h(D)\)
8.2 Back
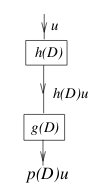
\(D^m(a D^k u) = a D^{m+k} u\), which could be extends to general polynomial operators \(h(D)\) by linearity.
In this case \(a\) must be a constant
9 Is this expression correct?
9.1 Front
Is this expression correct?
\(g(D)(h(D) u) = h(D)(g(D) u)\)
9.2 Back
It’s true if \(g(D)\) and \(h(D)\) are polynomial operators with constant coefficients for every function \(u(t)\)
10 What is the substitution rule of polynomial differential operators?
10.1 Front
What is the substitution rule of polynomial differential operators?
10.2 Back
\(p(D) e^{at} = p(a) e^{at}\)
11 Expand this expression?
11.1 Front
Expand this expression?
\(p(D)e^{at} u(t)\)
11.2 Back
\(e^{at} p(D+a)u(t)\), by the exponential-shift rule
12 Expand this expression?
12.1 Front
Expand this expression?
\(D^3 e^{-t} \sin(t)\)
Using several methods
12.2 Back
Solution using the exponential-shift rule (and binomial theorem)
\begin{align*} D^3 e^{-t} \sin(t) &= e^{-t}(D-1)^3 \sin(t)\\\ &= e^{-t}(D^3 -3D^2 + 3D -1) \sin(t) \\\ &= e^{-t}(2 \cos(t) + 2 \sin(t)) \end{align*}
Solution using the substitution rule
We can write \(e^{-t} \sin(t) = \operatorname{Im}(e^{(-1 + i)t})\)
\begin{align*} D^3e^{(-1 + i)t} &= (-1 + i)^3 e^{(-1 + i)t} \\\ &= (2+2i)e^t(\cos(t) + i \sin(t))\\\ &= e^t(2 \cos(t) + 2 \sin(t)) \text{ Getting the imaginary part} \end{align*}
13 Can we use this expansion if \(c\) and \(a\) are complex numbers?
13.1 Front
Can we use this expansion if $c$ and $a$ are complex numbers?
\(D(c e^{at}) = c a e^{at}\)
And the others rules of differential operator
13.2 Back
Yes, you can. Also, you can apply the rules and arguments for differential operators
14 What is a linear time invariant “LTI”?
14.1 Front
What is a linear time invariant “LTI”?
14.2 Back
On linear ODE \(p(D)x = q(t)\) where \(p(D)\) is a constant coefficient operator, you can apply the time invariance of \(p(D)\) and you can say for another ODE \(p(D)y = q(t-c)\) that its particular solution is \(y(t) = x(t-c)\)
15 In which cases can I say that \(y(t) = x(t - c)\) for …
15.1 Front
In which cases can I say that $y(t) = x(t - c)$ for …
the ODE \(p(D) y = q(t-c)\) and \(y(t)\) is a solution of \(p(D)y = q(t)\)
15.2 Back
In case that \(p(D)\) is a constant coefficient operator
It’s called Linear Time Invariant operator
16 Which guess solution could be used for getting the particular solution?
16.1 Front
Which guess solution could be used for getting the particular solution?
\(y’’ + y’ + y = 2xe^x\)
16.2 Back
You can try \(y_p = a_1 xe^x + a_2 e^x\)
- \(y_p’ = a_1(x+1) e^x + a_2 e^x\)
- \(y_p’’ = a_1(x+2) e^x + a_2e^x\)
- \(2xe^x = (a_1(x+2) e^x + a_2e^x) + (a_1(x+1) e^x + a_2 e^x) + (a_1 xe^x + a_2
e^x) = 3a_1xe^x + (3a_1 + 3a_2)e^x\)
- \(3a_1 = 2 \implies a_1 = 2/3\)
- \((3a_1 + 3a_2) = 0 \implies 2 + 3 a_2 \implies a_2 = -2/3\)
17 Which guess solution could be used for getting the particular solution?
17.1 Front
Which guess solution could be used for getting the particular solution?
\(y^{(4)} - 2 y’’ + y = xe^x\)
17.2 Back
- \(p(s) = s^4 -2 s^2 + 1 = (s^2 - 1)^2\)
- so \(p(1)=0\) repeated root (order 2)
- guess: \(y_p = x^2(Ax + B)e^{x}\)
18 Graph the amplitude in terms of \(\omega\) of this ODE
18.1 Front
Graph the amplitude in terms of $\omega$ of this ODE
\(x’’ + \omega_0^2 x = F_0 \cos(\omega t)\)
Graph also the response when \(\omega = \omega_0\)
18.2 Back
Solving the ODE with complex replacement, characteristic polynomial and Exponential Response Formula (ERF)
- \({\displaystyle x_p = \frac{F_0 \cos(\omega t)}{\omega_0^2 - \omega^2}}\) when \(\omega_0 \neq \omega\)
- \({\displaystyle x_p = \frac{F_0 t \sin(\omega_0 t)}{2 \omega_0}}\) when \(\omega_0 = \omega\)
\({\displaystyle A(\omega) = \abs{\frac{F_0}{\omega_0^2 - \omega_2}}}\)
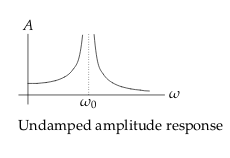
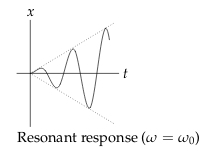
19 What happens when \(\omega\) are really close to \(\omega_{0}\) in this system?
19.1 Front
What happens when $\omega$ are really close to $\omega_{0}$ in this system?
\((D^2 + \omega_0^2)x = F_0 \cos(\omega t)\)
ERF: \({\displaystyle x_p(t) = \frac{F_0 \cos(\omega t)}{\omega_0^2 - \omega^2}}\)
Study how is the response when \(\omega \to \omega_0\)
19.2 Back
In this case the amplitude of the output is bigger than the amplitude of the input, but the period is the same.
When \(\omega = \omega_0\), it the case on pure resonance, and the RRF is completely different \({\displaystyle x_p(t) = \frac{F_0 t \sin(\omega t)}{2 \omega_0}}\)
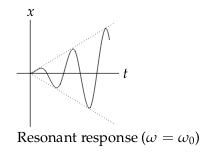
We can analyse what happens with another particular solution (getting a part from the complementary solution associated to homogeneous model), and study it what happens when \(\omega \to \omega_0\)
\({\displaystyle x_p(t) = \frac{F_0 \cos(\omega t)}{\omega_0^2 - \omega^2} - \frac{F_0 \cos(\omega_0 t)}{\omega_0^2 - \omega^2}}\)
\({\displaystyle \lim_{\omega \to \omega_0} x_p = \lim_{\omega \to \omega_0} \frac{- F_0 t \sin(\omega t)}{- 2 \omega} = \frac{F_0 t \sin(\omega_0 t)}{2 \omega_0}}\)
This is the response to the resonance.
20 How is the graph of this solution when \(\omega \to \omega_{d}\)
20.1 Front
How is the graph of this solution when $\omega \to \omega_{d}$
\({\displaystyle x_p(t) = \frac{F_0 \cos(\omega t)}{\omega_0^2 - \omega^2} - \frac{F_0 \cos(\omega_0 t)}{\omega_0^2 - \omega^2}}\)
20.2 Back
You need to use the trigonometric identify \(\cos(B) - \cos(A) = 2 \sin(\frac{A-B}{2}) \sin(\frac{A+B}{2})\)
For this case \({\displaystyle \cos(\omega t) - \cos(\omega_0 t) = 2 \sin(\frac{t(\omega - \omega_0)}{2}) \sin(\frac{t(\omega + \omega_0)}{2})}\)
As \(\omega \to \omega_{0}\),
\({\displaystyle \frac{F_0 \sin(\frac{t(\omega - \omega_0)}{2})}{\omega_0^2 - \omega^2}}\), describe a very low frequency function with really big amplitude.
And inside, there is the function \(\sin(t \omega_0)\)
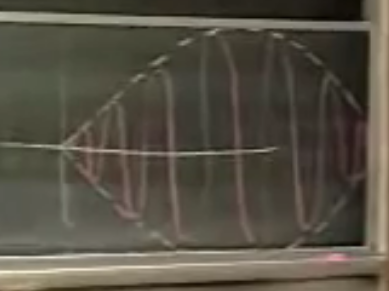
21 How can we proof that this particular solution is valid for this system?
21.1 Front
How can we proof that this particular solution is valid for this system?
\(x_p(t) = \frac{t e^{at}}{p’(a)}\), is a solution of \(p(D)x = e^{at}\) and \(p(a) = 0\)
21.2 Back
We can write \(p(D) = q(D)(D - a)\), where \(q(a) \neq 0\) because of \(p(D)\) could be factor by \((D - a)\)
So, \(p’(D) = q’(D)(D-a) + q(D)\), so \(p’(a) = q’(a)(a - a) + q(a) = q(a)\)
\begin{align*} p(D)x_p(t) &= p(D) \frac{t e^{at}}{p’(a)} \\\ &= \frac{e^{at}}{p’(a)} p(D + a)t \\\ &= \frac{e^{at}}{p’(a)} q(D + a) D t \\\ &= \frac{e^{at}}{q(a)} q(D + a) 1 \\\ &= \frac{e^{at}}{q(a)} q(a) = e^{at} \end{align*}
22 Which is the value of this expression?
22.1 Front
Which is the value of this expression?
\(p(D + a)1\), where \(a\) is a constant
22.2 Back
\(p(a)\)