- Captured On
- Source
- [[https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-ii-second-order-constant-coefficient-linear-equations/damped-harmonic-oscillators/index.htm][Damped Harmonic Oscillators | Unit II: Second Order Constant Coefficient
Linear Equations | Differential Equations | Mathematics | MIT OpenCourseWare]]
1 What is a damped sinusoid equation?
1.1 Front
What is a damped sinusoid equation?
Write the general form
1.2 Back
\(y(t) = A e^{- \lambda t} \cos(\omega t - \phi)\)
2 What is the basic solutions of DE is we get \(z(t)\) with complex exponential?
2.1 Front
What is the basic solutions of DE is we get $z(t)$ with complex exponential?
\(z(t) = e^{(a + ib)t} = e^{at}(\cos(bt) + i \sin(bt))\)
2.2 Back
Using the Real Solution Theorem, the two basic solutions are the real and imaginary part os \(z_1\)
- \(e^{at} \cos(bt)\)
- \(e^{at} \sin(bt)\)
3 Which are the solutions if the roots of characteristic polynomial are repeated?
3.1 Front
Which are the solutions if the roots of characteristic polynomial are repeated?
In a second order constant coefficients linear equation, for example \(p(s) = (s+2)^2\)
3.2 Back
\(r = -2\) as a repeated root, the only exponential solution is \(e^{-2t}\). But, we can looking for another solution which is not a constant multiple of \(e^{-2t}\). Given by \(te^{-2t}\)
\(x(t) = c_1e^{-2t} + c_2 t e^{-2t} = e^{-2t} (c_1 + c_2t)\)
4 Suppose the roots of a certain homogeneous constant coefficient linear equation are
4.1 Front
Suppose the roots of a certain homogeneous constant coefficient linear equation are
\(3, 4, 4, 4, 5 \pm 2i, 5 \pm 2i\)
Give the general real solutions to the equation
4.2 Back
Basic solutions
- \(e^{3t}\)
- \(e^{4t}\)
- \(te^{4t}\)
- \(t^2e^{4t}\)
- \(e^{5t} \cos(2t)\)
- \(e^{5t} \sin(2t)\)
- \(te^{5t} \cos(2t)\)
- \(te^{5t} \sin(2t)\)
For each repeated root we added a multiple \(t\) to the basic solutions
Using superposition, the general solution is
\(x(t) = c_1 e^{3t} + c_2 e^{4t} + c_3 te^{4t} + c_4 t^2e^{4t} + c_5 e^{5t} \cos(2t) + c_6 e^{5t} \sin(2t) + c_7 t e^{5t} \cos(2t) + c_8 t e^{5t} \sin(2t)\)
5 What is the order of the DE if we get 8 roots?
5.1 Front
What is the order of the DE if we get 8 roots?
5.2 Back
The order of the differential equation is \(8\)
6 How can get a real solution if get complex superposition solution?
6.1 Front
How can get a real solution if get complex superposition solution?
We get 2 complex roots in the characteristic polynomial, and we get \(z_1(t) = e^{(a + ib)t}\) and \(z_2(t) = e^{(a - ib)t}\).
We say that \(x(t) = C_1 e^{(a + ib)t} + C_2 e^{(a - ib)t}\)
Define \(C_1\) and \(C_2\) and write a complete form
6.2 Back
If \(x(t)\) is a real solutions \(C_1\) and \(C_2\) must be complex numbers. If you need to get only the real part we could expand the solution and get it, but it’ll be to long.
If we change \(i \to -i\) and the formula is the same, we can say that this is a real number, so
\(x(t) = C_1 e^{(a + ib)t} + C_2 e^{(a - ib)t} = \bar{C_1} e^{(a - ib)t} + \bar{C_2} e^{(a + ib)t}\) this implies that
\(\bar{C_1} = C_2\) and \(\bar{C_2} = C_1\), so the real solution must be in the form
\(x(t) = (c + id) e^{(a + ib)t} + (c - id) e^{(a - ib)t}\)
This form in science and engineering
7 Can we apply the uniqueness theorem to a second order DE?
7.1 Front
Can we apply the uniqueness theorem to a second order DE?
7.2 Back
No, the uniqueness theorem as stated only applies to first order equations
8 What are the values \(r\) for this equation?
8.1 Front
What are the values $r$ for this equation?
\(r^2 + k = 0\)
8.2 Back
\(r = \pm \sqrt{-k} = \pm i \sqrt{k}\)
9 Given the solution get its DE?
9.1 Front
Given the solution get its DE?
\(y = c_1 + c_2x\)
9.2 Back
\(y’ = 2\) and \(y’’=0\), so this implies \(a = 1\), \(b=c\), on its characteristic polynomial \(ar^2 + br + c = 0\)
10 What is the model of the damped harmonic oscillator?
10.1 Front
What is the model of the damped harmonic oscillator?
Write the DE
10.2 Back
\(m\ddot{x} + b\dot{x} + kx = 0\)
Where \(m \gt 0\), \(b \geq 0\), \(k \gt 0\)
11 What are the differences between damped harmonic oscillator and simple harmonic oscillator?
11.1 Front
What are the differences between damped harmonic oscillator and simple harmonic oscillator?
11.2 Back
Damped harmonic oscillator: \(m\ddot{x} + b\dot{x} + kx = 0\)
When \(b=0\) it has a pure sinusoidal solution and this DE is called simple harmonic oscillator
12 How can we study damped harmonic oscillator system?
12.1 Front
How can we study damped harmonic oscillator system?
Which method?
12.2 Back
The roots of characteristic polynomial
13 What are the solutions of a simple harmonic oscillator?
13.1 Front
What are the solutions of a simple harmonic oscillator?
13.2 Back
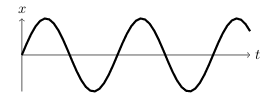
DE: \(m\ddot{x} + kx = 0\)
\(x(t) = c_1 \cos(\omega t) + c_2 \sin(\omega t) = A\cos(\omega t - \phi)\), where \(\omega = \sqrt{k/m}\)
The output is pure sinusoid
14 What kind of response are there in a harmonic oscillator system?
14.1 Front
What kind of response are there in a harmonic oscillator system?
Estimate its values for each kind of response
14.2 Back
\(m\ddot{x} + b\dot{x} + kx = 0\), where \(m \gt 0, b \geq 0, k \gt 0\)
It has characteristic equation
\(ms^2 + bs + k = 0\)
with characteristic roots
\({\displaystyle \frac{-b \pm \sqrt{b^2 - 4mk}}{2m}}\)
- underdamping
- \(b^2 \lt 4mk\) (\(b\) is small relative to \(m\) and \(k\))
- overdamping
- \(b^2 \gt 4mk\) (\(b\) is large relative to \(m\) and \(k\))
- critical damping
- \(b^2 = 4mk\) (\(b\) is just between over and underdamping)
15 What does mean that a harmonic oscillator system is underdamping?
15.1 Front
What does mean that a harmonic oscillator system is underdamping?
\(m\ddot{x} + b\dot{x} + kx = 0\)
Solve it and give solutions
15.2 Back
Where characteristic roots are \({\displaystyle \frac{-b \pm \sqrt{b^2 - 4mk}}{2m}}\)
If \(b^2 \lt 4mk\) the square root are negative (characteristic root are non-real), \(b\) is relatively small
Let \({\displaystyle \omega_d = \frac{\sqrt{\abs{b^2 - 4mk}}}{2m}}\), then
- characteristic root are
- \({\displaystyle \frac{-b}{2m} \pm i \omega_d}\)
- Complex exponential solutions:
- \({\displaystyle e^{(-b/2m + i\omega_d)t}}\)
- \({\displaystyle e^{(-b/2m - i\omega_d)t}}\)
- Basic real solutions:
- \({\displaystyle e^{-bt/2m} \cos(\omega_d t)}\)
- \({\displaystyle e^{-bt/2m} \sin(\omega_d t)}\)
- General real solution
- \({\displaystyle c_1 e^{-bt/2m} \cos(\omega_d t) + c_2 e^{-bt/2m} \sin(\omega_d t) = A e^{-bt/2m} \cos(\omega_d t - \phi)}\)
16 What does mean physically that a harmonic oscillator system is underdamping?
16.1 Front
What does mean physically that a harmonic oscillator system is underdamping?
\(m\ddot{x} + b\dot{x} + kx = 0\), which solution is \(A e^{-bt/2m} \cos(\omega_d t - \phi)\)
16.2 Back
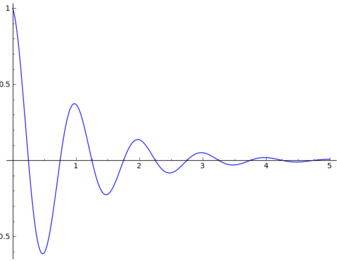
When \(b=0\) the response is a sinusoid. Damping is a frictional force, so it generates heat and dissipates energy. When the damping constant \(b\) is small we would expect the system still oscillate, but with decreasing amplitude as its energy is converted to heat.
Over time it should come to rest at equilibrium. In the solution, the factor \(\cos(\omega_d t - \phi)\) shows the oscillation. The exponential factor \(e^{-bt/2m}\) has a negative exponent and therefore gives the decaying amplitude. As \(t \to \infty\), the exponential goes asymptotically to \(0\), so \(x(t)\) also goes asymptotically to its equilibrium position \(x=0\)
17 What is the \(\omega_{d}\) in a harmonic oscillator system?
17.1 Front
What is the $\omega_{d}$ in a harmonic oscillator system?
\(m\ddot{x} + b\dot{x} + kx = 0\), which solution is \(A e^{-bt/2m} \cos(\omega_d t - \phi)\)
17.2 Back
Is the damped angular (or circular) frequency, also it’s called pseudo-frequency of \(x(t)\). But \(\omega_d\) is not periodic and only periodic functions have a frequency. Nonetheless, \(x(t)\) does oscillate, crossing \(x=0\) twice each pseudo-period.
\({\displaystyle \omega_d = \frac{\sqrt{\abs{b^2 - 4mk}}}{2m}}\)
18 What does mean that a harmonic oscillator system is overdamping?
18.1 Front
What does mean that a harmonic oscillator system is overdamping?
\(m\ddot{x} + b\dot{x} + kx = 0\)
Solve it and give solutions
18.2 Back
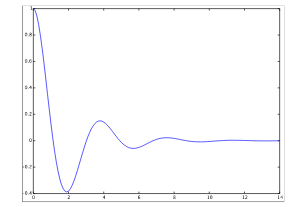
It’s the case when the characteristic roots are distinct real roots. If \(b^2 \gt 4mk\), the term under square root is positive. In order for \(b^2 \gt 4mk\) the damping constant \(b\) must be relatively large.
The roots are both negative, since \(b^2 - 4mk \lt b^2\) the square root is less than \(b\) and therefore the root \(-b + \sqrt{b^2 - 4mk} \lt 0\)
- Characteristic roots
- \({\displaystyle r_1 = \frac{-b + \sqrt{b^2 - 4mk}}{2m}}\)
- \({\displaystyle r_2 = \frac{-b - \sqrt{b^2 - 4mk}}{2m}}\)
- Exponential solutions
- \({\displaystyle e^{r_1t}}\)
- \({\displaystyle e^{r_2t}}\)
- General solution
- \({\displaystyle x(t) = c_1 e^{r_1t} + c_2 e^{r_2t}}\)
19 What does mean physically that a harmonic oscillator system is overdamping?
19.1 Front
What does mean physically that a harmonic oscillator system is overdamping?
\(m\ddot{x} + b\dot{x} + kx = 0\), where its solution is \(x(t) = c_1 e^{r_1t} + c_2 e^{r_2t}\)
19.2 Back
When the damping is large the frictional force is so great that the system can’t oscillate. It might sound odd, but an unforced overdamping harmonic oscillator does not oscillate. Since both exponents are negative every solution in this case goes asymptotically to the equilibrium \(x=0\)
At the top of many doors is a spring to make them shut automatically. The spring is damped to control the rate at which the door closes. If the damper is strong enough, so that the spring is overdamping, then the door just settles back to the equilibrium position (i.e. the closed position) without oscillating - which is usually what is wanted in this case.
20 What does mean that a harmonic oscillator system is critical damping?
20.1 Front
What does mean that a harmonic oscillator system is critical damping?
\(m\ddot{x} + b\dot{x} + kx = 0\)
Solve it and give solutions
20.2 Back
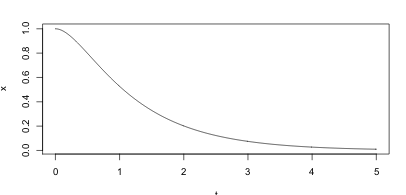
It’s the case when the characteristic roots are repeated. If \(b^2 = 4mk\) then the term under the square root is \(0\)
- Repeated characteristic roots
- \({\displaystyle \frac{-b}{2m}}\)
- Basic solutions
- \({\displaystyle x_1(t) = e^{-bt/2m}}\)
- \({\displaystyle x_2(t) = te^{-bt/2m}}\)
- General solution
- \({\displaystyle x(t) = e^{-bt/2m} (c_1 + c_2t)}\)
21 What does mean physically that a harmonic oscillator system is critical damping?
21.1 Front
What does mean physically that a harmonic oscillator system is critical damping?
21.2 Back
As in the overdamping case, this does not oscillate. It is worth noting that for a fixed \(m\) and \(k\), choosing \(b\) to be the critical damping value gives the fastest return of the system to its equilibrium position.
In engineering design this is often a desirable property. This can be seen by considering the roots, but we will not go through the algebra that show this.
22 What are the differences between overdamping and critical damping harmonic oscillator?
22.1 Front
What are the differences between overdamping and critical damping harmonic oscillator?
22.2 Back
The critical damping response gives the fastest return of the system to its equilibrium position.
23 What happens if we increases the damping constant in a harmonic oscillator?
23.1 Front
What happens if we increases the damping constant in a harmonic oscillator?
\(m\ddot{x} + b\dot{x} + kx = 0\)
23.2 Back
If \(b\) goes up, then the damped angular frequency goes down. It that means that the frequency of oscillation will be slowed, until critical damping or over damping.
24 Suppose that \(x(t)\) is a solution of the equation \(m\ddot{x} + b\dot{x} + kx=0\)
24.1 Front
Suppose that $x(t)$ is a solution of the equation $m\ddot{x} + b\dot{x} + kx=0$
where \(x(t) = e^{-t/2} \cos(3t)\)
What are the exponential solutions (solution of the form \(e^{\alpha t}\))?
24.2 Back
- \(e^{(-1/2 + 3i)t}\)
- \(e^{(-1/2 - 3i)t}\)
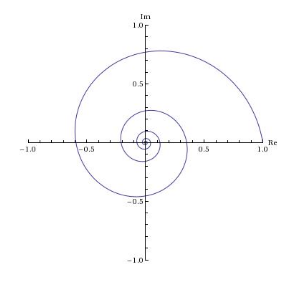
25 How can we graph exponential solutions curve in the complex plane?
25.1 Front
How can we graph exponential solutions curve in the complex plane?
for example, \(z(t) = e^{(-1/2 + 3i)t}\)
25.2 Back
Using parametric functions
- \(x(t) = e^{-t/2} \cos(3t)\)
- \(y(t) = e^{-t/2} \sin(3t)\)
26 Let \(\omega \gt 0\). A damped sinusoid \(x(t) = Ae^{-at}\cos(\omega t)\)
26.1 Front
Let $\omega \gt 0$. A damped sinusoid $x(t) = Ae^{-at}\cos(\omega t)$
With “pseudo-period” \(2\pi / \omega\)
What is the spacing between successive maxima of \(x(t)\)?. Is it always the same, or does it differ from one successive pair of maxima to the next?
26.2 Back
The extrema of \(x(t)\) occur when \(\dot{x}(t) = 0\)
- \({\displaystyle 0 = Ae^{-at}(-a \cos(\omega t) - \omega \sin(\omega t))}\)
- \({\displaystyle \omega \sin(\omega t) = -a \cos(\omega t)}\)
- \({\displaystyle \tan(\omega t) = - \frac{a}{\omega}}\)
The maxima occur at every other such \(t\), and the spacing between successive maxima is twice the period of \(\tan(\omega t)\), which is just the pseudo-period \(2 \pi/\omega\). This is always the same since it doesn’t depend on \(t\) or \(x\)
27 Let damped sinusoid \(Ae^{-at}\cos(\omega t)\) where \(\omega \gt 0\)
27.1 Front
Let damped sinusoid $Ae^{-at}\cos(\omega t)$ where $\omega \gt 0$
How could we get the \(a\) value?
27.2 Back
Suppose that 2 successive maxima occur at \(t = t_0\) and \(t = t_1\), that means that \(\cos(\omega t_1) = \cos(\omega t_0 + 2 \pi) = \cos(\omega t_0)\)
Getting the ratio \(\frac{x(t_1)}{x(t_0)} = e^{a(t_0 - t_1)}\)
\({\displaystyle a = \frac{\ln(x(t_1)) - \ln(x(t_0))}{t_0 - t_1}}\)
28 What is a normalized pair of solutions of a damping oscillator system?
28.1 Front
What is a normalized pair of solutions of a damping oscillator system?
28.2 Back
- \(x_1\) is a solution with IVP \(x_1(0) = 1\) and \(\dot{x_1}(0) = 0\)
- \(x_2\) is a solution with IVP \(x_2(0) = 0\) and \(\dot{x_2}(0) = 1\)
29 From this normalized solutions, how can we get any other solution from IVP?
29.1 Front
From this normalized solutions, how can we get any other solution from IVP?
- \(x_1\) is a solution with IVP \(x_1(0) = 1\) and \(\dot{x_1}(0) = 0\)
- \(x_2\) is a solution with IVP \(x_2(0) = 0\) and \(\dot{x_2}(0) = 1\)
New IVP \(x(0) = 2\) and \(\dot{x}(0) = 3\)
29.2 Back
\(x = 2 \cdot x_1 + 3 x_2\)
30 What are 2 different independent solutions for a ODE?
30.1 Front
What are 2 different independent solutions for a ODE?
For example \(y_1\) and \(y_2\)
30.2 Back
These 2 solutions are different if \(y_1 \neq c y_2\) and \(y_2 \neq c' y_1\). There is an exception if one of them are \(y_1 = 0\) and \(y_2 \neq 0\)
31 Is the derivative a linear operator with respect to sum?
31.1 Front
Is the derivative a linear operator with respect to sum?
31.2 Back
Let \(y(x)\) be a function and \(c\) a constant
- \((y_1 + y_2)’ = y_1’ + y_2’\)
- \((cy)’ = c y’\)