- Captured On
- Source
- First Order Constant Coefficient Linear ODE’s | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is a constant coefficient First ODE?
1.1 Front
What is a constant coefficient First ODE?
1.2 Back
\(\dot{y} + ky = q(t)\), where \(k\) is a constant
2 What is the solution of a constant coefficient First ODE?
2.1 Front
What is the solution of a constant coefficient First ODE?
\(\dot{y} + ky = q(t)\), where \(k\) is a constant
2.2 Back
\({\displaystyle y(t) = e^{-kt} \biggl( \int e^{kt} q(t) \dd{t} + c \biggr) = e^{-kt} \int e^{kt} q(t) \dd{t} + ce^{-kt}}\)
The general solution is \(y(t) = y_p(t) + cy_h(t)\)
3 What is the particular solution of a constant coefficient first ODE?
3.1 Front
What is the particular solution of a constant coefficient first ODE?
\(\dot{y} + ky = q(t)\), where \(k\) is a constant
3.2 Back
\(y_p(t) = e^{-kt} \int e^{kt} q(t) \dd{t}\)
4 What is the homogeneous solution of a constant coefficient first ODE?
4.1 Front
What is the homogeneous solution of a constant coefficient first ODE?
\(\dot{y} + ky = q(t)\), where \(k\) is a constant
4.2 Back
\(y_h(t) = ce^{-kt}\)
5 Explain what happens when \(k>0\) in a constant coefficient first ODE?
5.1 Front
Explain what happens when \(k>0\) in a constant coefficient first ODE?
\(\dot{y} + ky = q(t)\), where \(k\) is a constant
5.2 Back
It models exponential decay, when the input is \(0\) the system response is \(y(t) = ce^{-kt}\), which decays exponentially to \(0\) as \(t \to \infty\)
In the general solution, the term \(ce^{-kt}\) is called transient because it goes to \(0\). And the term \({\displaystyle e^{-kt} \int e^{kt}q(t) \dd{t}}\) is called the steady-state or long term solution.
The value of \(c\) is determined by the initial value of \(y(0)\). The initial value only affects the transient term and not the long-term behaviour. So, every solution goes asymptotically to the steady-state as \(t \to \infty\)
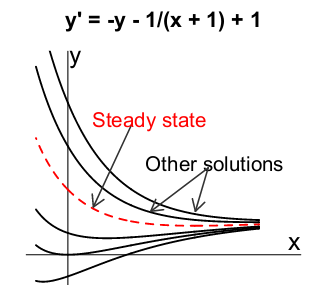
6 Draw a graph with the solutions of a constant coefficient first ODE?
6.1 Front
Draw a graph with the solutions of a constant coefficient first ODE?
\(\dot{y} + ky = q(t)\), where \(k>0\) is a constant
6.2 Back