- Captured On
- Source
- Sinusoidal Functions | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is a sinusoidal function equation?
1.1 Front
What is a sinusoidal function equation?
1.2 Back
\(f(t) = A \cos(\omega t - \phi)\)
2 What is the sinusoidal oscillation equation?
2.1 Front
What is the sinusoidal oscillation equation?
2.2 Back
\(f(t) = A \cos(\omega t - \phi)\)
3 What is the sinusoidal signal equation?
3.1 Front
What is the sinusoidal signal equation?
3.2 Back
\(f(t) = A \cos(\omega t - \phi)\)
4 What does represent this equation?
4.1 Front
What does represent this equation?
\(f(t) = A \cos(\omega t - \phi)\)
Explain each term too
4.2 Back
A sinusoidal function (or sinusoidal oscillation or sinusoidal signal) which is a cosine function which has been amplified by \(A\), shifted by \(\phi / w\), and compressed by \(w\)
5 What is the amplitude of the sinusoidal function?
5.1 Front
What is the amplitude of the sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
5.2 Back
\(A > 0\): how high the graph of \(f(t)\) rises above the \(t\text{-axis}\) at its maximum values
6 What is the phase lag of the sinusoidal function?
6.1 Front
What is the phase lag of the sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
6.2 Back
\(\phi\), the value of \(wt\) for which the graph has its maximum
- \(\phi = 0\), the graph has the position of \(\cos(\omega t)\)
- \(\phi = \pi /2\) it has the position of \(\sin(wt)\)
7 What is the time delay or time lag of the sinusoidal function?
7.1 Front
What is the time delay or time lag of the sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
7.2 Back
\(\tau = \phi / w\), how far the \(x\text{-axis}\) the graph of \(\cos(\omega t)\) has been shifted to make the graph of \(f(t)\)
\(A \cos(\omega t - \phi) = A \cos(w(t - \phi/w))\)
8 What is the angular frequency of the sinusoidal function?
8.1 Front
What is the angular frequency of the sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
8.2 Back
\(\omega\) is the number of complete oscillations \(f(t)\) makes in a time interval of length \(2\pi\). Number of radians per unit time
9 What is the frequency of sinusoidal function?
9.1 Front
What is the frequency of sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
9.2 Back
\(\nu = \omega / 2\pi\), the number of complete oscillations the graph makes in a time interval of length \(1\). Number of cycles per unit time
10 What is the period of the sinusoidal function?
10.1 Front
What is the period of the sinusoidal function?
\(f(t) = A \cos(\omega t - \phi)\)
10.2 Back
\(P = 2 \pi / \omega = 1 / \nu\)
11 Get information from this graph
11.1 Front
Get information from this graph
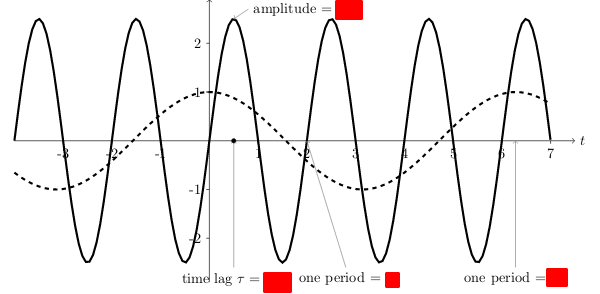
Extract the function
11.2 Back
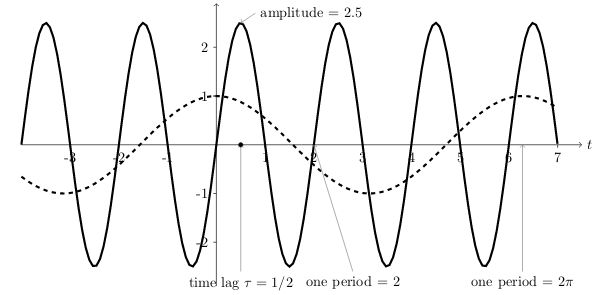
- \(A = 2.5\)
- \(\tau = \frac{1}{2}\)
- \(T = 2\)
- \(T = \frac{2 \pi}{\omega} \implies \omega = \frac{2\pi}{T} = \pi\)
- \(\tau = \frac{\phi}{w} \implies \phi = \tau \omega = \frac{\pi}{2}\)
- \(f(t) = 2.5 \cos(\pi t - \pi/2)\)
12 What is the sinusoidal identity?
12.1 Front
What is the sinusoidal identity?
12.2 Back
The sum of two sinusoidal functions of the same frequency is another sinusoidal function with that frequency
\(a \cos(\omega t) + b\sin(\omega t) = A \cos(\omega t - \phi)\)
Where
- \(A = \sqrt{a^2 + b^2}\)
- \(\phi = atan2(b,a)\)
- \(a + bi = A e^{i\phi}\)
13 How can we get the combination of these 2 sinusoidal functions?
13.1 Front
How can we get the combination of these 2 sinusoidal functions?
\(a \cos(\omega t) + b \sin(\omega t)\)
13.2 Back
Using the right triangle, where
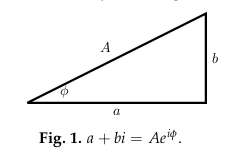
- \(a = A \cos (\phi)\)
- \(b = A \sin (\phi)\)
- \(\phi = atan2(b,a)\)
- \(a + ib = Ae^{i\phi}\)
\begin{align*} a \cos(\omega t) + b \sin(\omega t) &= A \cos(\phi) \cos(\omega t) + A \sin(\phi)\sin(\omega t)\\\ &=A(\cos(\phi) \cos(\omega t) + \sin(\phi)\sin(\omega t)) \\\ &=A(\cos(\omega t - \phi)) , \text{using cosine addition formula} \end{align*}
14 Which properties has any linear combination of \(\cos(\omega t)\) and \(\sin(\omega t)\)?
14.1 Front
Which properties has any linear combination of \(\cos(\omega t)\) and \(\sin(\omega t)\)?
14.2 Back
- It’s a sinusoidal function too
- Its period is \({\displaystyle \frac{2\pi}{\omega}}\)
15 What is the amplitude-phase form of sinusoidal function?
15.1 Front
What is the amplitude-phase form of sinusoidal function?
15.2 Back
\(A \cos(\omega t - \phi)\)
16 What is the rectangular or Cartesian form of sinusoidal function?
16.1 Front
What is the rectangular or Cartesian form of sinusoidal function?
16.2 Back
\(a \cos(\omega t) + b \sin(\omega t)\)
17 Proof that equation using vectors?
17.1 Front
Proof that equation using vectors?
\(a \cos(\omega t) + b \sin(\omega t) = A \cos(\omega t - \phi)\)
17.2 Back
Where \(a \cos(\omega t) + b \sin(\omega t)\) can we write as the dot product \(\ev{a,b} \cdot \ev{\cos \theta, \sin \theta}\)
Using dot product computation
\(\abs{\ev{a,b} \cdot 1 \cdot \cos (\omega t - \phi)}\)
18 Proof this equation using complex numbers?
18.1 Front
Proof this equation using complex numbers?
\(a \cos(\omega t) + b \sin(\omega t) = A \cos(\omega t - \phi)\)
18.2 Back
We can write \(a \cos(\omega t) + b \sin(\omega t)\) as \(\operatorname{Re}((a -ib)(\cos(\omega t) + i\sin(\omega t)))\)
\(\phi = atan2(b, a)\)
Using Euler’s formula \(\operatorname{Re}(\sqrt{a^2 + b^2} e^{- i \phi} e^{i \omega t}) = \operatorname{Re}(\sqrt{a^2 + b^2}e^{i(\omega t - \phi)})\)
\(\sqrt{a^2 + b^2} \cos (\omega t - \phi)\)