- Captured On
- Source
- Complex Arithmetic and Exponentials | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is a complex number?
1.1 Front
What is a complex number?
1.2 Back
A complex number is an expression of the form \(a + ib\)
2 When can we say that 2 complex number are equals?
2.1 Front
When can we say that 2 complex number are equals?
\(a + ib = c + id\), where \(a,b,c,d\) are real numbers
2.2 Back
When \(a = c\) and \(b = d\)
3 What are the real and imaginary part of a complex number?
3.1 Front
What are the real and imaginary part of a complex number?
\(a + ib\)
3.2 Back
- \(a = \operatorname{Re}(a + ib)\)
- \(b = \operatorname{Im}(a + ib)\)
4 What represent the symbol \(i\) in a complex number?
4.1 Front
What represent the symbol \(i\) in a complex number?
4.2 Back
\(i = \sqrt{-1}\), so \(i^2 = -1\)
5 How can we sum 2 complex numbers
5.1 Front
How can we sum 2 complex numbers
\((a + ib) + (c + id)\)
5.2 Back
\((a + c) + i(b + d)\)
6 How can we multiply 2 complex numbers?
6.1 Front
How can we multiply 2 complex numbers?
\((a + ib)(c + id)\)
6.2 Back
\((ac - bd) + i(ad + bc)\)
7 How can we divide 2 complex numbers?
7.1 Front
How can we divide 2 complex numbers?
\({\displaystyle \frac{a + ib}{c + id}}\)
7.2 Back
Assuming that \(c + id \neq 0\), and using complex conjugate of \(c + id\)
\({\displaystyle \frac{a + ib}{c + id} \cdot \frac{c - id}{c - id} = \frac{ac + bd}{c^2 + d^2} + i \frac{bc - ad}{c^2 + d^2}}\)
8 What is a complex conjugate and why is useful?
8.1 Front
What is a complex conjugate and why is useful?
\(z = a + ib\)
8.2 Back
Complex conjugate of \(z\) is \(\overline{z} = a - ib\), note that \(\overline{z}z = a^2 + b^2\).
It’s useful for compute the division between 2 complex numbers
9 What is the value of \(\overline{z}z\) where \(z\) is a complex number?
9.1 Front
What is the value of \(\overline{z}z\) where \(z\) is a complex number?
\(z = a + ib\)
9.2 Back
\(\overline{z}z = a^2 + b^2 = \abs{z}^2\)
10 What is the absolute value of a complex number?
10.1 Front
What is the absolute value of a complex number?
\(z = a + ib\)
10.2 Back
It’s the same as the modulus of \(z\)
\(\abs{z} = \abs{a + ib} = \sqrt{a^2 + b^2}\)
11 What is the modulus of a complex number?
11.1 Front
What is the modulus of a complex number?
\(z = a + ib\)
11.2 Back
It’s the same as the absolute value of \(z\)
\(\abs{z} = \abs{a + ib} = \sqrt{a^2 + b^2}\)
12 What is the complex plane?
12.1 Front
What is the complex plane?
12.2 Back
It’s the plane where are represented a complex number \(a + ib\) in Cartesian coordinates, where it’s a point at \((a,b)\)
13 How can we represent a complex number in polar coordinates?
13.1 Front
How can we represent a complex number in polar coordinates?
\(a + ib\)
13.2 Back
- \(a = x = r \cos(\theta)\)
- \(b = y = r \sin(\theta)\)
Assuming \(a + ib \neq 0\), \(a + ib = r (\cos(\theta) + i \sin(\theta))\), and using the Euler’s formula \(a + ib = r e^{i\theta}\)
Where \(r = \abs{a + ib} = \sqrt{a^2 + b^2}\), and \(\theta = \operatorname{arg}(a + ib)\), where \(0 \neq \theta < 2\pi\)
\({\displaystyle \theta = \arctan(\frac{b}{a})}\), being aware the sign of the \(a\) and \(b\) for setting correctly \(\theta\) in its quadrant
14 What is the argument of a complex number?
14.1 Front
What is the argument of a complex number?
\(a + ib\)
14.2 Back
It is the polar angle \(\theta\) in polar coordinates, \(\theta = \operatorname{arg}(a + ib)\)
15 What is the Euler’s Formula?
15.1 Front
What is the Euler’s Formula?
15.2 Back
\(e^{i\theta} = \cos \theta + i \sin \theta\)
16 How can we justify the Euler’s Formula?
16.1 Front
How can we justify the Euler’s Formula?
16.2 Back
Using the infinite series from the definition of \(e\)
\({\displaystyle e^t = 1 + \frac{t}{1!} + \frac{t^2}{2!} + \frac{t^3}{3!} + \dots}\)
Substituting \(t\) for \(i\theta\)
\begin{align*} e^{i\theta} &= \biggl(1 - \frac{\theta}{2!} + \frac{\theta^4}{4!} - \dots \biggr) + i \biggl(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \dots \biggr)\\\ &= \cos(\theta) + i \sin(\theta) \end{align*}
in view of the infinite series representations for \(\cos(\theta)\) and \(\sin(\theta)\)
It’s not a proof because the series expansion of \(e^t\) is valid when \(t\) is a real number. It’s formally compatible with the series expansions for the exponential, sine and cosine functions.
17 Why is it useful the complex number in polar representation?
17.1 Front
Why is it useful the complex number in polar representation?
17.2 Back
It reduces the complexity of complex number multiplication and division. Using the form \(re^{i\theta}\) you can follow the exponential addition rules as the real exponential
18 How can we multiply these terms?
18.1 Front
How can we multiply these terms?
\(r_1e^{i\theta_1} \cdot r_2e^{i\theta_2}\)
18.2 Back
\(r_1 r_2 e^{i(\theta_1 + \theta_2)}\)
Multiply the absolute values and add the angles.
19 What is it the reciprocal of this term?
19.1 Front
What is it the reciprocal of this term?
\({\displaystyle \frac{1}{re^{i\theta}}}\)
19.2 Back
\({\displaystyle \frac{1}{r} e^{-i\theta}}\)
20 How can we divide these terms?
20.1 Front
How can we divide these terms?
\({\displaystyle \frac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}}}\)
20.2 Back
\({\displaystyle \frac{r_1}{r_2} e^{i(\theta_1 - \theta_2)}}\)
Divide by its absolute value and subtract its angle
21 What is the DeMoivre’s formula?
21.1 Front
What is the DeMoivre’s formula?
21.2 Back
\((\cos \theta + i \sin \theta)^n = \cos (n\theta) + i \sin(n\theta)\)
It’s the special case when \(r=1\)
22 Expand this formula
22.1 Front
Expand this formula
\((\cos \theta + i \sin \theta)^n\)
22.2 Back
\(\cos (n\theta) + i \sin(n\theta)\)
23 Expand this formula
23.1 Front
Expand this formula
\(\cos (n\theta) + i \sin(n\theta)\)
23.2 Back
\((\cos \theta + i \sin \theta)^n\)
24 Express \((1 + i)^{6}\) in Cartesian form
24.1 Front
Express \((1 + i)^{6}\) in Cartesian form
24.2 Back
\({\displaystyle (1 + i)^6 = (\sqrt{2} e^{i\pi/4})^6 = (\sqrt{2})^6 e^{i 6 \pi / 4} = 8 e^{i3 \pi / 2} = -8i}\)
25 Express this formula in polar form
25.1 Front
Express this formula in polar form
\({\displaystyle \frac{1 + i \sqrt{3}}{\sqrt{3} + i}}\)
25.2 Back
\({\displaystyle \frac{1 + i \sqrt{3}}{\sqrt{3} + i} = \frac{2 e^{i \pi/3}}{2 e^{i \pi / 6}} = e^{i \pi/6}}\)
26 Express this formula in complex numbers?
26.1 Front
Express this formula in complex numbers?
\(a \cos(\lambda t) + b \sin(\lambda t)\)
26.2 Back
where \(a + ib = A e^{i \phi}\)
\begin{align*} a \cos(\lambda t) + b \sin(\lambda t) &= \operatorname{Re}((a - ib) \cdot (\cos(\lambda t) + i \sin(\lambda t))) \\\ &= \operatorname{Re}(Ae^{-i \phi} \cdot e^{i \lambda t})\\\ &= \operatorname{Re}(A e^{i (\lambda t - \phi)}) = A \cos (\lambda t - \phi) \end{align*}
27 Write this expression in polar representation
27.1 Front
Write this expression in polar representation
\(a - ib\)
27.2 Back
\(A e^{-i \theta}\), where \(A = \sqrt{a^2 + b^2}\) and \(\theta = \arctan (b/a)\)
28 Justify that \(e^{i\theta_{1}}\cdot e^{i\theta_{2}} = e^{i \theta_{1}+ \theta_{2}}\)
28.1 Front
Justify that \(e^{i\theta_{1}}\cdot e^{i\theta_{2}} = e^{i \theta_{1}+ \theta_{2}}\)
Can we use the exponential law with complex exponential?
28.2 Back
\begin{align*} e^{i\theta_1}\cdot e^{i\theta_2} &= (\cos \theta_1 + i \sin \theta_1) \cdot (\cos \theta_2 + i \sin \theta_2)\\\ &= \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 + i (\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2) \\\ &= \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)\\\ &= e^{i(\theta_1 + \theta_2)} \end{align*}
29 Justify this equation
29.1 Front
Justify this equation
\({\displaystyle \dv{\theta} e^{i \theta} = i e^{i \theta}}\), and that \(y(0) = 1\)
29.2 Back
\begin{align*} \dv{\theta} e^{i \theta} &= \dv{\theta}(\cos \theta + i \sin \theta)\\\ &= \dv{\theta}(\cos \theta) + i \dv{\sin \theta}\\\ &= -\sin \theta + i \cos \theta \\\ &= i(\cos \theta + i \sin \theta) \\\ &= i e^{i\theta} \end{align*}
\({\displaystyle e^{i0} = \cos 0 + i \sin 0} = 1 + i0 = 1\)
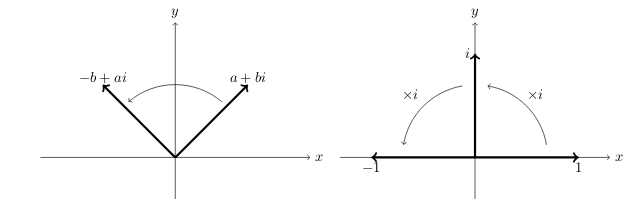
30 What effect has multiply by \(i\) a complex number in the complex plane?
30.1 Front
What effect has multiply by \(i\) a complex number in the complex plane?
\(i(a + ib)\)
30.2 Back
\(i(a + ib) = -b +ia\)
Which is rotated by 90 degrees counterclockwise
31 If \(\overline{z}=z\), what does that tell us about the value \(z=a+ib\)?
31.1 Front
If \(\overline{z}=z\), what does that tell us about the value \(z=a+ib\)?
31.2 Back
\(a - ib = - (a + ib) \implies a = -a = 0\)
32 Which is the definition of an exponential to an arbitrary complex power?
32.1 Front
Which is the definition of an exponential to an arbitrary complex power?
\(e^{a + ib}\)
32.2 Back
\(e^{a + ib} = e^a e^{ib} = e^a (\cos (b) + i \sin(b))\)
33 What is the real part of an exponential to a complex number?
33.1 Front
What is the real part of an exponential to a complex number?
\(\operatorname{Re}(e^{a + ib})\)
33.2 Back
\(e^a \cos(b)\)
34 What is the imaginary part of an exponential to a complex number?
34.1 Front
What is the imaginary part of an exponential to a complex number?
\(\operatorname{Im}(e^{a + ib})\)
34.2 Back
\(e^a \sin (b)\)
35 How can you express cosine in terms of complex exponential?
35.1 Front
How can you express cosine in terms of complex exponential?
\(\cos(x)\)
35.2 Back
\({\displaystyle \cos(x) = \operatorname{Re}(e^{ix}) = \frac{1}{2} (e^{ix} + e^{-ix})}\)
36 How can you express sine in terms of complex exponential?
36.1 Front
How can you express sine in terms of complex exponential?
\(\sin(x)\)
36.2 Back
\({\displaystyle \sin(x) = \operatorname{Im}(e^{ix}) = \frac{1}{2i}(e^{ix} - e^{-ix})}\)
37 Express \(\cos^{3}(x)\) in terms of the functions \(\cos(nx)\), for suitable \(n\)
37.1 Front
Express \(\cos^{3}(x)\) in terms of the functions \(\cos(nx)\), for suitable \(n\)
\(\cos^3(x)\)
37.2 Back
Using \(\cos(x) = \frac{1}{2} (e^{ix} + e^{-ix})\) and the binomial theorem
\begin{align*} \cos^3(x) &= \frac{1}{2^3} (e^{ix} + e^{-ix})^3 \\\ &= \frac{1}{8}(e^{3x} + 3e^{ix} + 3e^{-ix} + e^{-3ix}) \\\ &= \frac{1}{4}(\frac{1}{2}(e^{3x} + e^{-3ix}) + \frac{1}{2}(3e^{ix} + 3e^{-ix})) \\\ &= \frac{1}{4} \cos(3x) + \frac{3}{4} \cos(x) \end{align*}
38 Express \(e^{x}\cos(2x)\) in terms of exponential
38.1 Front
Express \(e^{x}\cos(2x)\) in terms of exponential
38.2 Back
Using: \(e^x e^{i2x} = e^x (\cos(2x) + i\sin(2x))\)
\(e^x \cos(2x) = \operatorname{Re}(e^{(1+2i)x})\)
39 What is the derivative of \(e^{(a + ib)x}\) with respect to \(x\)?
39.1 Front
What is the derivative of \(e^{(a + ib)x}\) with respect to \(x\)?
\(D(e^{(a + ib)x})\)
39.2 Back
\(D(e^{(a + ib)x}) = (a + ib)e^{(a + ib)x}\)
40 What is the integral of \(e^{(a + ib)x}\) with respect to \(x\)?
40.1 Front
What is the integral of \(e^{(a + ib)x}\) with respect to \(x\)?
\({\displaystyle \int e^{(a + ib)x} dx}\)
40.2 Back
\({\displaystyle \int e^{(a + ib)x} dx = \frac{1}{a + ib} e^{(a + ib)x}}\)
41 Minimize this formula
41.1 Front
Minimize this formula
\({\displaystyle \operatorname{Re}(\frac{1}{1 + 2i} e^{(1 + 2i)x})}\)
41.2 Back
\({\displaystyle \biggl(\frac{1}{5} - \frac{2}{5}i \biggr) (e^x \cos(2x) + ie^x \sin(2x)) = \frac{1}{5} e^x \cos(2x) + \frac{2}{5} e^x \sin(2x)}\)
42 How can we get the \(n\text{th}\) roots of unity
42.1 Front
How can we get the \(n\text{th}\) roots of unity
\(z^n = 1\)
Explain the process
42.2 Back
- Use polar representation for both sides, using all possible polar angles
- \(r^n e^{in\theta} = 1 \cdot e^{2k\pi i}\), \(k = 0, \pm 1, \pm 2, \dots\)
- Equating the absolute value and polar angles
- \(r^n = 1\)
- \(n \theta = 2k\pi\), \(k = 0, \pm 1, \pm 2, \dots\)
- Where we can conclude
- \(r = 1\)
- \({\displaystyle \theta = \frac{2k \pi}{n}}\), \(k = 0, 1, 2, \dots, n-1\)
- If we add \(an\), an integer multiple of \(n\), to \(k\), we get the same
complex number
- \({\displaystyle \theta ‘= \frac{2(k + an) \pi}{n} = \theta + 2a\pi}\)
- \(e^{i\theta ‘} = e^{i\theta}\), since \(e^{2a\pi i} = (e^{2 \pi i})^2\)
- Conclusion
- the \(n-\text{th}\) roots of \(1\) are the numbers \(e^{2k\pi i / n}\), \(k = 0, 1, 2, \dots, n-1\)
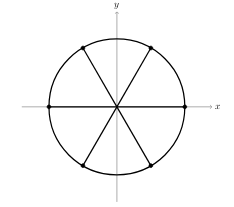
43 How can we represent \(n-\text{th}\) roots of unity?
43.1 Front
How can we represent \(n-\text{th}\) roots of unity?
In the complex plane
43.2 Back
- All lies on the unit circle in the complex plane, since have absolute value \(1\)
- Evenly spaced around the unit circle, starting with the root \(z=1\)
- Angle between 2 consecutive roots is \(2\pi / \theta\)
Case \(n=6\), solutions to the equation \(z^6 = 1\)
44 What are the \(n-\text{th}\) roots of unity?
44.1 Front
What are the \(n-\text{th}\) roots of unity?
Using \(\zeta\) notation
44.2 Back
The \(n\text{-th}\) roots of \(1\) are \(1, \zeta, \zeta^2, \zeta^3, …, \zeta^{n-1}\), where \(\zeta = e^{2\pi i / n}\)
45 How can we represent a complex number using the maximum number of complex angles?
45.1 Front
How can we represent a complex number using the maximum number of complex angles?
For \(1\) and \(re^{i\theta}\)
45.2 Back
Using \(e^{i 2\pi k} = 1\), multiplying by \(1\):
- \(1 \cdot e^{i 2\pi k}\), for \(k = 0, \pm 1, \pm 2, \dots\)
- \(r e^{i\theta} e^{i 2\pi k} = r e^{i(2\pi k + \theta)}\)
46 How can we get \(n-\text{th}\) roots of any complex number \(w\)?
46.1 Front
How can we get \(n-\text{th}\) roots of any complex number \(w\)?
\(w = re^{i\theta}\), where \(\theta = \operatorname{Arg}(w), 0 \leq \theta < 2\pi\)
46.2 Back
- \(z^n = w = re^{i\theta}\)
- \(p^n e^{in\phi} = r e^{i\theta} e^{i 2\pi k}\), for \(k = 0, \pm 1, \pm 2, \dots\)
- Conclusion
- \(p = \sqrt[n]{r}\)
- \(\phi = \frac{\theta + 2 \pi k}{n}\) for \(k = 0, 1, 2, \dots, n-1\)
So \(z = \sqrt[n]{r} e^{i(\theta + 2\pi k)/n}\)
the \(n-\text{th}\) roots of \(1\) are the numbers \(\sqrt[n]{r}e^{i (\theta + 2k\pi )/ n}\), \(k =0, 1, 2, \dots, n-1\)
You can write the roots as \(\sqrt[n]{w} = z_0, z_0 \zeta, z_0 \zeta^2, \dots, z_0 \zeta^{n-1}\), where \(z_0 = \sqrt[n]{r}e^{i \theta / n}\)
47 What is \(\zeta\) in the roots of a complex number?
47.1 Front
What is \(\zeta\) in the roots of a complex number?
47.2 Back
\(\zeta = e^{i 2 \pi / n}\), where \(\zeta^n = 1\)
48 Check that all numbers in this series satisfy \(z^{n}=w\)
48.1 Front
Check that all numbers in this series satisfy \(z^{n}=w\)
\(\sqrt[n]{w} = z_0, z_0 \zeta, z_0 \zeta^2, \dots, z_0 \zeta^{n-1}\), where \(z_0 = \sqrt[n]{r}e^{i \theta / n}\)
48.2 Back
- \((z_0 \zeta^i)^n = z_0^n \zeta^{ni} = z_0^n \cdot 1^{i} = w\), where \(w = z^n\)
49 Which is the value of \(z^{-n}\) of a complex number?
49.1 Front
Which is the value of \(z^{-n}\) of a complex number?
49.2 Back
\(z^{-n} = r^{-n} e^{-i n \theta}\)
50 What is the value of \((-i)^{2}\)?
50.1 Front
What is the value of \((-i)^{2}\)?
50.2 Back
\((-i) \cdot (-i) = 1 (i) \cdot i = -1\)