- Captured On
- Source
- First Order Linear ODE’s | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is a first order linear ODE?
1.1 Front
What is a first order linear ODE?
Write the standard form
1.2 Back
In the unknown function \(x = x(t)\)
\({\displaystyle A(t) \dv{x}{t} + B(t) x(t) = C(t)}\)
As \(A(t) \neq 0\), we can simplify the equation by dividing by \(A(t)\)
Standard form: \({\displaystyle \dv{x}{t} + p(t)x(t) = q(t)}\)
2 When can we say that a first order linear ODE is homogeneous?
2.1 Front
When can we say that a first order linear ODE is homogeneous?
Using the standard form
2.2 Back
\(\dv{x}{t} + p(t) x(t) = 0\)
In any other case is inhomogeneous
3 Why I need to use the standard form for first order linear ODE?
3.1 Front
Why I need to use the standard form for first order linear ODE?
3.2 Back
Because you can get completely wrong solutions. Some function with wrong signal can produce completely different results.
4 Which of the following are linear ODE’s?
4.1 Front
Which of the following are linear ODE’s?
- \(\dot{x} + x^2 = t\)
- \(\dot{x} = (t^2 + 1)(x-1)\)
- \(\dot{x} + x = t^2\)
4.2 Back
Only the 2 and 3 equations are linear
5 Describe this linear ODE in terms of System and Signals?
5.1 Front
Describe this linear ODE in terms of System and Signals?
\(\dot{x} - rx = q(t)\)
Is the model of a bank account
5.2 Back
- System: left-hand side of the equation, the bank
- Input signal / input: right-hand side, it’s the outside influence on
the system
- Signal is a function of \(t\)
- Output signal / System response: it’s how the system responds to the
input signal and yields the function \(x(t)\)
- Is the solution \(x(t)\)
These are not mathematical terms
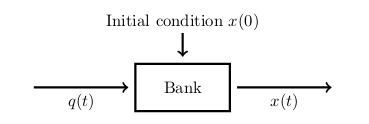
6 Draw the block diagram for these linear ODE?
6.1 Front
Draw the block diagram for these linear ODE?
\(\dot{x} - rx = q(t)\)
Is the model of a bank account
6.2 Back
7 What is the superposition principle for linear ODEs?
7.1 Front
What is the superposition principle for linear ODEs?
Consider the linear ODE \(\dot{y} + p(t) y = q(t)\)
7.2 Back
For any given input \(q(t)\) that has output \(y(t)\), \(q \leadsto y\) (read input \(q\) leads to output \(y\))
Let \(q_1\) and \(q_2\) be input signals, and \(c_1\) and \(c_2\) be constant, so we can say that \(c_1 q_1(t) + c_2q_2(t)\) is a superposition of \(q_1\) and \(q_2\).
It’s also called linear combination of \(q_1\) and \(q_2\)
If \(q_1 \leadsto y_1\) and \(q_2 \leadsto y_2\) then \(c_1 q_1 + c_2 q_2 \leadsto c_1 y_1 + c_2 y_2\)
8 Why is valid the superposition principle?
8.1 Front
Why is valid the superposition principle?
equation: \(\dot{y} + p(t)y = q(t)\)
8.2 Back
If \(q_1 \leadsto y_1\) and \(q_2 \leadsto y_2\) then \(c_1 q_1 + c_2 q_2 \leadsto c_1 y_1 + c_2 y_2\)
It’s valid because the ODE is linear.
\({\displaystyle \dv{t} (c_1 y_1 + c_2 y_2) + p(c_1 y_1 + c_2 y_2) = c_1 (\dot{y_1} + p y_1) + c_2 (\dot{y_2} + p y_2) = c_1 q_1 + c_2 q_2}\)
9 Find lots of solution to…
9.1 Front
Find lots of solution to…
\(\dot{x} + 2x = 1 + e^{-2t}\)
9.2 Back
Write the input as \(1 + e^{-2t} = 1 + e^{-2t} + c \cdot 0\)
Using the superposition principle, \(x(t) = 1 \cdot \frac{1}{2} + c \cdot e^{-2t}\), where any value of the parameter \(c\) is a solution
10 Is this equation a linear ODE?
10.1 Front
Is this equation a linear ODE?
\(\frac{\dot{y}}{y} = t^2\)
10.2 Back
Yes, it’s, you can multiple both sides by \(y\)
\(\dot{y} - t^2 y = 0\)
11 How can we show that for this nonlinear ODE we cannot use superposition principle?
11.1 Front
How can we show that for this nonlinear ODE we cannot use superposition principle?
\(\dot{y} + y^2 = q(t)\)
11.2 Back
First, we’ll get 2 equation and them use the superposition principle to get an a contradiction.
- \(\dot{y_1} + y_1^2 = 1\)
- \(\dot{y_2} + y_2^2 = t\)
Using the superposition principle, \(y = y_1 + y_2\), so we need to proof that \(\dot{y} + y^2 = 1 + t\)
\({\displaystyle \dv{t} (y_1 + y_2) + (y_1 + y_2)^2 = \dot{y_1} + \dot{y_2} + y_1^2 + y_2^2 + 2 y_1 y_2 = (1 + t) + 2 y_1 y_{2} \neq (1 + t)}\)
Hence, we get a contradiction