- Captured On
- Source
- Geometric Methods | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 What is a direction field
1.1 Front
What is a direction field
for the equation \(y’ = f(x,y)\)
1.2 Back
For each point \((x,y)\) of the plane is drawn a little segment whose slope is \(f(x,y)\)
For example: \({\displaystyle \dv{y}{x} = 2x}\)
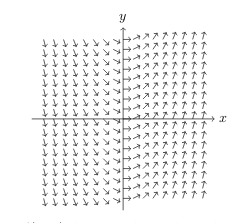
2 How can we draw a direction field by hand?
2.1 Front
How can we draw a direction field by hand?
for the equation \(y’ = f(x,y)\)
2.2 Back
- Draw in lightly (or in dashed lines) the isoclines for \(y’ = f(x,y)\)
- Family of curves given by \(f(x,y) = m\), where \(m\) is constant
- Along the isocline, the line segments all have the same slope \(m\)
- Draw a solid line curves which are at each point tangent to the line segment at that point, this curve is a integral curve (solution curves) for the direction field
3 What is a isocline?
3.1 Front
What is a isocline?
for \(y’ = f(x,y)\)
3.2 Back
These are the one-parameter family of curves given by the equations \(f(x,y) = m\), where \(m\) is constant
Along this line, all segments in a direction field has the same slope
“iso-cline” = “equal slope”
4 What is the direction field for \(y’ = x - y\)?
4.1 Front
What is the direction field for \(y’ = x - y\)?
4.2 Back
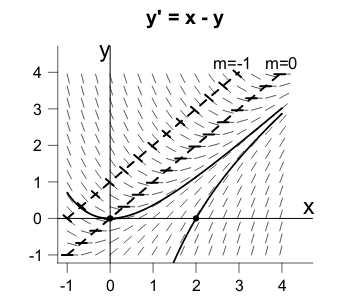
Isocline for
- \(m = -1\), \(-1 = x - y \implies y = x + 1\)
- \(m = 0\), \(0 = x-y \implies y = x\), at this line the slope is horizontal
5 What is a integral curve for the direction field?
5.1 Front
What is a integral curve for the direction field?
for the equation \(y’ = f(x,y)\)
5.2 Back
It’s a line which are at each point tangent to the line segment at that point in a direction field. These line segment are given by isoclines
Are the graphs of the solution to \(y’ = f(x,y)\)
6 Can 2 integral curve cross each other?
6.1 Front
Can 2 integral curve cross each other?
6.2 Back
No, they can’t because of the Existence and Uniqueness theorem
7 Can 2 integral curves be tangent each other?
7.1 Front
Can 2 integral curves be tangent each other?
Can 2 integral curves touch each other?
7.2 Back
No, they can’t because of the Existence and Uniqueness theorem
8 Which is the Existence and Uniqueness Theorem for ODEs?
8.1 Front
Which is the Existence and Uniqueness Theorem for ODEs?
for the equation \(y’ = f(x,y)\)
8.2 Back
For any \((a,b)\) in the region where \(f\) is defined, \(y’= f(x,y)\) has exactly one solution (one and only one) such that \(y(a) = b\)
The theorem can fail if \(f(x,y)\) is not continuous at \((a,b)\)
9 Must \(y(x)\) be defined for all \(x\) to use Existence and Uniqueness Theorem for ODEs?
9.1 Front
Must \(y(x)\) be defined for all \(x\) to use Existence and Uniqueness Theorem for ODEs?
9.2 Back
No, it may only exist for \(x\) near \(a\)
10 What does happen if \(f(x,y)\) is not continuous at \((a,b)\)?
10.1 Front
What does happen if \(f(x,y)\) is not continuous at \((a,b)\)?
Tip: Referee to Existence and Uniqueness Theorem for ODE’s
10.2 Back
The might be many solution curves or no solution curves that pass through the point \((a,b)\)
11 Can we say that Existence and Uniqueness Theorem fails for this DE?
11.1 Front
Can we say that Existence and Uniqueness Theorem fails for this DE?
\(x y’ = 1 - y\), which solution is \(y = 1 - Cx\)
11.2 Back
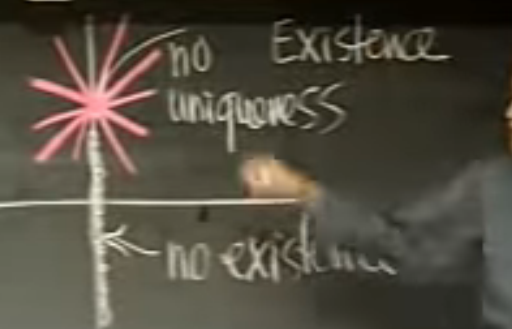
If we write the DE in standard format \(y’ = f(x,y)\), then we see that \(\dv{y}{x} = \frac{1-y}{x}\), where we can see that this DE is not defined for \(x = 0\)
So, the theorem is correct, only that the domain reduced
12 What is a nullcline?
12.1 Front
What is a nullcline?
12.2 Back
It’s a isocline with \(m=0\), it’s where the \(y’\) is \(0\)
13 Why are important fences and funnels in isoclines?
13.1 Front
Why are important fences and funnels in isoclines?
13.2 Back
Are used to find out for certain where trajectories go at scales you can’t see
- small scales
- largest scales (off the screen) that are relevant to long-term behaviour
14 What kinds of fences are there at isocline diagrams?
14.1 Front
What kinds of fences are there at isocline diagrams?
for the equation \(y’ = f(x,y)\)
14.2 Back
- Lower fence
- Is a curve that ‘blocks’ an integral curve from crossing from above
- To find such a fence look for a curve so that all the direction field elements along the curve point up from it
- The lower curve is the lower fence
- Any integral curve crossing the fence must cross tangent to the slope field cannot cross it from above
- \(y = L(x)\) such that \(L’(x) < f(x, L(x))\)
- The slope of the curve is always less than the slope of the direction field at each point
- Upper fence
- Is a curve that blocks integral curves from crossing from below
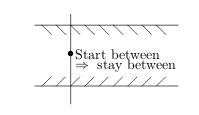
15 How can you construct pieces of fences?
15.1 Front
How can you construct pieces of fences?
15.2 Back
- Using pieces of isocline
- Using straight line segments
16 Do we need to defined a fence for all \(x\)?
16.1 Front
Do we need to defined a fence for all \(x\)?
16.2 Back
No, you could define them only on an interval. The best sort of fences for understanding long-term behaviour are defined for all \(x \geq c\), for a fairly small constant \(c\)
17 What happens if a integral curve can’t cross an integral curve itself?
17.1 Front
What happens if a integral curve can’t cross an integral curve itself?
17.2 Back
Is both an upper and a lower fence
18 Which are the fences of this equation?
18.1 Front
Which are the fences of this equation?
\(y’ = y^2 - x\)
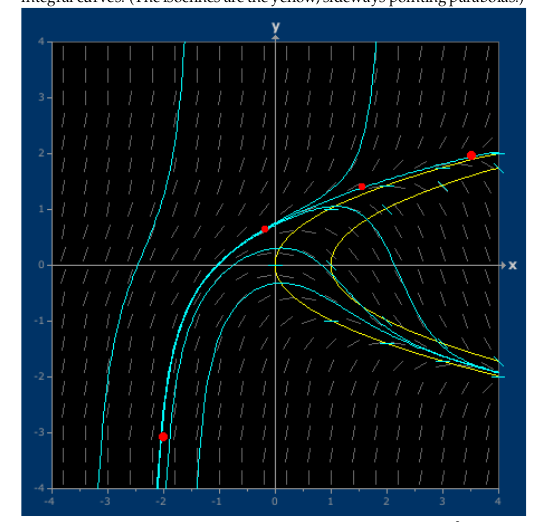
18.2 Back
- Lower fence: is the bottom half of the isocline \(m=0\) for \(x\) large enough
- Upper fence: is the bottom half of the isocline \(m=-1\) for \(x\) large enough
Look carefully you’ll see one of the integral curves crossing it from above near \(x=1\), so \(m=-1\) is an upper fence only for large values of \(x\)
19 What is a funnel?
19.1 Front
What is a funnel?
for the equation \(y’ = f(x,y)\)
19.2 Back
Consists of a pair of fences; one lower fence \(L(x)\) and one upper fence \(U(x)\)
- For \(x\) large the lower fence is below the upper fence \(L(x) < U(x)\)
- Two fences come together asymptotically
- \(U(x) - L(x)\) is small for large \(x\)
The integral curves that end up between them are trapped there
20 Define the funnel for this equation?
20.1 Front
Define the funnel for this equation?
\(y’ = y^2 - x\)
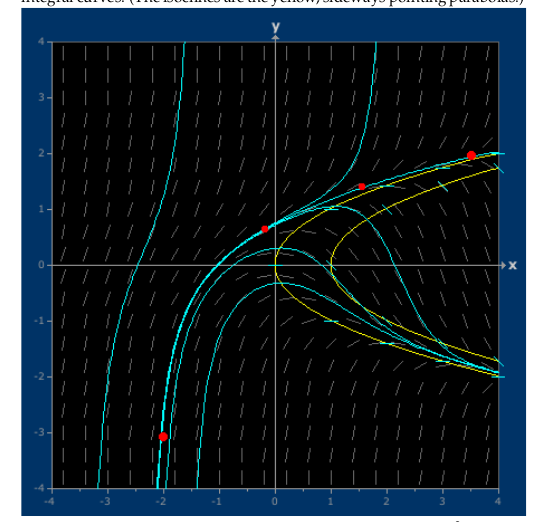
20.2 Back
For \(x > 2\) (large \(x\)), the isocline \(m=0\) (lower fence) and \(m=-1\) (upper fence) act as a funnel
Bottom half of the isocline \(m=0\) is \(y = - \sqrt{x}\) and the bottom half of \(m=-1\) is \(y = - \sqrt{x - 1}\)
For the solutions between them have the highly accurate estimates
\({\displaystyle - \sqrt{x} < y(x) < - \sqrt{x - 1}}\)
which is valid for large \(x\)
21 Could 2 parallel lines form a funnel?
21.1 Front
Could 2 parallel lines form a funnel?
21.2 Back
No, because they are parallel, at constant distance one apart
To be a funnel, the 2 curves must come asymptotically together as \(x\) gets larger
22 What is a separatrix?
22.1 Front
What is a separatrix?
22.2 Back
Is an integral curve such that integral curves above it behave entirely differently from integral curves below it as \(x\) increases to infinity.
23 If a integral curve seems to be a straight line, how can we get the solution equation?
23.1 Front
If a integral curve seems to be a straight line, how can we get the solution equation?
\(y’ = x - 2y\)
23.2 Back
Looking for what \(m\) and \(b\) is \(y = mx + b\) a solution
\({\displaystyle m = \dv{y}{x} = x - 2y = x - 2(mx + b) = (1 - 2m)x - 2b}\)
Two polynomials in \(x\) can only the same for all \(x\) (over the reals) if they have the same coefficients. Equate coefficients of the powers of \(x\) to get two equations in two unknowns that must be satisfied simultaneously.
- \(m = 2b\)
- \(0 = 1 -2m\)
So, \(m = 1/2\) and plugging in \(m\) in the first equation \(b = -1/4\)
Solution: \({\displaystyle y = \frac{1}{2} x - \frac{1}{4}}\)
24 When can we say that a isocline is a solution of DE?
24.1 Front
When can we say that a isocline is a solution of DE?
for \(y’ = 2x + y\)
24.2 Back
The isocline curves are of the form \(y = -2x + m\), if \(y’=-2 = 2x + y\)
We see, that the isocline \(y = -2x -2\) can get from the solution \(y = -2x - 2\)
25 What happens if integral curve cannot cross a isocline?
25.1 Front
What happens if integral curve cannot cross a isocline?
25.2 Back
It’s possible that this isocline it’s a solution for the DE