- Captured On
- Source
- Basic DE’s and Separable Equations | Unit I: First Order Differential Equations | Differential Equations | Mathematics | MIT OpenCourseWare
1 Can be \(e^{at}=0\)?
1.1 Front
Can be \(e^{at}=0\)?
1.2 Back
Never
2 Write a sketch of the graph
2.1 Front
Write a sketch of the graph
\(y=e^t\)
2.2 Back
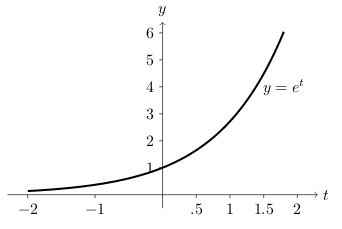
3 Write a sketch of the graph
3.1 Front
Write a sketch of the graph
\(y=e^{-t}\)
3.2 Back
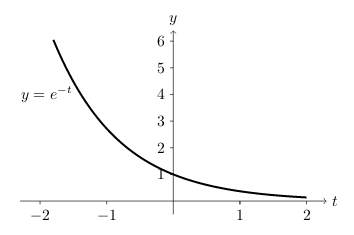
4 What is a n-parameter family of functions?
4.1 Front
What is a n-parameter family of functions?
Let \(x(t)\) be the family of functions
4.2 Back
The antiderivative of a function produces a family of functions, but some times can have more than 1 variable
- 1-parameter family of functions
- \(x(t) = t^3/3 + c\)
- 2-parameter family of functions
- \(x(t) = c_1e^{-t} + c_2e^{-7t}\)
5 Which is the physicists’ notation for derivative respect to time \(t\)?
5.1 Front
Which is the physicists’ notation for derivative respect to time \(t\)?
1st and 2nd derivative
5.2 Back
1st derivative: \(\dot{x}\)
2nd derivative: \(\ddot{x}\)
6 Explain with words what is a differential equation
6.1 Front
Explain with words what is a differential equation
6.2 Back
Is an equation expressing a relation between a function and its derivatives
\(\ddot{x} + 8\dot{x} + 7x = 0\)
7 What is the order of a differential equation
7.1 Front
What is the order of a differential equation?
7.2 Back
Is the order of the largest derivative appearing in it
8 What does mean solving a differential equation?
8.1 Front
What does mean solving a differential equation?
8.2 Back
Finding a function that satisfies the equation. For many equations it can be hard or impossible to find a solution.
Check a proposed solution is easy, you can check it by substitution
9 How can we parametrize the set of solutions of a differential equation?
9.1 Front
How can we parametrize the set of solutions of a differential equation?
For example: \(\ddot{x} = 2t\)
9.2 Back
\(x(t) = \frac{t^3}{3} + c_1t + c_2\)
Integrating twice and remembering to include the constants of integrations
You can choose any value for \(c_1\) and \(c_2\)
10 Why is useful to have initial conditions?
10.1 Front
Why is useful to have initial conditions?
For differential equations
10.2 Back
For getting a specific functions from the family of functions given by the solution of the differential equation.
11 What does mean this DE?
11.1 Front
What does mean this DE?
\(\dot{y} = ay\)
Explain it in words
11.2 Back
The rate of change of \(y\) is proportional to \(y\)
12 Write as DE the next equation?
12.1 Front
Write as DE the next equation?
The rate of change of \(y\) is proportional to \(y\)
12.2 Back
- \(\dot{y} = ay\)
- \({\displaystyle \dv{y}{t} = ay(t)}\)
- \(y’ = ay\)
- \(\dot{y} - ay = 0\)
13 Which is the solution of this DE?
13.1 Front
Which is the solution of this DE?
\(\dot{y} = ay\)
13.2 Back
\(y(t) = Ce^{at}\)
Because of the exponential in the solution is said to model exponential growth (when \(a>0\)) or decay (when \(a < 0\)). The constant \(a\) is known as the growth or decay constant
14 What is a lost solution of a DE?
14.1 Front
What is a lost solution of a DE?
Solving the DE by separation of variables
14.2 Back
After separate by variables an DE, the equation is not defined for some values. So, we need to control that the solution not include this values as a solution
15 What does mean IVP at differential equations?
15.1 Front
What does mean IVP at differential equations?
15.2 Back
Initial value problem (IVP)
16 What does mean ODE at differential equations?
16.1 Front
What does mean ODE at differential equations?
16.2 Back
Ordinary differential equation (ODE)
17 What is the doubling time for natural growth/decay system?
17.1 Front
What is the doubling time for natural growth/decay system?
17.2 Back
Is the time it takes for the population to double. This cannot be read off directly from the infinitesimal information afforded by the differential equation, as it requires knowledge of the long-term behaviour of the system. You need to solve the DE.
By definition, the doubling time is the time \(T\) for which \(x(T) = 2x(0)\)
For example, for \(x(t) = Ce^{kt}\), \({\displaystyle Ce^{kT} = 2C \implies T = \frac{\ln{2}}{k}}\)
Doubling time is only used when the rate of growth is positive. If the rate of growth is negative, this would be a system with a positive “natural rate of decay” \(-k\), and a defined concept of a half-life
It’s ok to calculate doubling time use an implicit (potentially arbitrary) choice made of initial time \(t=0\) because the time it takes for the population of a natural growth system to double does not depend on count-off time. For example, \(x(t+T) = 2x(t)\) for all \(t\)
18 What is the half-life for natural growth/decay system?
18.1 Front
What is the half-life for natural growth/decay system?
18.2 Back
Is the time it takes for the population to decrease by half. This cannot be read off directly from the infinitesimal information afforded by the differential equation, as it requires knowledge of the long-term behaviour of the system. You need to solve the DE.
By definition, the half-life is the time \(T\) for which \(x(T) = \frac{1}{2} x(0)\).
As \(x(t) = Ce^{kt}\), \({\displaystyle e^{kT} = \frac{1}{2} e^{0} \implies kT = \ln(1/2) = - \ln(2)}\), so \({\displaystyle T = - \frac{\ln{2}}{k}}\)
It’s ok to calculate half-life time using an implicit (potentially arbitrary) choice made of initial time \(t=0\) because the time it takes for the population of a natural growth system to double does not depend on count-off time. For example, \(x(t+T) = 1/2 x(t)\) for all \(t\)
19 If the rate of growth/decay were zero…
19.1 Front
If the rate of growth/decay were zero…
It makes sense the concepts of doubling time/half-life
19.2 Back
No,
20 What steps do we need to do for getting a general solution for DE?
20.1 Front
What steps do we need to do for getting a general solution for DE?
For example, \({\displaystyle \dv{x}{t} = kx -a}\) for arbitrary \(a,k\)
20.2 Back
- If \(k=0\), DE is \({\displaystyle \dv{x}{t} = -a \implies x(t) = -at + C}\), \(x(0) = C\)
- If \(k \neq 0\)
- \({\displaystyle \frac{\dd{x}}{x - a/k} = k \dd{t}}\)
- Let \(u = x - a/k \implies \pdv{u}{t} = \pdv{x}{t}\)
- \({\displaystyle \frac{\dd{u}}{u} = k \dd{t} \implies u(t) = Ce^{kt}}\)
- \({\displaystyle x(t) = Ce^{kt} + \frac{a}{k}}\)
- Initial value is \(x(0) = C + a/k\)
- Missing solution \(x \equiv a/k\)
21 How can we find a constant solution for a DE?
21.1 Front
How can we find a constant solution for a DE?
For example, \(\dv{x}{t} = kx-a\)
21.2 Back
There is no variances along the changes of time (equilibrium)
Constant solution: \(\dv{x}{t} \equiv 0\), in these case \(kx = a\)
- If \(k=0\), then \(a = 0\)
- If \(k \neq 0\), then \(x = a/k\)
Alternatively, if we need general solution of these DE \(x(t) = Ce^{kt} + a/k\), where \(e^{kt} \neq 0\) for any \(t\), then \(C\) must be \(0\), so \(x(t) = a/k\) for all times \(t\)
22 Why a constant solution could be unstable?
22.1 Front
Why a constant solution could be unstable?
For example: \(x(t) = Ce^{kt} + a/k\)
Assuming \(a,k > 0\)
22.2 Back
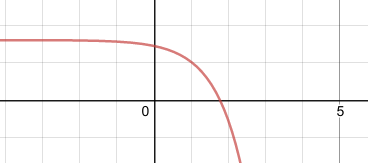
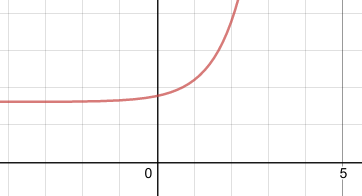
The constant solution is \(x = a/k\) (equilibrium point). Depends on initial values of \(x(0)\). If \(x(0)\) is above the equilibrium point then the population increases without bound. But if \(x(0)\) is below equilibrium then the population goes to zero.
If \(C lt 0\)
If \(C gt 0\)
If \(C = 0\)
23 Write this equation as \(y(x)\)
23.1 Front
Write this equation as \(y(x)\)
\({\displaystyle - \frac{1}{y-1} = - \frac{1}{x+1} + c}\)
23.2 Back
\(y = 1 + \frac{x+1}{1 - c(x+1)}\)
24 Model this DE
24.1 Front
Model this DE
The rate of change of a certain population is proportional to the square root of its size
24.2 Back
Let \(P = P(t)\) be the size of the population as a function of time \(t\)
\(\dv{P}{t} = k \sqrt{P}\)
where \(k>0\) is the constant of proportionality