1 Chalkboard
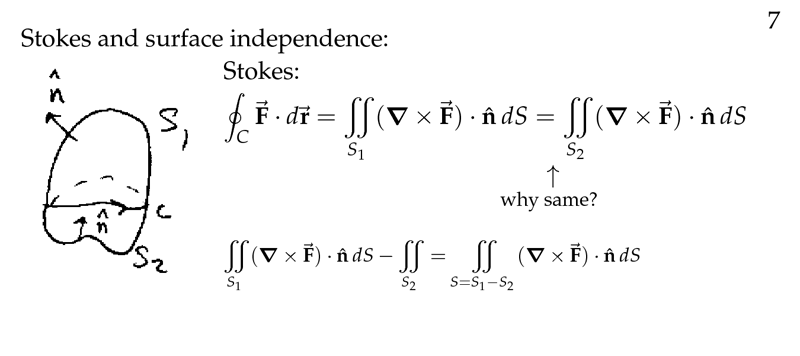
Figure 1: Stokes and surface independence
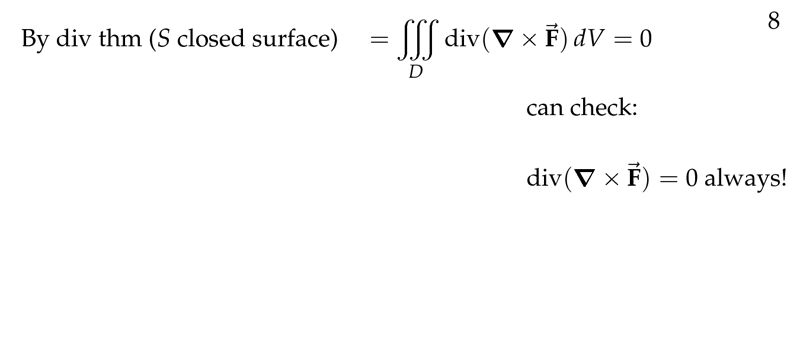
Figure 2: Check with divergence theorem
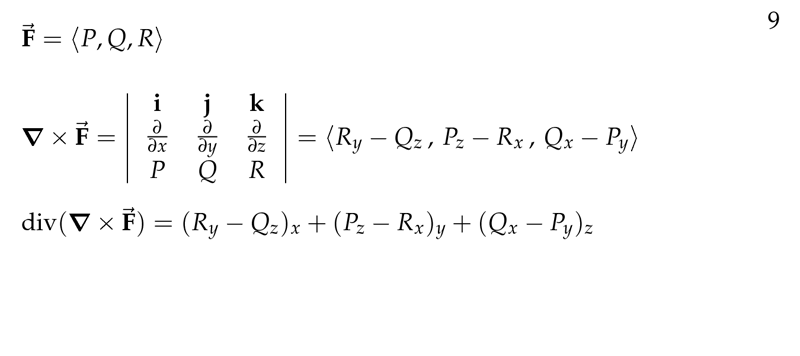
Figure 3: Divergence of curl of vector fiels is 0
Figure 4: For real vectors
2 Why for Stokes’ Theorem we can use any surface (surface independence)?
2.1 Front
Why for Stokes’ Theorem we can use any surface (surface independence)?
Let \(\vb{F}\) be a vector field defined for all space, \(C\) a closed curve
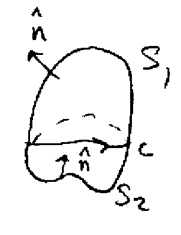
Why?
\({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = \iint_{S_1} (\curl{\vb{F}}) \cdot \vu{n} \dd{S} = \iint_{S_2} (\curl{\vb{F}})\cdot \vu{n} \dd{S}}\)
2.2 Back
I can get a closed surface with contains \(S_1\) and \(S_2\), which its normal vector is outwards the surface.
\({\displaystyle \iint_{S=S_1-S_2} (\curl{\vb{F}}) \cdot \vu{n} \dd{S} = \iint_{S_1} (\curl{\vb{F}}) \cdot \vu{n} \dd{S} - \iint_{S_2} (\curl{\vb{F}}) \cdot \vu{n} \dd{S}}\)
By the diverges theorem, Let \(D\) the interior region of the closed surface \(S\)
\({\displaystyle \iint_S (\curl{\vb{F}}) \cdot \vu{n} \dd{S} = \iiint_D \text{div} (\curl{\vb{F}}) \dd{V} = 0}\)
(Always \(\div{\curl{\vb{F}}} = 0\))
So, \({\displaystyle \iint_{S_1} (\curl{\vb{F}}) \cdot \vu{n} \dd{S} = \iint_{S_2} (\curl{\vb{F}})\cdot \vu{n} \dd{S}}\)
3 Which is the equation of the ellipse produced by…
3.1 Front
Which is the equation of the ellipse produced by…
- Plane: \(x+y+z=1\)
- Cylinder: \(x^2 + y^2 = 1\)
3.2 Back
Surface \(z = 1 -x -y\)
Parametrize the ellipse:
- \(x = \cos t\)
- \(y = \sin t\)
- \(z = 1 - \cos t - \sin t\)