1 Chalkboard

Figure 1: Stokes and Path Independence
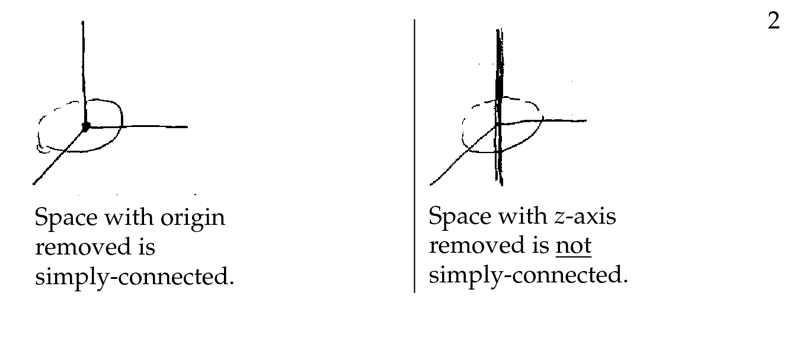
Figure 2: Examples of simply-connected spaces

Figure 3: Theorem for path independence of line integrals
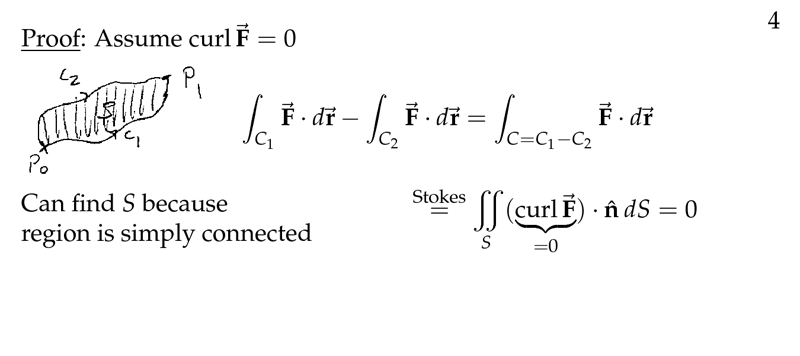
Figure 4: Proof of path independence of line integrals of conservative \(\vb{F}\)
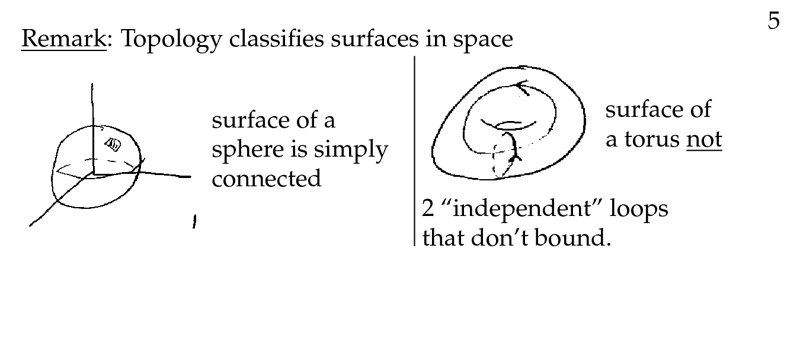
Figure 5: Topology examples

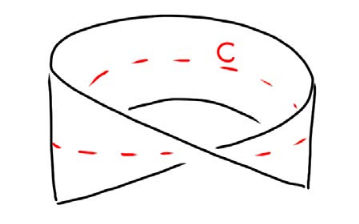
Figure 6: Non-orientable surface (Torus surfaces)
2 What does mean that a surface has only one side?
2.1 Front
What does mean that a surface has only one side?
2.2 Back
If you start painting them, you can use only one colour, if you don’t allow abrupt colour changes
This surface cannot be oriented, there is no continuous choice for the normal vector \(\vu{n}\) over this surface
It makes no sense to speak of “the flux through \(S\)”, because there is no consistent way of deciding on the positive direction for flow through the surface
Stokes’ theorem does not apply to such surfaces
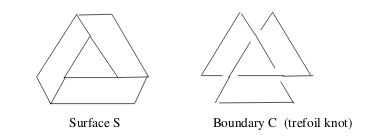
3 Can we find a two side surface which is boundary by \(C\)?
3.1 Front
Can we find a two side surface which is boundary by $C$?
Let \(D\) be a simply-connected region
3.2 Back
Yes, see 1930 van Kampen proof
Triangulation (this is simplification):
4 What does mean that domain \(D\) is simply-connected?
4.1 Front
What does mean that domain $D$ is simply-connected?
Domain \(D\) in 3-space
4.2 Back
Each closed curve in it can be shrunk to a point without ever getting outside of \(D\) during the shrinking
Example: 3-space, interior or exterior of a sphere
Non-example: Interior of a torus (a bagel, for instance) is not simply-connected
If \(D\) is simply-connected, then any closed curve \(C\) is the boundary of a two-sided surface (which may cross itself) lying entirely inside \(D\)
5 What can we say if \(D\) is simply-connected and \(\vb{F}\) is conservative?
5.1 Front
What can we say if $D$ is simply-connected and $\vb{F}$ is conservative?
Let \(\vb{F}\) be a conservative vector field continuously differentiable in \(D\), and \(C\) a closed curve
Explain why it’s possible, and consequences that \(\vb{F}\) is conservative
5.2 Back
Since \(D\) is simply-connected, given such a curve \(C\), we can find a two-sided surface \(S\) lying entirely in \(D\) and having \(C\) as its boundary.
Applying Stokes’ theorem
\({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{R}} = \iint_S \curl{\vb{F}} \cdot \dd{\vb{S}} = 0}\)
- \(\vb{F} = \grad{f}\)
- \(\text{curl}\vb{F} = 0\)
- \(\curl{\vb{F}} = 0\)
- \({\displaystyle \int_P^Q \vb{F} \cdot \dd{\vb{r}}}\) is path independence
- \({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = 0}\)
- Can use FTC for line integrals
6 Can we apply Stokes’ Theorem to this curve?
6.1 Front
Can we apply Stokes’ Theorem to this curve?
Let \(D\) be the exterior of the cylinder \(x^2 + y^2 = 1\), and \(C\) a circle around the outside of this cylinder
6.2 Back
No, because you cannot find any two-side surface lying inside \(D\) which boundary is the circle \(C\)
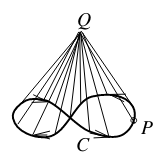
7 Is the 3-space with origin removed a simply-connected region?
7.1 Front
Is the 3-space with origin removed a simply-connected region?
7.2 Back
Yes, it is. You can move and shrink the curve to one point

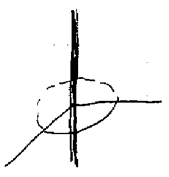
8 Is the 3-space with \(z\text{-axis}\) removed a simply-connected region?
8.1 Front
Is the 3-space with $z\text{-axis}$ removed a simply-connected region?
8.2 Back
No, it is not
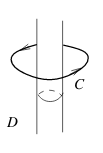
9 Is the 3-space with a circle removed a simply-connected region?
9.1 Front
Is the 3-space with a circle removed a simply-connected region?
9.2 Back
No, it’s not
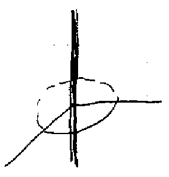
10 Is the 2-space with line segment removed a simply-connected region?
10.1 Front
Is the 2-space with line segment removed a simply-connected region?
10.2 Back
No, it is not. You cannot shrink the curve without touch the line segment. You cannot move it for shrink
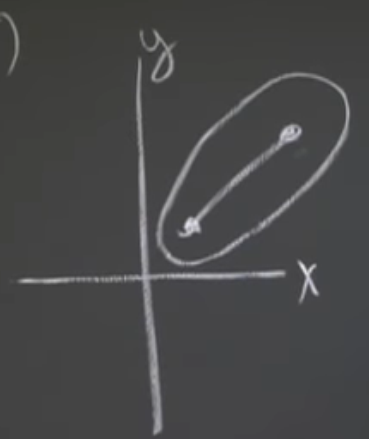
But, in 3D it’s simply connected
11 Is the solid torus a simply-connected region?
11.1 Front
Is the solid torus a simply-connected region?
11.2 Back
Not, it is not
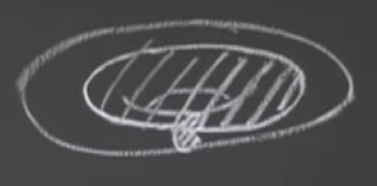
12 Is the surface of a torus a simply-connected region?
12.1 Front
Is the surface of a torus a simply-connected region?
12.2 Back
No, it is not. There are 2 “independent” loops that don’t bound

13 Is the paraboloid a simply-connected surface?
13.1 Front
Is the paraboloid a simply-connected surface?
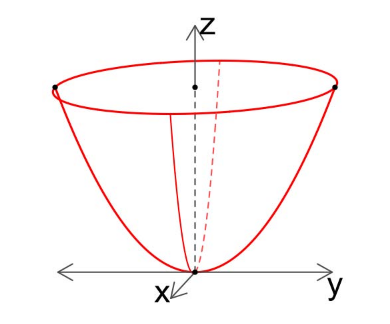
Paraboloid, \(z = x^2 + y^2\)
13.2 Back
Yes, any closed curve \(C\) on the surface of the paraboloid can be shrunk to a point
14 Is the Mobius strip a simply-connected surface?
14.1 Front
Is the Mobius strip a simply-connected surface?
14.2 Back
No. Think of the Mobius strip as a long, thin rectangle whose ends have been joined to make a loop. A closed curve \(C\) around that loop cannot be shrunk to a point without “getting outside of” the Mobius strip.