1 Chalkboard
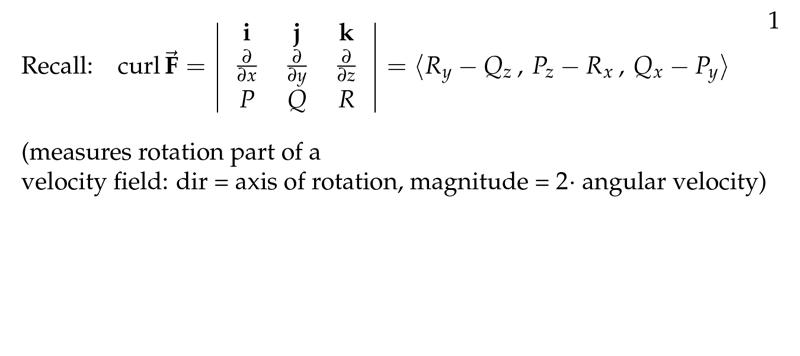
Figure 1: Recall \(\text{curl}\vb{F}\)
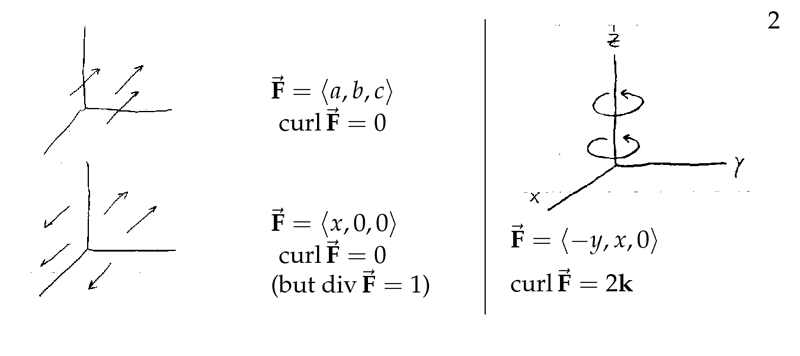
Figure 2: Curl examples

Figure 3: Stokes’ Theorem

Figure 4: Orientation of \(S\) and \(C\)

Figure 5: Right-hand rule for \(S\) and \(C\) orientation
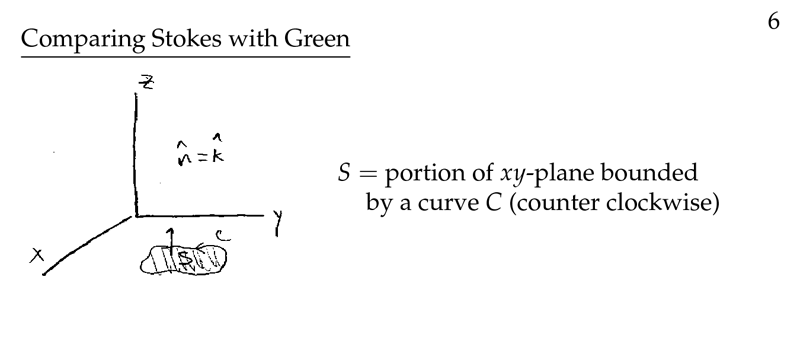
Figure 6: Comparing Stokes with Green
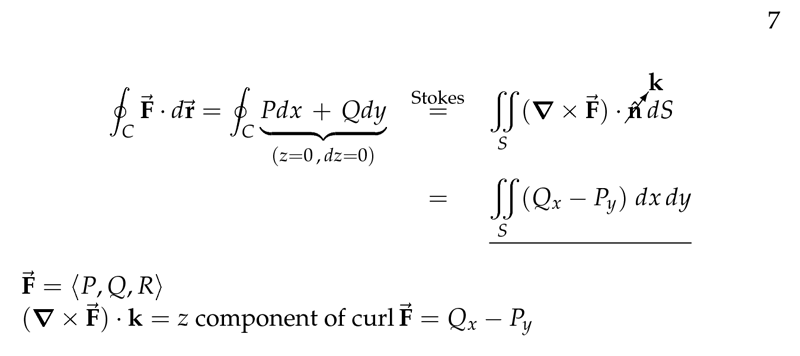
Figure 7: Green’s Theorem as special case of Stokes’ Theorem

Figure 8: Why stokes is true?
2 What is the Stokes’ Theorem
2.1 Front
What is the Stokes’ Theorem
Write it’s equation, and define its hypothesis, Let \(C\) be a curve and \(\vb{F}\) a vector field
2.2 Back
- \(C\) should be a closed curve
- \(S\) could be any surface which boundary is \(C\)
- Right-hand rule orientation
- \(\vb{F}\) must be defined in all \(S\)
\({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = \iint_S \curl{\vb{F}} \dd{\vb{S}}}\)
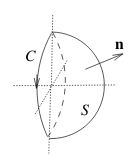
3 What does mean that \(C\) and \(S\) in Stokes’ Theorem should be compatibly oriented?
3.1 Front
What does mean that $C$ and $S$ in Stokes’ Theorem should be compatibly oriented?
3.2 Back
Using the right-hand rule, when you walk in the positive direction on \(C\), keeping \(S\) to your left, then your head should point in the direction of \(\vb{n}\)

4 How should be oriented these surfaces for Stokes’ Theorem
4.1 Front
How should be oriented these surfaces for Stokes’ Theorem

4.2 Back

5 Which is the normal vector of \(S\) for using Stokes’ Theorem?
5.1 Front
Which is the normal vector of $S$ for using Stokes’ Theorem?
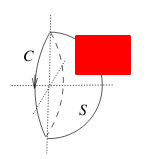
The surface is a half-sphere with radius \(1\)
5.2 Back
\(\vu{n} = \ev{x,y,z}\)
6 What is the relationship between Stokes’ theorem and Green Theorem
6.1 Front
What is the relationship between Stokes’ theorem and Green Theorem
Let \(\vb{F}\) be a vector field in space, and \(C\) a closed curve
6.2 Back
\(\vb{F} = \ev{M,N,P}\), and \(C\) a simple closed curve in the \(xy\text{-plane}\), oriented positively (so the interior is on your left as you walk upright in the positive direction)
Let \(S\) be the interior, compatibly oriented, \(\vu{n} = \vu{k}\), and \(\dd{S} = \dd{A}\)
\({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = \oint_C M \dd{x} + N \dd{y} = \iint_S \curl{\vb{F}} \cdot \vu{n} \dd{S} = \iint_R (N_x - M_y) \dd{A}}\) (which is the Greens’ Theorem)
This is true for other choices of the 2 variables
7 Which is the angular velocity of the paddle wheel in a 3D fluid flow?
7.1 Front
Which is the angular velocity of the paddle wheel in a 3D fluid flow?
Let \(\vb{F}\) be the velocity field for a 3D fluid flow, \(a\) be the radius of the paddle wheel, and \(P_0\) be the center of the paddle wheel
7.2 Back
Which is the angular velocity of the paddle wheel in a 3D fluid flow?
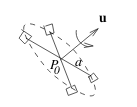
Angular velocity of the paddle wheel
\({\displaystyle \frac{1}{2 \pi a^2} \oint_C \vb{F} \cdot \dd{\vb{r}}}\)
By Stokes’ Theorem, \(S\) being the circular dist having \(C\) as boundary
\({\displaystyle \frac{1}{2 \pi a^2} \iint_S \curl{\vb{F}} \cdot \vu{u} \dd{S}}\)
Since \(\text{curl} \vb{F} \cdot \vu{u}\) is approximately constant on \(S\) if \(a\) is small and \(S\) has area \(\pi a^2\)
\({\displaystyle \approx \frac{1}{2 \pi a^2} (\text{curl} \vb{F})_0 \cdot \vu{u} (\pi a^2)}\)
As \(a \to 0\)
angular velocity of the paddle wheel \({\displaystyle = \frac{1}{2} \curl{\vb{F}} \cdot \vu{u}}\)
8 Which is the direction where the paddle wheel spin faster?
8.1 Front
Which is the direction where the paddle wheel spin faster?
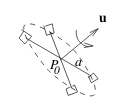
Let \(\vb{F}\) be the velocity vector field for a 3D fluid flow
8.2 Back
angular velocity of paddle wheel is \(\frac{1}{2} (\text{curl}\vb{F})_0 \cdot \vu{u}\)
Maximum value when \(\vu{u}\) has the direction of \((\text{curl}\vb{F})_0\)
- direction of \((\text{curl}\vb{F})_0\) axial direction in which wheel spins faster
- magnitude of \((\text{curl}\vb{F})_0\) is twice this maximum angular velocity