1 Chalkboard
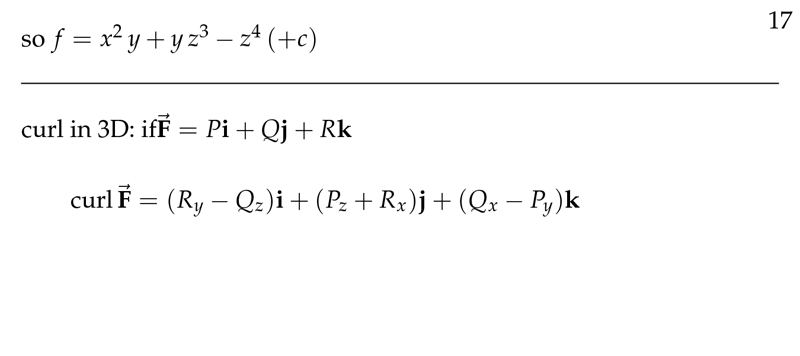
Figure 1: Curl in 3D
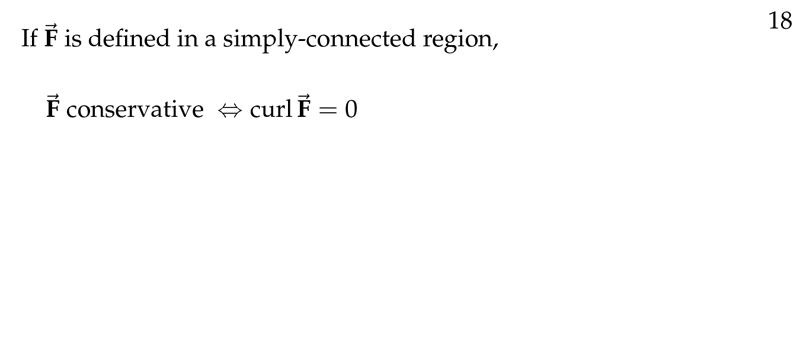
Figure 2: \(\vb{F}\) in simply-connected region

Figure 3: Del notation
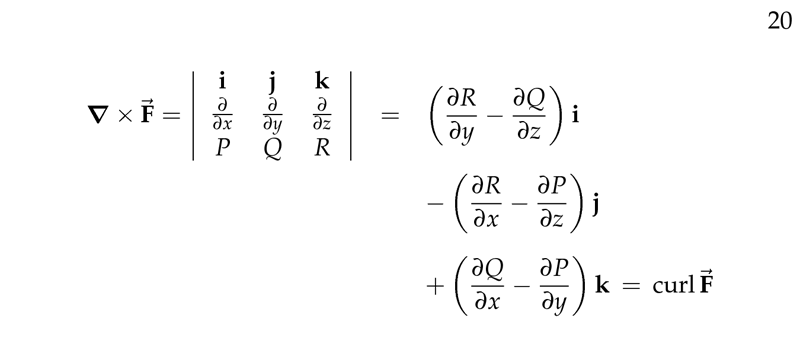
Figure 4: Mnemotecnic formula for curl \(\vb{F}\)
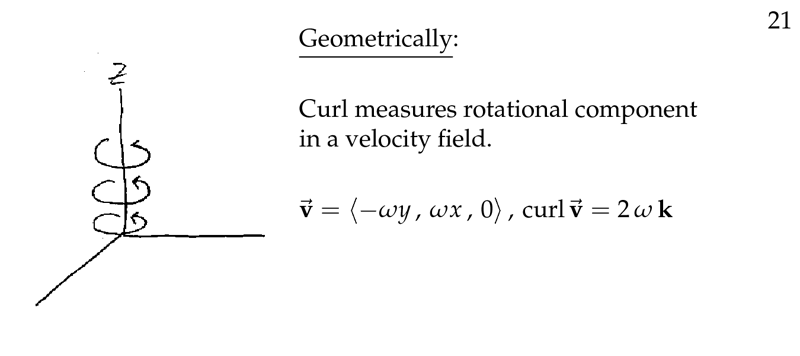
Figure 5: Geometric meaning of curl
2 Is the \(\text{curl}\vb{F}\) a scalar function?
2.1 Front
Is the $\text{curl}\vb{F}$ a scalar function?
Let \(\vb{F} = \ev{M,N}\) be a planar vector field
2.2 Back
In this case you can call it a scalar function because it only has \(\vu{k}\) component.
But really, curl is a vector function and in this case
\(\text{curl} \vb{F} = (N_x - M_y) \vu{k}\)
3 Write divergence theorem using del notation
3.1 Front
Write divergence theorem using del notation
Let \(\vb{F} = \ev{M,N,P}\) be a vector field
3.2 Back
\({\displaystyle \iint_S \vb{F} \cdot \dd{\vb{S}} = \iiint_D \div{\vb{F}} \dd{V}}\)
4 Compute this equation
4.1 Front
Compute this equation
\(\curl{\grad{f}}\)
4.2 Back
\(\curl{\grad{f}} = 0\), it was part of the criterion for gradient field
5 Compute this equation
5.1 Front
Compute this equation
\(\div{\curl{\vb{F}}}\)
5.2 Back
\(\div{\curl{\vb{F}}} = 0\)
Let \(\vb{F} = \ev{P,Q,R}\)
\({\displaystyle \curl{\vb{F}} = \ev{R_y - Q_z, P_z - R_x, Q_x - P_y}}\)
\({\displaystyle \div{\curl{\vb{F}}} = (R_y - Q_z)_x + (P_z - R_x)_y + (Q_x - P_y)_z = R_{yx} - Q_{zx} + P_{zy} - R_{xy} + Q_{xz} - P_{yz} = 0}\)
Note that for real vectors \(\vb{u} \cdot (\vb{u} \cross \vb{v}) = 0\)
6 How rapidly the flow spins the wheel?
6.1 Front
How rapidly the flow spins the wheel?
Let \(\vb{F}\) be a flow where \(\vb{v}\) is its velocity field. And there is a paddle wheel of radius \(a\) so its center is at \((x_0, y_0)\)
6.2 Back
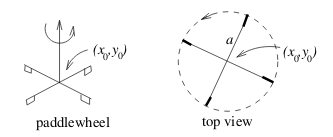
The velocity at one blade would be \(\vb{F}\cdot \vu{T}\), the component of the flow velocity vector \(\vb{F}\) perpendicular to the blade (Tangent to the circle of radius \(a\))
If we only have one blade the wheel would spin around at an uneven rate. If the wheel has many blades, this unevenness will be averaged out, and it will spin around at approximately the average value of the tangential velocity \(\vb{F} \cdot \vu{T}\)
So, this is the average tangential velocity of \(\vb{F} \cdot \vu{T}\) over the circle. Speed of blade:
\({\displaystyle \frac{1}{2 \pi a} \oint_C \vb{F} \cdot \vu{T} \dd{s} = \frac{1}{2\pi a} \oint_C \vb{F} \cdot \dd{\vb{r}}}\)
Applying Green’s Theorem
\({\displaystyle \frac{1}{2 \pi a} \iint_R \curl{\vb{F}}_0 \dd{x} \dd{y} \approx \frac{1}{2\pi a} (\curl{\vb{F}})_0 \pi a^2}\)
Where \((\curl{\vb{F}})_0\) is the value of the function curl \(\vb{F}\) at \((x_0,y_0)\). If the paddle wheel is small we can approximate the curl \(\vb{F}\) to \((\curl{\vb{F}})_0\) over the interior \(R\) of the circle
So we can deduce that \({\displaystyle \text{tangential speed} \approx \frac{a}{2} (\curl{\vb{F}})_0}\), getting rid \(a\), \({\displaystyle w_0 \approx \frac{1}{2} (\curl{\vb{F}})_0}\)
7 What measures the curl of \(\vb{F}\)?
7.1 Front
What measures the curl of $\vb{F}$?
Let \(\vb{F}\) be a flow
7.2 Back
It’s measures the “vorticity” of the fluid flow - its tendency to produce rotation
8 Get a formula for getting potential function by path method
8.1 Front
Get a formula for getting potential function by path method
Let \(\vb{F} = \ev{M,N,P}\)
8.2 Back
\(\vb{F} \cdot \dd{\vb{r}} = M \dd{x} + N \dd{y} + P \dd{z}\)
\({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}} = f(P_1) - f(P_0)}\), setting \(P_0 = (0,0,0)\) and \(P_1 = (x_1, y_1, z_1)\)
Draw a path with 3 path from \((0,0,0)\) to \((x_1,0,0)\) to \((x_1, y_1, 0)\) to \((x_1, y_1, z_1)\)
\({\displaystyle f(x_1, y_1,z_1) = \int_0^{x_1} M(x,0,0) \dd{x} + \int_0^{y_1} N(x_1, y, 0) \dd{y} + \int_0^{z_1} P(x_1,y_1,z) \dd{z}}\)