1 Chalkboard
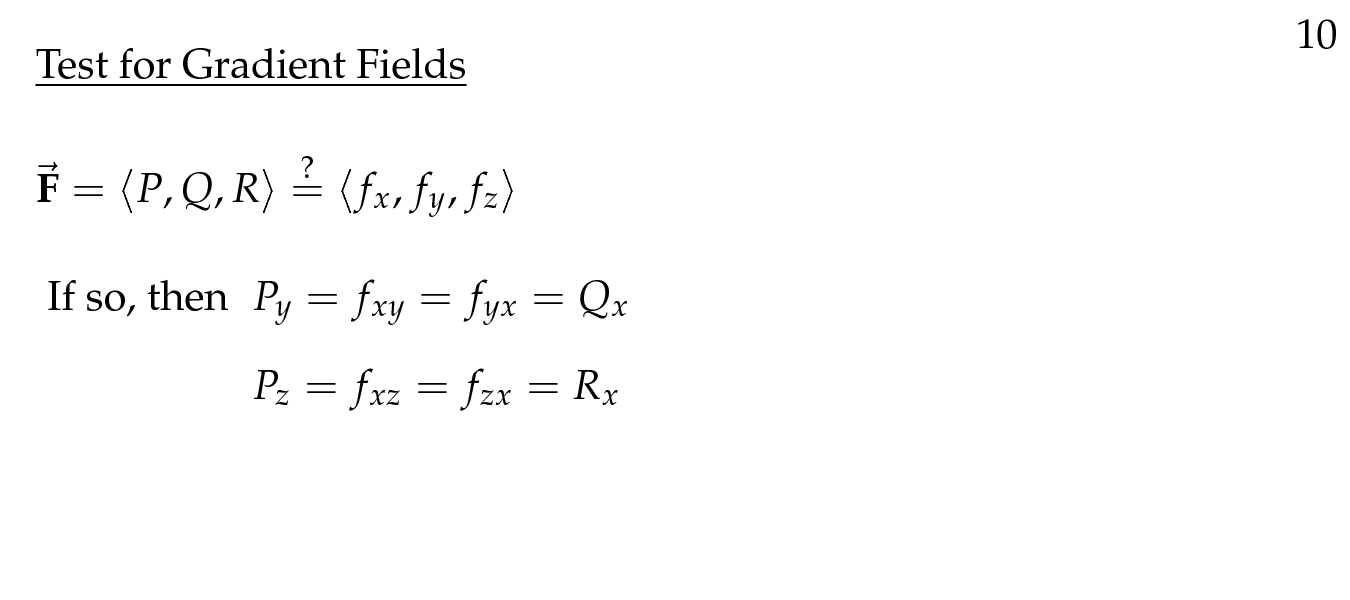
Figure 1: Test for Gradient Fields

Figure 2: Criterion for Gradient Field
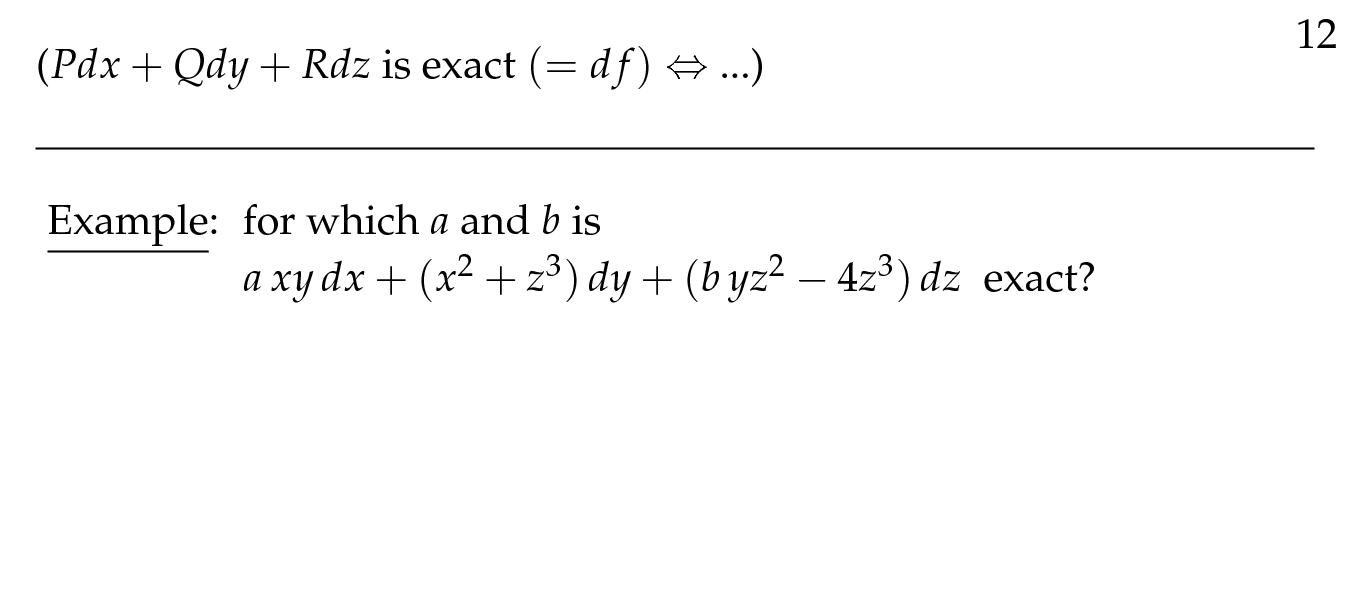
Figure 3: Example for criterion gradient field
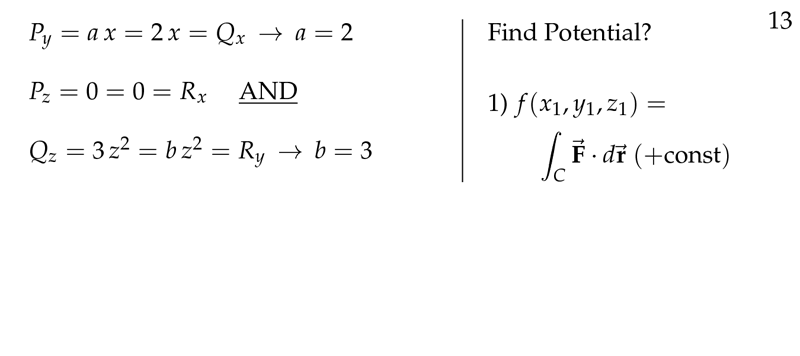
Figure 4: Find the Potential
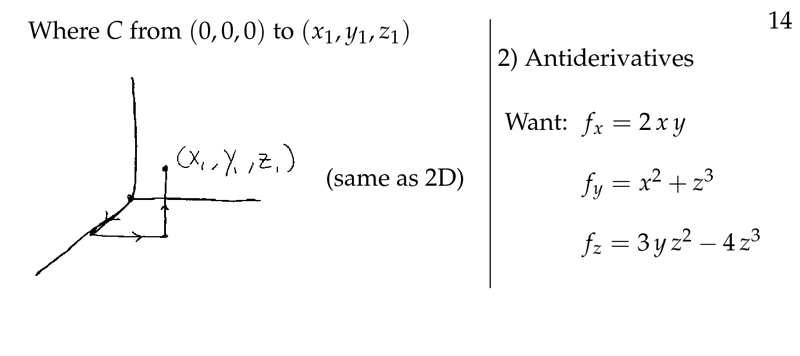
Figure 5: FTC and Path method
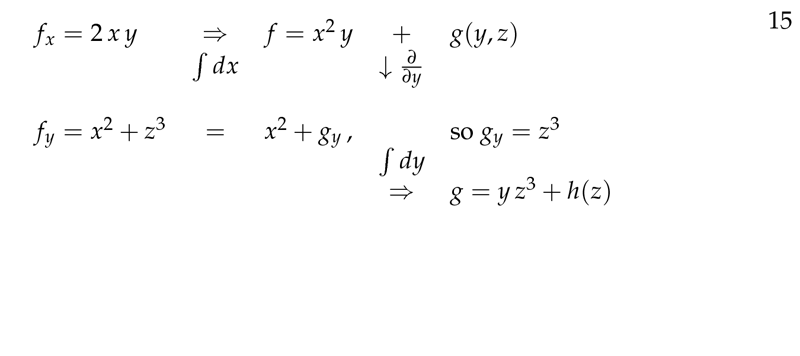
Figure 6: Antiderivative method
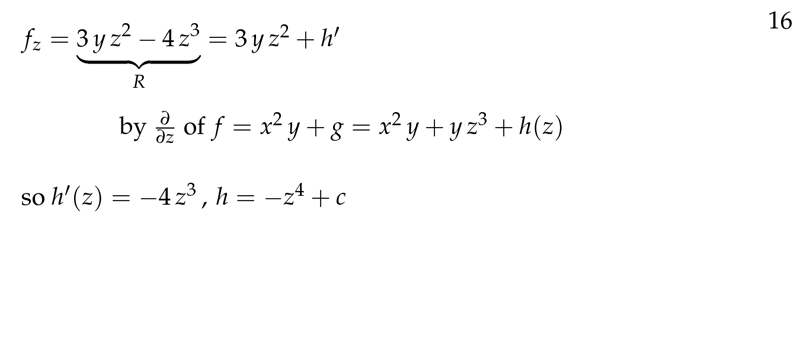
Figure 7: Antiderivative method II
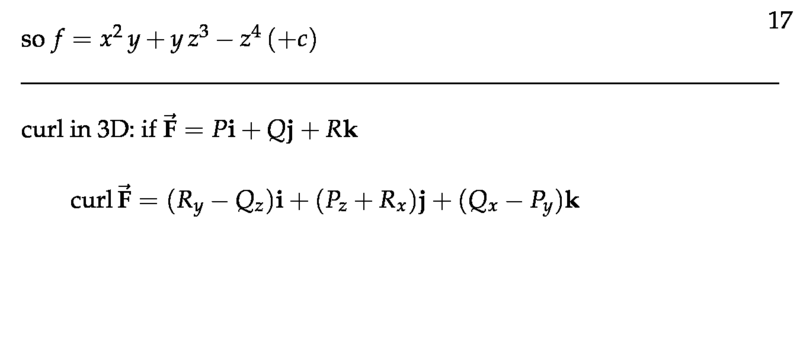
Figure 8: Antiderivative result
2 How is the Criterion for a gradient field in space?
2.1 Front
How is the Criterion for a gradient field in space?
Let \(\vb{F} = M \vu{i} + N \vu{j} + P \vu{k}\)
2.2 Back
\(\vb{F}\) must be continuously differentiable for the region
- \(M_y = N_x\)
- \(M_z = P_x\)
- \(N_z = P_y\)
3 Why the Criterion is valid for testing \(\vb{F}\) is a gradient field?
3.1 Front
Why the Criterion is valid for testing $\vb{F}$ is a gradient field?
Let \(\vb{F} = \ev{M,N,P}\)
3.2 Back
\(\vb{F}\) is continuously differentiable
If \(\vb{F} = \grad{f}\), then \({\displaystyle \pdv{M}{y} = \pdv{f}{y}{x} = \pdv{f}{x}{y} = \pdv{N}{x}}\)
The two mixed partial derivatives are equals since they are continuous, by the hypothesis that \(\vb{F}\) is continuously differentiable
4 How are defined the \(\text{curl}\vb{F}\) in space?
4.1 Front
How are defined the $\text{curl}\vb{F}$ in space?
Let \(\vb{F} = \ev{M,N,P}\)
4.2 Back
\(\vb{F}\) is continuously differentiable
\begin{align*} \text{curl} \vb{F} &= (P_y - N_z) \vu{i} + (M_z - P_x) \vu{j} + (N_x - M_y) \vu{k} \\\ &= \begin{vmatrix}\vu{i} & \vu{j} & \vu{k} \ \pdv{x} & \pdv{y} & \pdv{z} \ M & N & P \end{vmatrix}\\\ &= \curl{F} \end{align*}
5 Which is the Criterion for exact differentials?
5.1 Front
Which is the Criterion for exact differentials?
Check that \(\dd{f} = M \dd{x} + N \dd{y} + P \dd{z}\) is exact
5.2 Back
Let \(D\) be a domain in which \(M,N,P\) are continuously differentiable. In \(D\)
\(M \dd{x} + N \dd{y} + P \dd{z}\) is exact \(\Leftrightarrow P_y = N_z, M_z = P_x, N_x = M_y\)
6 Are the method for getting potential function valid for 3 dimension?
6.1 Front
Are the method for getting potential function valid for 3 dimension?
6.2 Back
Both methods (FTC for Line Integrals, and Antiderivatives) are valid for getting potential function from \(\vb{F} = \grad{f}\).
You need to check, that \(\vb{F} = \ev{M,N,P}\) are continuously differentiable for all region, and use the Criterion for checking that \(\vb{F} = \grad{f}\)
7 Are all properties of conservative vector field valid for 3D?
7.1 Front
Are all properties of conservative vector field valid for 3D?
7.2 Back
Yes, you can use all properties of conservative vector field in space.
You need to check that the vector field is continuously differentiable for all the region where you’ll use it.