1 Chalkboard
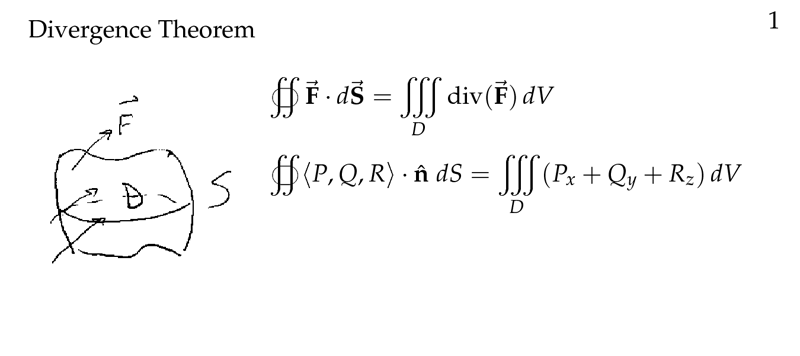
Figure 1: Recall divergence theorem

Figure 2: “Del” notation

Figure 3: Physical interpretation of divergence
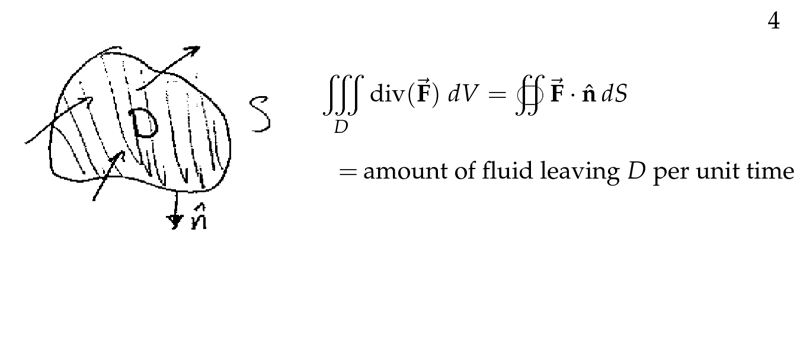
Figure 4: Amount of fluid leaving \(D\) per unit time
2 What means “source rate”?
2.1 Front
What means “source rate”?
\(\text{div} \vb{F}\) is “source rate”. Explain by words
2.2 Back
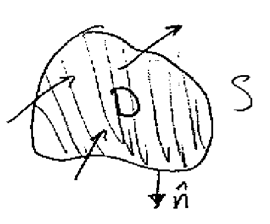
Amount of flux generated per unit volume. With Gauss-Green’s Theorem is the amount of fluid leaving \(D\) per unit time
3 Expand this equation
3.1 Front
Expand this equation
\({\displaystyle \grad{} \cross \vb{F}}\), Let \(\vb{F} = \ev{P,Q,R}\)
3.2 Back
\({\displaystyle \biggl(\pdv{R}{y} - \pdv{Q}{z} \biggr) \vu{i} + \biggl( \pdv{P}{z} - \pdv{R}{x} \biggr) \vu{j} + \biggl( \pdv{Q}{x} - \pdv{P}{y} \biggr) \vu{k}}\)
4 Expand this equation
4.1 Front
Expand this equation
\({\displaystyle \vb{F} \cdot \grad{}}\), Let \(\vb{F} = \ev{P,Q,R}\)
4.2 Back
\({\displaystyle P \pdv{}{x} + Q \pdv{}{y} + R \pdv{}{z}}\)
5 Expand this equation
5.1 Front
Expand this equation
\({\displaystyle \frac{1}{2} \grad{} (\vb{F} \cdot \vb{F})}\)
5.2 Back
\({\displaystyle \frac{1}{2} \grad{} (P^2 + Q^2 + R^2) = \biggl(P \pdv{P}{x} + Q \pdv{Q}{x} + R \pdv{R}{x} \biggr) \vu{i} + \biggl(P \pdv{P}{y} + Q \pdv{Q}{y} + R \pdv{R}{y} \biggr) \vu{j} + \biggl(P \pdv{P}{z} + Q \pdv{Q}{z} + R \pdv{R}{z} \biggr) \vu{k}}\)