1 Chalkboard
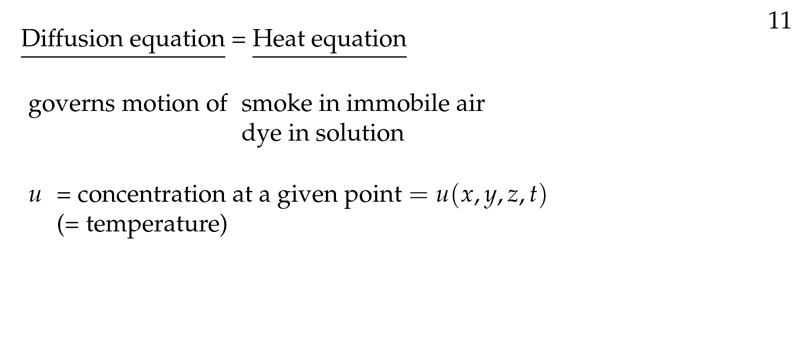
Figure 1: Introduction to Diffusion Equation

Figure 2: Heat equation
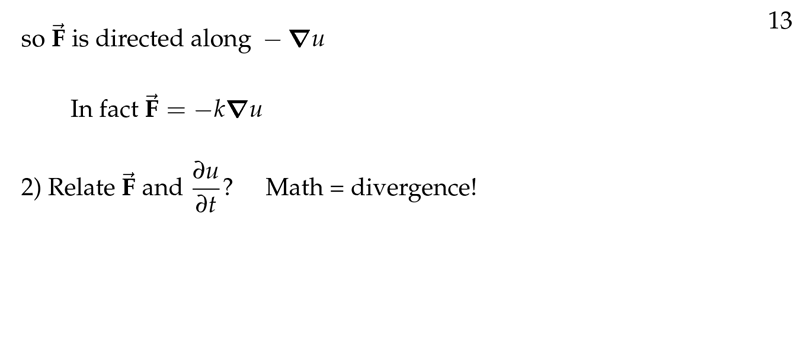
Figure 3: How relate \(\vb{F}\) with \(\pdv{u}{t}\)
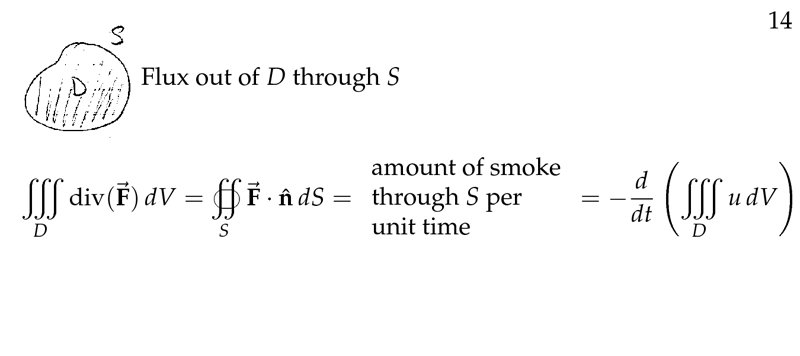
Figure 4: Using divergence theorem
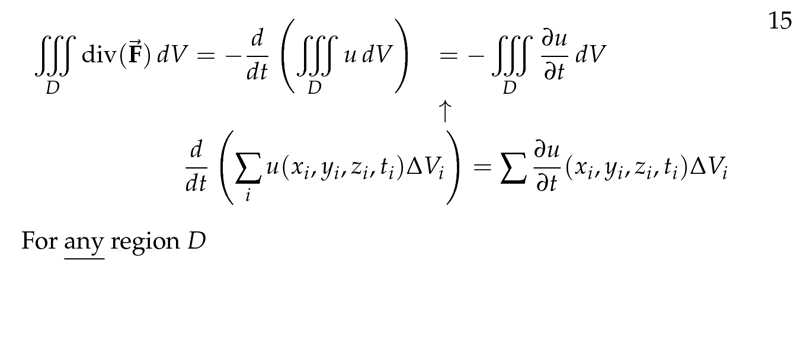
Figure 5: Setting equations for divergence equality
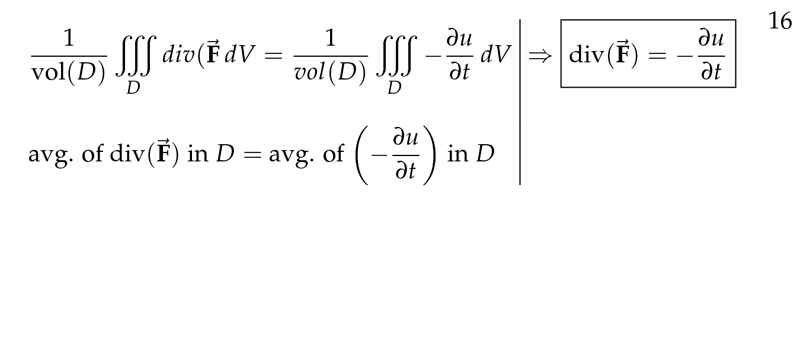
Figure 6: Divergence of flow
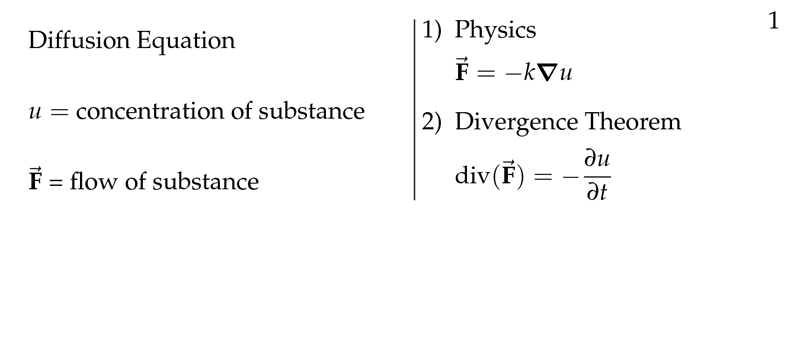
Figure 7: Diffusion Equation Recall

Figure 8: Result of Diffusion Equation
2 What is the Laplacian of function \(u(x,y,z)\)
2.1 Front
What is the Laplacian of function $u(x,y,z)$
2.2 Back
\(\laplacian{u} = \div{\grad{u}}\), is the \(\text{div}(\grad{u})\)
\(\laplacian{u} = \pdv[2]{u}{x} + \pdv[2]{u}{y} + \pdv[2]{u}{z}\)
3 What means that the function \(u(x,y,z)\) is harmonic?
3.1 Front
What means that the function $u(x,y,z)$ is harmonic?
3.2 Back
\(\laplacian{u} = \pdv[2]{u}{x} + \pdv[2]{u}{y} + \pdv[2]{u}{z} = 0\)
4 Differentiate \(A\) with respect to \(R\)
4.1 Front
Differentiate $A$ with respect to $R$
\({\displaystyle A = k \iint_S u(x,y,z) \dd{S}}\)
4.2 Back
\({\displaystyle \dv{A}{R} = \dv{k \iint_S u(x,y,z) \dd{S}}{R} = k \iint_S \dv{u(x,y,z)}{R} \dd{S} = k \iint_S \pdv{u}{x} \dv{x}{R} + \pdv{u}{y} \dv{y}{R} + \pdv{u}{z} \dv{z}{R} \dd{S}}\)
Using derivative sum rule for Riemman sum