1 Chalkboard

Figure 1: Proof of divergence theorem
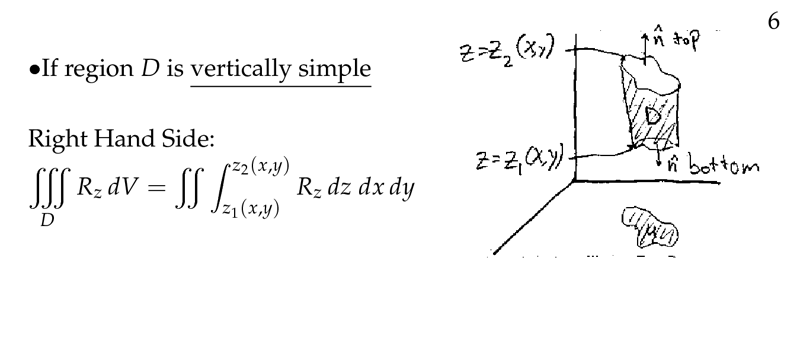
Figure 2: \(D\) is vertically simple

Figure 3: Checking both sides has same outcome
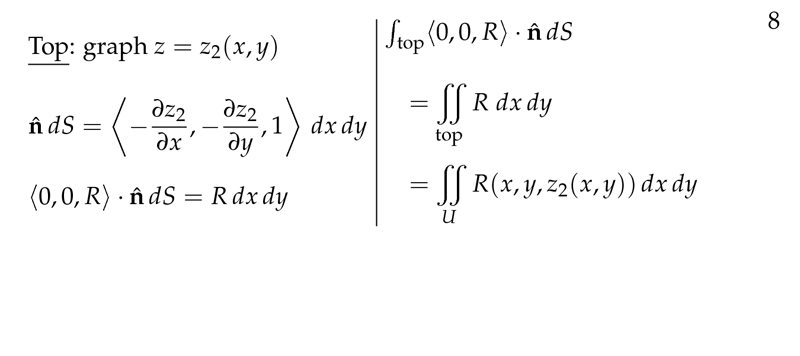
Figure 4: Flux at top side
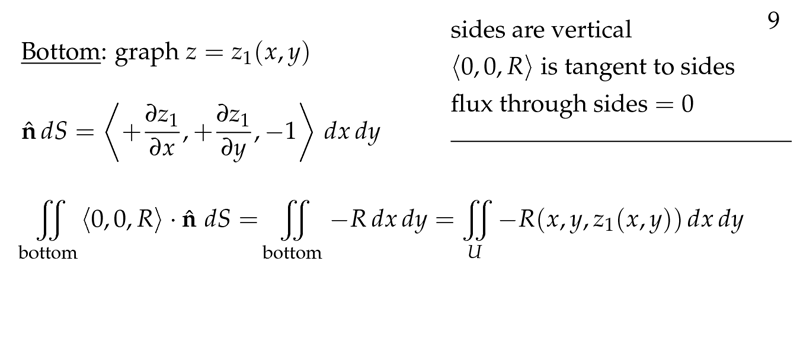
Figure 5: Flux at bottom side
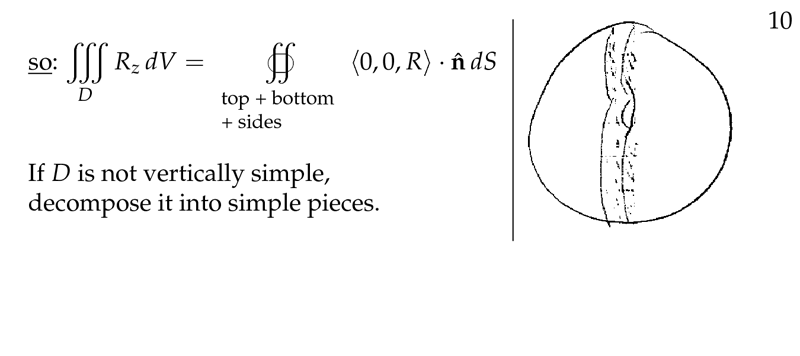
Figure 6: QED and divide up complex regions
2 How proof the divergence theorem
2.1 Front
How proof the divergence theorem
Describe only the steps
2.2 Back
- Let \(\vb{F}\) be a vector field with only 1 component
- You can proof separately and sum up then
- Divide up the figure in cubes, the flux at shared sides will be 0
- Set the Gauss theorem equation with this conditions
- Expand the equations side by side, and compare
3 Draw a figure for proofing the divergence theorem
3.1 Front
Draw a figure for proofing the divergence theorem
Let \(\vb{F} = \ev{0,0,P(x,y,z)}\)
3.2 Back
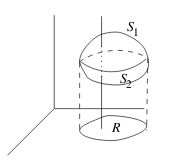
- \(S\) is a closed surface assuming vertically simple
- Lower surface: \(z = g(x,y)\)
- Upper surface: \(z = h(x,y)\)
4 Set up the divergence theorem equation for proofing it
4.1 Front
Set up the divergence theorem equation for proofing it
Let \(\vb{F} = \ev{0,0,P}\), \(S\) a closed surface vertically simple, where lower surface is \(z = g(x,y)\) and upper surface \(z = h(x,y)\)
And proof that has the same outcome
4.2 Back
\({\displaystyle \iint_S P \vu{k} \cdot \vu{n} \dd{S} = \iiint_D \pdv{P}{z} \dd{V}}\)
Right side:
\({\displaystyle \iiint_D \pdv{P}{z} \dd{V} = \iint_R \int_{g(x,y)}^{h(x,y)} \pdv{P}{z} \dd{z} \dd{x} \dd{y} = \iint_R (P(x,y,h) - P(x,y,g)) \dd{x} \dd{y}}\)
Left side:
- Calculating \(\dd{\vb{S}}\) for top and bottom side
- \(\dd{\vb{S}} = \pm \ev{-z_x, -z_y, 1} \dd{x} \dd{y}\)
- Positive is for top side
- Negative is for bottom side
- Flux at lateral sides is \(0\) because \(\vb{F} = \ev{0,0,P}\) and it’s perpendicular to \(\dd{\vb{S}}\) of lateral sides
- \(R\) is the region shadow in the \(xy\text{-plane}\)
- Top side
- \({\displaystyle \iint_{\text{top}} P \vu{k} \cdot \dd{\vb{S}} = \iint_R P(x,y,z)\dd{x}\dd{y} = \iint_R P(x,y,h(x,y)) \dd{x}\dd{y}}\)
- Bottom side
- \({\displaystyle \iint_{\text{bottom}} P \vu{k} \cdot \dd{\vb{S}} = \iint_R -P(x,y,z)\dd{x}\dd{y} = \iint_R P(x,y,g(x,y)) \dd{x}\dd{y}}\)
- Adding up all sides
- \({\displaystyle \iint_S P \vu{k} \cdot \dd{\vb{S}} = \iint_R P(x,y,h) \dd{x} \dd{y} - \iint_R P(x,y,g) \dd{x} \dd{y}}\)
5 Why can you divide up a region in smaller domain for proofing divergence theorem?
5.1 Front
Why can you divide up a region in smaller domain for proofing divergence theorem?
5.2 Back
You can divide up \(D\) into smaller domains \(D_i\) which are bounded by such surfaces \(S_i\). Adding these up gives the divergence theorem for \(D\) and \(S\), since the surface integrals over the new faces introduced by cutting up \(D\) each occur twice, with opposite normal vectors \(\vu{n}\), so that they cancel out.
After addition, one ends up just with the surface integral over the original \(S\)
Similar as Green’s Theorem for 2D