1 Chalkboard

Figure 1: Divergence theorem
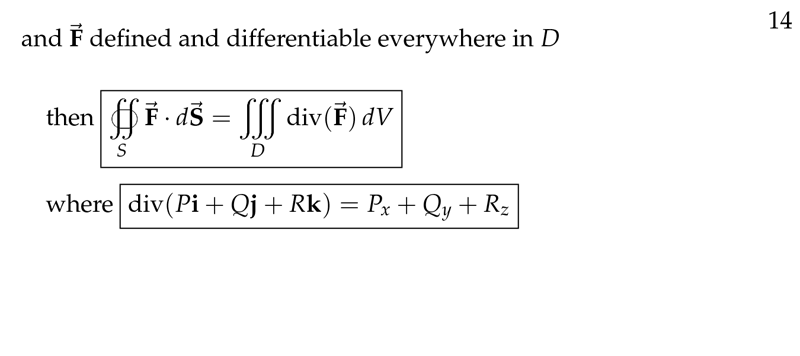
Figure 2: Equation of divergence theorem
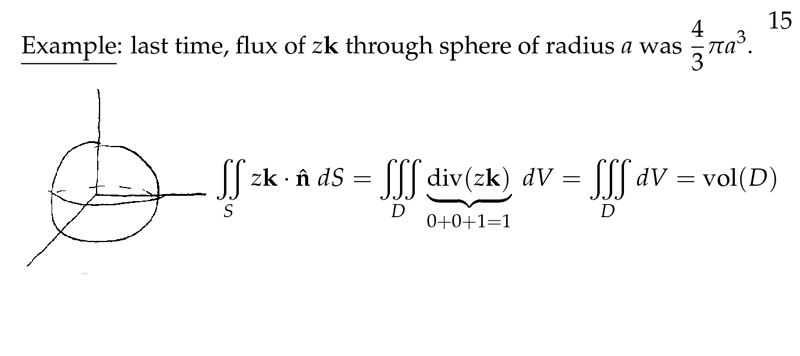
Figure 3: Example of divergence theorem
2 Which is the divergence of \(\vb{F}\)?
2.1 Front
Which is the divergence of $\vb{F}$?
Let \(\vb{F} = M \vu{i} + N \vu{j} + P \vu{k}\)
2.2 Back
\(\vb{F}\) is a vector field differentiable in some region \(D\), where we are calculating the divergence
\({\displaystyle \text{div} \vb{F} = \pdv{M}{x} + \pdv{N}{y} + \pdv{P}{z} = M_x + N_y + P_z}\)
3 Define physically what means the divergence theorem in 3 space?
3.1 Front
Define physically what means the divergence theorem in 3 space?
Or Gauss’ Theorem
Let \(\vb{F}\) a 3D flow field
3.2 Back
\({\displaystyle \oiint_S \vb{F} \cdot \dd{\vb{S}} = \iiint_D \text{div} \vb{F} \dd{V}}\)
- The surface integral: The mass transport rate across the closed surface \(S\), with flow out of \(S\) considered as positive, flow into \(S\) as negative
- The \(\text{div} F\) at \((x,y,z)\) is the source rate at \((x,y,z)\) is the rate at which fluid is being added to the flow at this point (positive). Negative rate means fluid is being removed from the flow. So the integral is the source rate for \(D\)
flux across \(S\) = source rate for \(D\)
The net flow outward across \(S\) is the same as the rate at which fluid is being produced (or added to the flow) inside \(S\)
4 How can we show that the flux across \(S\) is equals to source rate for \(D\)?
4.1 Front
How can we show that the flux across $S$ is equals to source rate for $D$?
Where \(S\) is a closed surface, and \(D\) is the interior region of \(S\)
Or show that \(\text{div} \vb{F}\) is the source rate at \((x,y,z)\)
Let \(\vb{F} = \ev{M,N,P}\)
4.2 Back
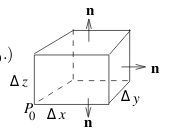
- \(\vb{n}\) always pointing outwards
- \(P_0 = (x_0, y_0, z_0)\) point inside the region \(D\) where \(\vb{F}\) is defined
- For top and bottom surface, we calculate the total flux across these surface
- Similar to front and back, and the 2 side faces
- Flux across top
- \(\vb{F}(x_0, y_0, z_0 + \Delta z) \cdot \vu{k} \Delta x \Delta y = P(x_0, y_0, z_0 + \Delta z) \Delta x \Delta y\)
- Flux across bottom
- \(\vb{F}(x_0, y_0, z_0) \cdot -\vu{k} \Delta x \Delta y = -P(x_0, y_0, z_0) \Delta x \Delta y\)
- Total flux (top + bottom)
- \([P(x_0, y_0, z_0 + \Delta z) - P(x_0, y_0, z_0)] \Delta x \Delta y = \biggl(\frac{\Delta P}{\Delta z} \biggr) \Delta x \Delta y \Delta z\)
- Net flux across pairs sides is approx
- \(\biggl(\pdv{P}{z} \biggr)_0 \Delta x \Delta y \Delta z\)
- \(\biggl(\pdv{N}{y} \biggr)_0 \Delta x \Delta y \Delta z\)
- \(\biggl(\pdv{M}{x} \biggr)_0 \Delta x \Delta y \Delta z\)
- Source rate for box is equals to net flux across the faces of box is
approx
- \(\biggl(\pdv{M}{x} + \pdv{N}{y} + \pdv{P}{z} \biggr)_0 \Delta x \Delta y \Delta z\)
So the interpretation for \(\text{div} \vb{F}\)
source rate at \(P_0\) = \({\displaystyle \lim_{\text{box} \to 0} \frac{\text{source rate for box}}{\text{volume of box}} = (\text{div} \vb{F})_{0} = \biggl(\pdv{P}{z} + \pdv{N}{y} + \pdv{P}{z} \biggr)_0}\)
5 What is the del notation?
5.1 Front
What is the del notation?
Expand their components
5.2 Back
\(\vb{\grad} = \ev{\pdv{}{x}, \pdv{}{y}, \pdv{}{z}}\)
6 What is the difference between these notations?
6.1 Front
What is the difference between these notations?
\(\grad{f}\) and \(\grad \cdot \vb{F}\)
6.2 Back
- \({\displaystyle \grad{f} = \ev{\pdv{f}{x}, \pdv{f}{y}, \pdv{f}{z}}}\) (gradient)
- \({\displaystyle \grad{} \cdot \vb{F} = \ev{\pdv{}{x}, \pdv{}{y}, \pdv{}{z}} \cdot \ev{P, Q, R} = \pdv{P}{x} + \pdv{Q}{y} + \pdv{R}{z}}\) (divergence)