1 Chalkboard
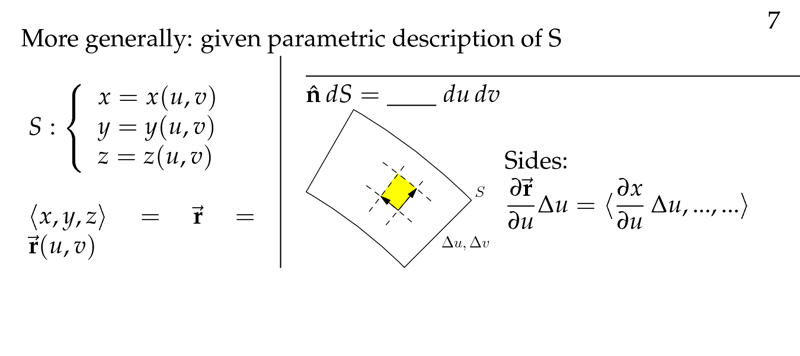
Figure 1: Generic description of \(S\)
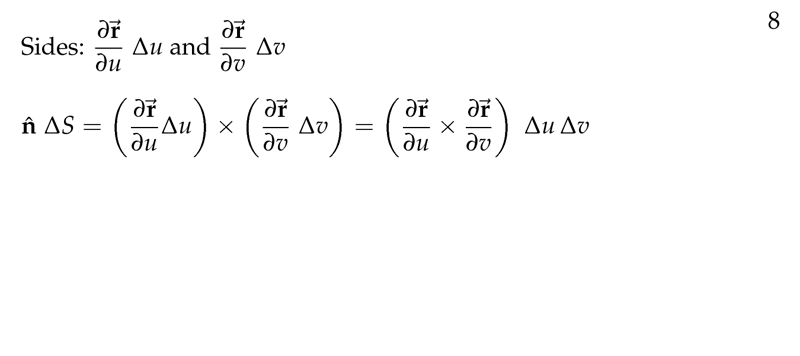
Figure 2: Sides of surface
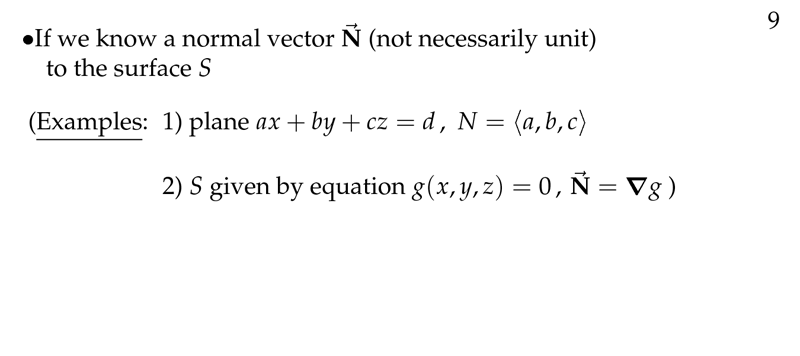
Figure 3: Knowing the normal vector of the surface
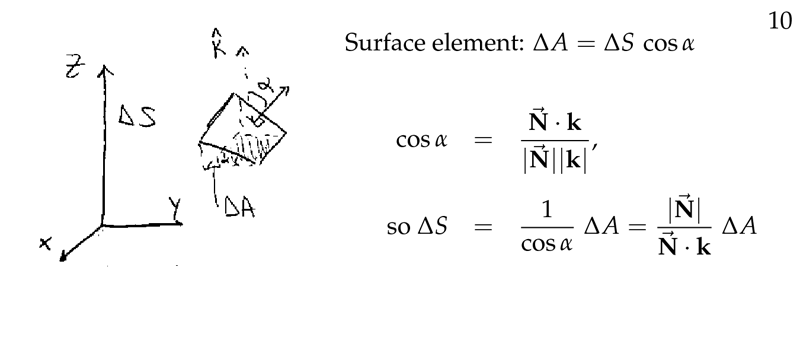
Figure 4: Surface element
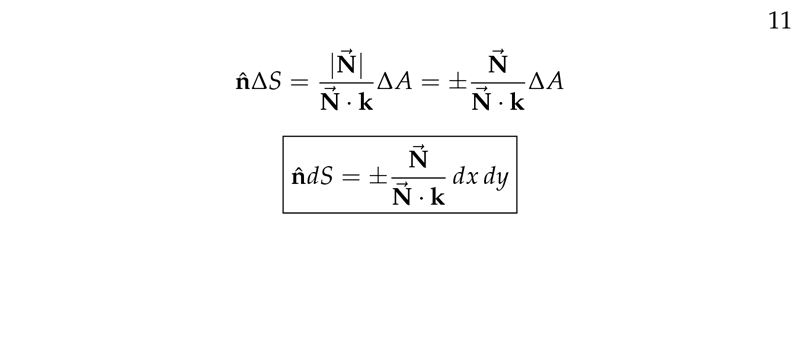
Figure 5: Writing \(\vu{n} \dd{S}\)
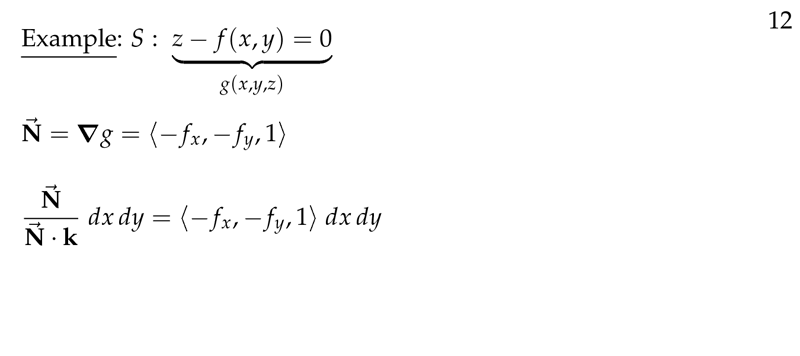
Figure 6: Example of generic surface
2 How can we get \(\dd{S}\) for any general surface?
2.1 Front
How can we get $\dd{S}$ for any general surface?
Where \(\dd{\vb{S}} = \vu{n} \dd{S}\)
2.2 Back
Since \(\dd{\vb{S}} = \vu{n} \dd{S}\), the area element \(\dd{S}\) is the magnitude of \(\dd{\vb{S}}\)
- \(z = z(x,y)\), \(\dd{\vb{S} = \ev{-z_x, -z_y, 1} \dd{x} \dd{y}}\), so \({\displaystyle \dd{S} = \sqrt{z_x^2 + z_y^2 + 1} \dd{x} \dd{y}}\)
- \(F(x,y,z) = c\), \({\displaystyle \dd{\vb{S}} = \frac{\grad{F}}{F_z} \dd{x} \dd{y}}\), so \({\displaystyle \dd{S} = \frac{\abs{\grad{F}}}{\abs{F_z}} \dd{x} \dd{y}}\)
3 Which is the general formula for \(\vu{n} \dd{S}\) knowing the normal vector?
3.1 Front
Which is the general formula for $\vu{n} \dd{S}$ knowing the normal vector?
Where, \(\vb{N}\) is the normal vector
3.2 Back
\({\displaystyle \vu{n} \dd{S} = \frac{\vb{N}}{\vb{N} \cdot \vu{k}} \dd{x} \dd{y}}\)
If \(\vb{N} = \grad{g}(x,y,z)\), then
\({\displaystyle \vu{n} \dd{S} = \frac{\grad{g}}{\grad{g} \cdot \vu{k}} \dd{x} \dd{y} = \frac{\grad{g}}{G_z} \dd{x} \dd{y}}\)
4 Which is the normal vector of the surface \(g(x,y,z) = c\)?
4.1 Front
Which is the normal vector of the surface $g(x,y,z) = c$?
4.2 Back
\(\vb{N} = \grad{g}\)
5 How is the outward normal of the paraboloid?
5.1 Front
How is the outward normal of the paraboloid?
Where the paraboloid is described by \(z = x^2 + y^2\). Get the vector \(\vu{n} \dd{S}\)
5.2 Back
The outward normal \(\vb{n}\) points away from the outside of the bowl and downward, then the component of \(\vb{n}\) is negative, so
\(\vu{n} \dd{S} = \ev{z_x, z_y, -1} \dd{x} \dd{y} = \ev{2x, 2y, -1} \dd{x} \dd{y}\)
6 What is a closed surface?
6.1 Front
What is a closed surface?
6.2 Back
Is a surface consisting of one connected piece which doesn’t intersect itself, and which completely encloses a single finite region \(D\) of space called it’s interior.
The closed surface \(S\) is then said to be the boundary of \(D\), we include \(S\) in \(D\)
Examples: Sphere, cube, torus,…
Non-closed surfaces: plane, sphere with one point removed, a tin can whose cross-section looks like a figure-8, infinite cylinder
7 How is the positive normal vector of a closed surface?
7.1 Front
How is the positive normal vector of a closed surface?
Normal vector: \(\vb{n}\)
7.2 Back
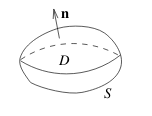
\(\vb{n}\) points away from the interior (points toward the outside)
8 How is the 3-space normal form of Green’s Theorem?
8.1 Front
How is the 3-space normal form of Green’s Theorem?
Let \(\vb{F}(x,y,z) = M \vu{i} + N \vu{j} + P \vu{k}\)
8.2 Back
- Let \(S\) be a positively-oriented closed surface with interior \(D\)
- \(\vb{F}\) is a vector field continuously differentiable in a domain containing \(D\)
- \({\displaystyle \text{div} \vb{F} = \pdv{M}{x} + \pdv{N}{y} + \pdv{P}{z} = M_x + N_y + P_z}\)
The divergence theorem (“Gauss-Green’s theorem”)
\({\displaystyle \oiint_{S} \vb{F} \cdot \dd{\vb{S}} = \iiint_D \text{div} \vb{F} \dd{V}}\)