1 Chalkboard

Figure 1: Flux of \(\vb{F}\) through surface \(S\)
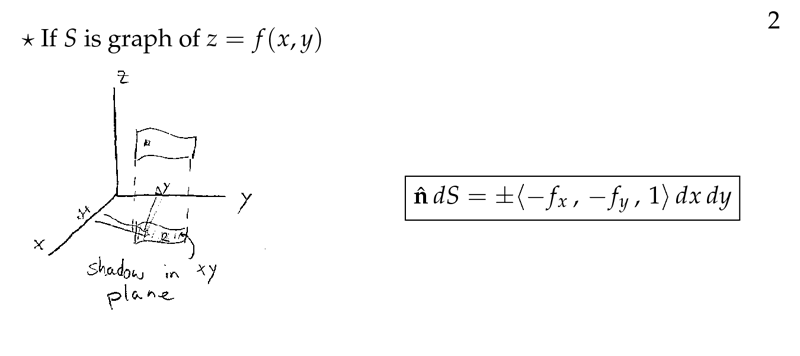
Figure 2: Normal unit vector and surface element
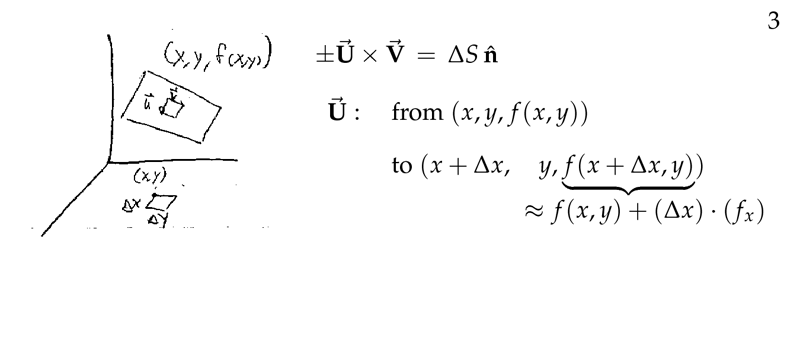
Figure 3: Getting \(\vu{n} \dd{S}\) - I
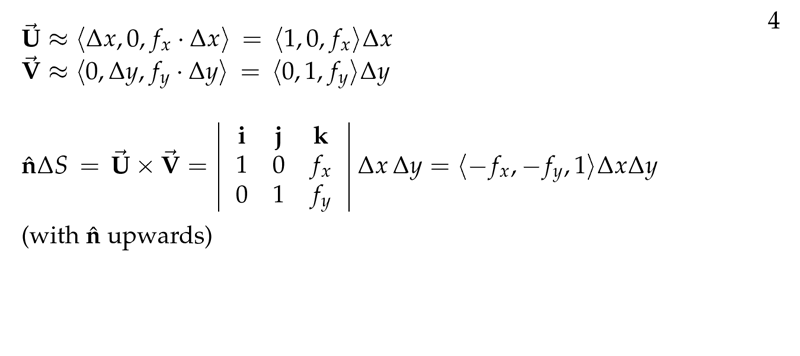
Figure 4: Cross product of surface vectors
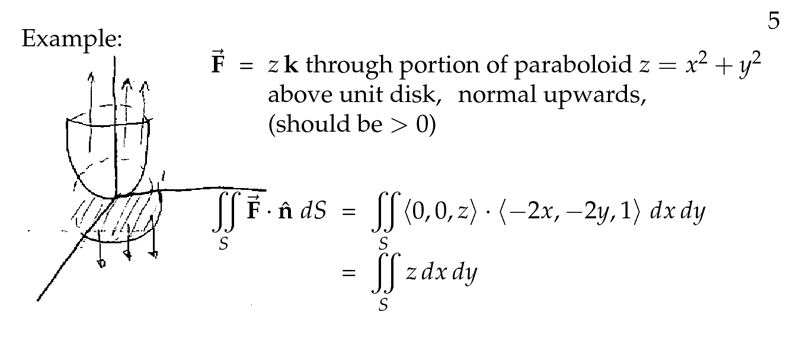
Figure 5: Example of non-trivial surface - I
Figure 6: Example of non-trivial surface - II
2 Which is the flux through general surfaces?
2.1 Front
Which is the flux through general surfaces?
Flux of \(\vb{F}\) through surface \(z = z(x,y)\)
2.2 Back
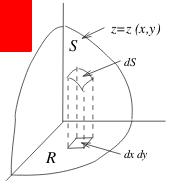
The infinitesimal vector \(\dd{\vb{S}} = \vu{n} \dd{S}\) is simpler to calculate than \(\vu{n}\) and \(\dd{S}\) separately.
\(\dd{\vb{S}} = \ev{- z_x, -z_y, 1} \dd{x} \dd{y}\), where \(\vu{n}\) points “up”
if \(F(x,y,z) = c\) the surface, \({\displaystyle \dd{\vb{S} = \pm \frac{\grad{\vb{F}}}{F_z} \dd{x} \dd{y}}}\)
3 How can we get the \(\dd{\vb{S}}\) formula for general surface?
3.1 Front
How can we get the $\dd{\vb{S}}$ formula for general surface?
Surface: \(z = f(x,y)\). Explain the process to get the final equation
3.2 Back
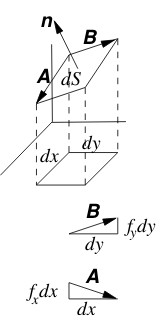
- Region \(R\) is the projection of \(S\) in the \(xy\text{-plane}\)
- Divide up \(R\) into infinitesimal rectangles parallel to \(xy\text{-axes}\)
- \(\dd{S} = \vu{n} \dd{S}\) that means:
- Direction: Perpendicular to the surface, “up” direction
- Magnitude: the area \(\dd{S}\) of the infinitesimal parallelogram
- It’s means a cross product of \(\vb{A} \cross \vb{B}\)
- \(\vb{A} = \ev{\dd{x}, 0, f_x \dd{x}} = \ev{1, 0, f_x} \dd{x}\)
- \(\vb{B} = \ev{0, \dd{y}, f_y \dd{y}} = \ev{0, 1, f_y} \dd{y}\)
- So \(\vb{A} \cross \vb{B} = \ev{-f_x, -f_y, 1} \dd{x} \dd{y}\)
4 Get \(\dd{\vb{S}}\) from the surface given by…
4.1 Front
Get $\dd{\vb{S}}$ from the surface given by…
\(F(x,y,z) = c\) and \(z = z(x,y)\)
In terms of \(\grad{F}\), \(F_x\), \(F_y\) and/or \(F_z\)
4.2 Back
\({\displaystyle F(x,y,z) = c \implies F_x \pdv{x}{x} + F_y \pdv{y}{x} + F_z \pdv{z}{x} = 0 \implies F_x + F_z \pdv{z}{x} = 0}\), so we get that \(\pdv{z}{x} = - \frac{F_x}{F_z}\)
Similarly, we can get \({\displaystyle \pdv{z}{y} = - \frac{F_y}{F_z}}\)
Using \({\displaystyle \dd{\vb{S}} = \ev{- \pdv{z}{x}, - \pdv{z}{y}, 1} \dd{x} \dd{y} = \ev{\frac{F_x}{F_z}, \frac{F_y}{F_z},1} \dd{x} \dd{y} = \frac{\grad{F}}{F_z} \dd{x} \dd{y}}\)
5 Get the \(\dd{\vb{S}}\) for the ellipsoid
5.1 Front
Get the $\dd{\vb{S}}$ for the ellipsoid
\(4x^2 + y^2 + 4z^2 = 4\)
5.2 Back
\({\displaystyle \dd{S} = \frac{\grad{F}}{F_z} \dd{x} \dd{y} = \frac{\ev{8x, 2y, 8z}}{8z}\dd{x} \dd{y} = \ev{\frac{8x}{8z}, \frac{2y}{8z}, 1} \dd{x} \dd{y}}\)
6 How can we use surface integral for compute surface area?
6.1 Front
How can we use surface integral for compute surface area?
6.2 Back
\({\displaystyle \iint_S f(x,y,z) \dd{S} = \iint_S 1 \dd{S}}\) is the area of \(S\)
7 How can calculate mass of the thin shell (of uniform thickness)?
7.1 Front
How can calculate mass of the thin shell (of uniform thickness)?
Density: \(\delta(x,y,z)\) in gms/unit area, shell defined by a surface \(S\)
7.2 Back
Mass of \({\displaystyle S = \iint_S \delta(x,y,z) \dd{S}}\)
8 How can we compute the average value of \(f(x,y,z)\) over the surface \(S\)?
8.1 Front
How can we compute the average value of $f(x,y,z)$ over the surface $S$?
8.2 Back
Average value of \(f\) on \(S\) is \({\displaystyle \frac{1}{area S} \iint_S f(x,y,z) \dd{S}}\)