1 Chalkboard
Figure 1: Flux on not constant \(\vb{F} \cdot \vu{n}\)
Figure 2: \(\dd{S}\) in spherical coordinates
Figure 3: Computing flux

Figure 4: Finding \(\vu{n}\dd{S}\) - I

Figure 5: Finding \(\vu{n}\dd{S}\) - II

Figure 6: Finding \(\vu{n}\dd{S}\) - III

Figure 7: Geometric interpretation of flux when \(\vb{F}\) is velocity field
2 How is the surface of the equation \(x^{2}+y^{2}=a^2\) in 3 space?
2.1 Front
How is the surface of the equation $x^{2}+y^{2}=a^{2}$ in 3 space?
Describe it and write it’s normal unit vector
2.2 Back
It’s a infinite cylinder
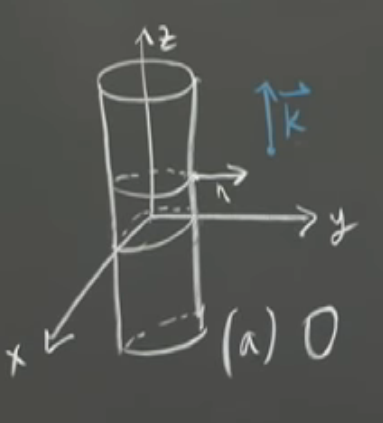
\(\vu{n} = \frac{1}{a} (x \vu{i} + y \vu{j})\), there no \(\vu{k}\) component
3 How is the surface?
3.1 Front
How is the surface?
\(x^{2} + y^{2} + z^{2} = 1\), where \(z > 0\)
3.2 Back
Is the upper half-sphere
4 How is the surface \(x+z=1\) for which \(x>0\), \(z>0\), \(0<y<1\)?
4.1 Front
How is the surface $x+z=1$ for which $x>0$, $z>0$, $0<y<1$?
Describe it an write it’s normal unit vector
4.2 Back
Is a rectangle in the first octant, \({\displaystyle \vu{n} = \frac{1}{\sqrt{2}} \ev{1, 0, 1}}\)
5 Describe the surface element and unit normal vector for a cylinder?
5.1 Front
Describe the surface element and unit normal vector for a cylinder?
Cylinder: \(x^2 + y^2 = a^2\)
5.2 Back
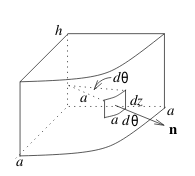
\(\dd{S} = a \dd{\theta} \dd{z}\)
Normal unit vector: \({\displaystyle \vu{n} = \pm \frac{1}{a} \ev{x,y,0}}\)
It’s recommendable compute first \(\vb{F} \cdot \vu{n}\), and then convert to cylindrical coordinate system.
- \(x = a \cos \theta\)
- \(y = a \sin \theta\)
- \(z = z\)
6 Describe the surface element and unit normal vector for a sphere?
6.1 Front
Describe the surface element and unit normal vector for a sphere?
Sphere: \(x^2 + y^2 + z^2 = a^2\)
6.2 Back
Using spherical coordinates system
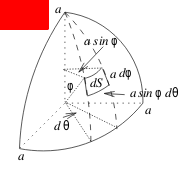
\(\dd{S} = a^2 \sin \phi \dd{\phi} \dd{\theta}\)
\({\displaystyle \vu{n} = \pm \frac{1}{a} \ev{x,y,z}}\)
- \(x = a \sin \phi \cos \theta\)
- \(y = a \sin \phi \sin \theta\)
- \(z = a \cos \phi\)
It’s recommended compute \(\vb{F} \cdot \vu{n}\) before converting to spherical coordinates
7 Describe the surface element and unit normal vector for a horizontal plane?
7.1 Front
Describe the surface element and unit normal vector for a horizontal plane?
Plane: \(z = a\)
7.2 Back
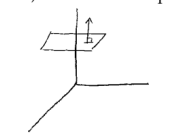
\(\vu{n} = \pm \ev{0,0,1} = \pm \vu{k}\)
\(\dd{S} = \dd{x} \dd{y}\)
8 Can you reduce this expression?
8.1 Front
Can you reduce this expression?
\({\displaystyle \vb{F} \cdot \vu{n} = \frac{x^2 z + y^2 z + z^3}{a}}\), in a sphere of radius \(a\)
8.2 Back
\(az\)
Using: \(x^2 + y^2 + z^2 = a^2\)