1 Chalkboard
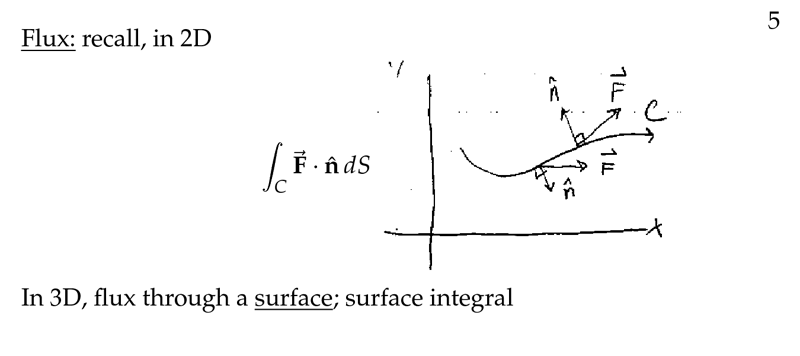
Figure 1: Recall flux in 2D
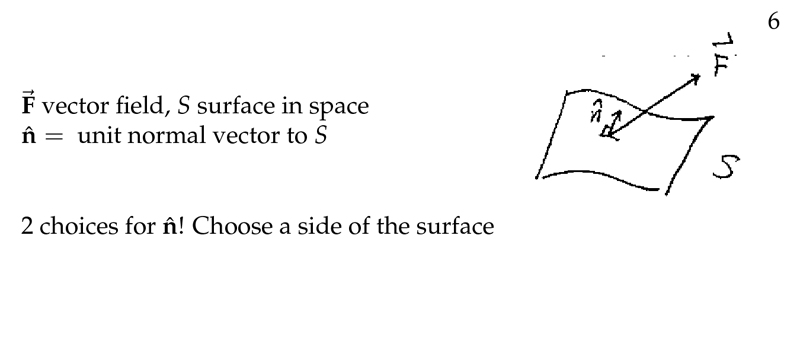
Figure 2: Flux of \(\vb{F}\) across \(\Delta S\)
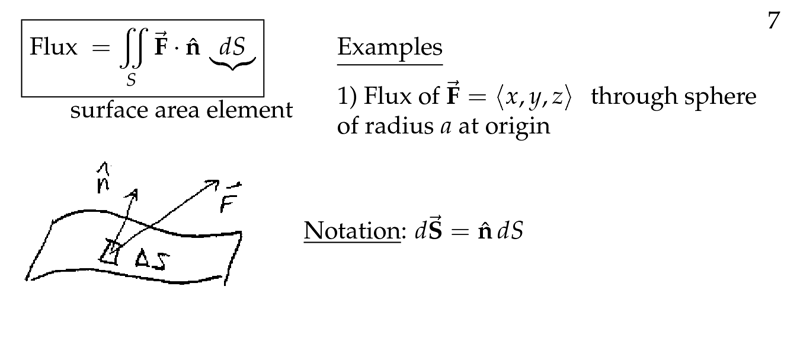
Figure 3: Flux of \(\vb{F}\) across the surface
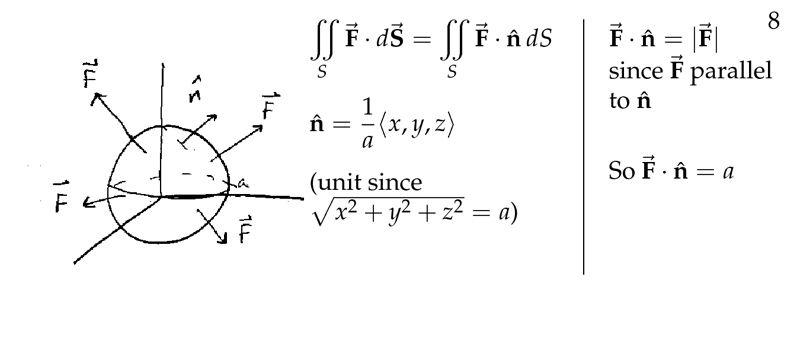
Figure 4: Example the flux across the sphere
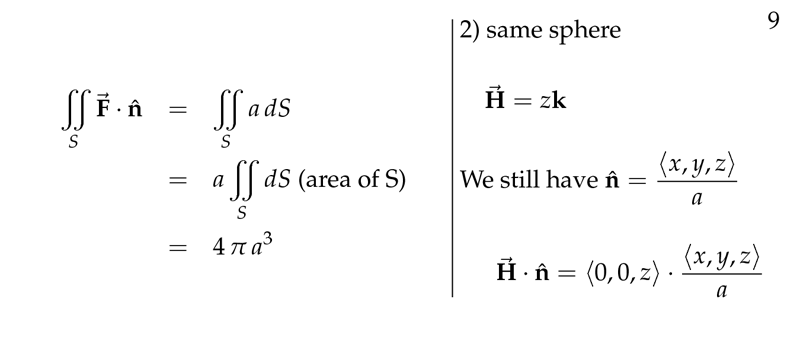
Figure 5: Example the flux across the sphere - II
2 Which is the difference between surface integral and line integral?
2.1 Front
Which is the difference between surface integral and line integral?
2.2 Back
Surface integral are a natural generalization of line integrals: instead of integrating over a curve, we integrate over a surface in 3-space.
3 How looks like a surface integral?
3.1 Front
How looks like a surface integral?
of the continuous function \(f(x,y,z)\) over the surface \(S\)
3.2 Back
\({\displaystyle \iint_S f(x,y,z) \dd{S}}\)
4 Why a surface integral is a double integral?
4.1 Front
Why a surface integral is a double integral?
of the continuous function \(f(x,y,z)\) over the surface \(S\)
4.2 Back
You divide up the surface in small pieces \(\Delta S_i\), pick a point \((x_i, y_i, z_i)\) in the \(i\) -th piece, so the Riemman Sum is:
\({\displaystyle \lim_{n \to \infty} \sum_{i=0}^n f(x_i, y_i, z_i) \Delta S_i = \iint_S f(x,y,z) \dd{S}}\)
Note: The surface has to be smooth and not infinite in extent
5 What is the surface integral for flux?
5.1 Front
What is the surface integral for flux?
Vector field \(\vb{F}(x,y,z)\), oriented surface \(S\)
5.2 Back
Using the positively directed unit normal vector \(\vu{n}\)
flux of \(\vb{F}\) through \(S\)
\({\displaystyle \iint_S (\vb{F} \cdot \vu{n}) \dd{S} = \iint_S \vb{F} \cdot \dd{\vb{S}}}\)
where \(\dd{\vb{S} = \vu{n} \dd{S}}\)
6 How can we orientate a surface?
6.1 Front
How can we orientate a surface?
6.2 Back
Surface \(S\) has 2 sides and one of them has been designated to be the positive side. There is no convention about it, but the up side is the positive one.
If the surface is closed, like a sphere or cube, by convention it is oriented so that the outer side is the positive one. So that \(\vu{n}\) points towards the outside of \(S\)
7 What is the net flow rate across \(S\)
7.1 Front
What is the net flow rate across $S$
\(\vb{F}\) is velocity field to the flow
7.2 Back
The flow is an incompressible fluid of density constant
It the flux of \(\vb{F}\) across \(S\), its equations is
\({\displaystyle \iint_S \vb{F} \cdot \dd{\vb{S}}}\)
It’s positive when the \(\vb{F}\) in the direction of \(\vu{n}\)
8 What represent \(\vb{F} \cdot \vu{n}\) and \(\vb{F} \cdot \vu{n} \dd{S}\)?
8.1 Front
What represent $\vb{F} \cdot \vu{n}$ and $\vb{F} \cdot \vu{n} \dd{S}$?
If \(\vb{F}\) is the velocity field for the flow of an incompressible fluid of density \(1\)
8.2 Back
- \(\vb{F} \cdot \vu{n}\) represents the component of the velocity in the positive perpendicular direction to the surface
- \(\vb{F} \cdot \vu{n} \dd{S}\) represents the flow rate across the little infinitesimal piece of surface having area \(\dd{S}\)
9 What is the net mass transport rate of fluid across \(S\)
9.1 Front
What is the net mass transport rate of fluid across $S$
per unit area, per time unit
9.2 Back
Is the flux of \(F\) through \(S\) for the fluid with varying density, then \(\vb{F} = \delta(x,y,z) \vb{v}\).
\({\displaystyle \iint_S \vb{F} \cdot \dd{\vb{S}}}\)