1 Chalkboard

Figure 1: Vector fields in space

Figure 2: Force fields
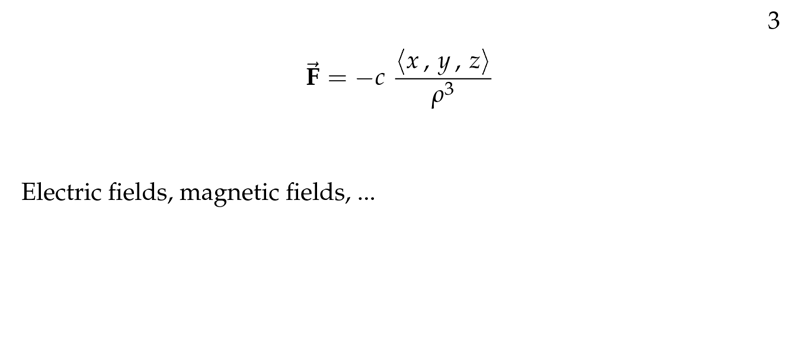
Figure 3: Graviational field equation and more examples
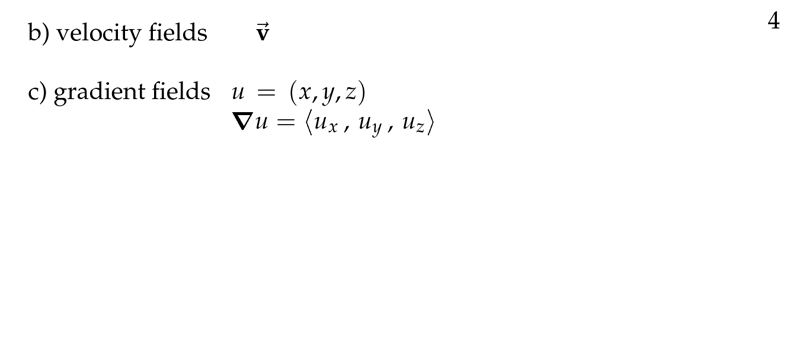
Figure 4: Velocity and gradient fields
2 What is a force field in 3-space?
2.1 Front
What is a force field in 3-space?
For example, gravitational, electrostatic, electromagnetic, …
2.2 Back
At the point \((x_0, y_0, z_0)\) we place the vector having the direction and magnitude of the force which the field would exert on an unit test particle placed at the point
3 What is a flow field in 3-space?
3.1 Front
What is a flow field in 3-space?
Assume the motion is steady-state
3.2 Back
We allow sources and sinks, but in 3-space you can’t add from four-dimensional. We could think of thin pipes inserted into the domain at various points adding and removing fluid.
\(\vb{F} = \delta \vb{v}\), where \(\delta(x,y,z)\) is the density of the fluid, and \(\vb{v}\) is the velocity fields.
The velocity field \(\vb{v}\) gives the direction and magnitude (speed) of the flow at any point \((x,y,z)\)
- dir \(\vb{F}\) is the direction of flow
- \(\abs{F}\) is the mass transport rate (per unit area) at \((x,y,z)\) in the flow direction. Rate per unit area at which mass is transported across a small piece of plane perpendicular to the flow at the point \((x,y,z)\)
4 Find velocity field of a fluid rotating with constant angular velocity \(w\)
4.1 Front
Find velocity field of a fluid rotating with constant angular velocity $w$
Around \(z\text{-axis}\), in the direction given by the right-hand rule, when thumb points in the \(\vu{k}\) direction
4.2 Back
- Flow doesn’t depend on \(z\)
- \(\abs{\vb{v}} = wr\)
\(\vb{F}(x,y,z) = \vb{v} = w (-y \vu{i} + x \vu{j})\)
5 Find velocity field of a fluid rotating with constant angular velocity \(w\)
5.1 Front
Find velocity field of a fluid rotating with constant angular velocity $w$
Around \(y\text{-axis}\), in the direction given by the right-hand rule, when thumb points in the \(\vu{j}\) direction
5.2 Back
- Flow doesn’t depend on \(y\)
- \(\abs{\vb{v}} = wr\)
- The flow in the \(xz\text{-plane}\) is clockwise, when positive \(x\) and \(z\) axes are drawn so as to give a right-handed system
\(\vb{F}(x,y,z) = \vb{v} = w (z \vu{i} - x \vu{k})\)
6 Find the 3-dimensional flow field of a gas streaming radially outward
6.1 Front
Find the 3-dimensional flow field of a gas streaming radially outward
with constant velocity from a source at the origin of constant strength
6.2 Back
- The area of the sphere increases like the square of it’s radius
- Constant velocity, the density of flow must decrease like \(1/\rho^{2}\) as you go out from origin
\(\vb{F}(x,y,z) = \delta \vb{v} = \frac{c_1}{\rho^2} \frac{c_2 (x \vu{i} + y \vu{j} + z \vu{k})}{\rho} = \frac{c (x \vu{i} + y \vu{j} + z \vu{k})}{\rho^3}\)
In the 2-dimensional case, the field magnitude decrease like \(1/r\) as you go out from origin
7 If \(\vb{F}\) is a flow field where the density is constant
7.1 Front
If $\vb{F}$ is a flow field where the density is constant
How the flow speed change, in 2 and 3 dimensions
The source at the origin of constant strength
7.2 Back
Is the flow density is constant, the fluid is incompressible so the flow speed must decrease
- \(c/r\) in 2 dimension
- \(c/\rho^2\) in 3 dimension
as you go out from the origin
8 If \(\vb{F}\) is a flow field where the flow speed is constant
8.1 Front
If $\vb{F}$ is a flow field where the flow speed is constant
how must change density in 2 and 3 dimension
The source at the origin of constant strength
8.2 Back
If the flow speed stays constant and the fluid is compressible like a gas, the density must decrease
- \(c/r\) in 2 dimensions
- \(c/\rho^2\) in 3 dimensions
as you go out from the origin