1 Chalkboard
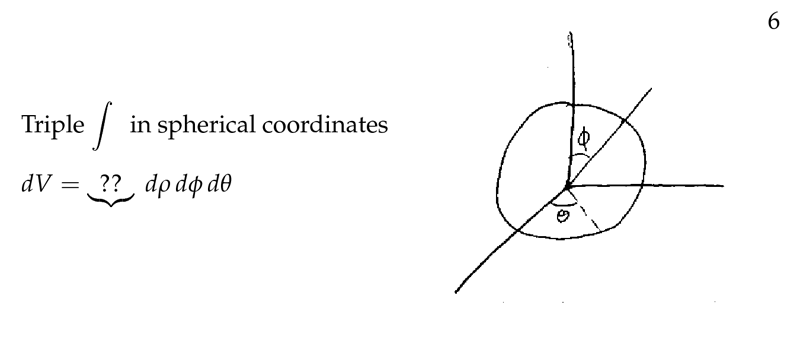
Figure 1: Triple integral in spherical coordinates
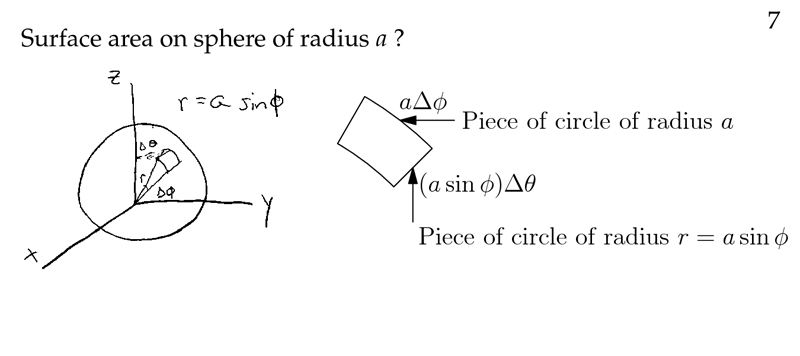
Figure 2: Surface area on sphere of radius \(a\)
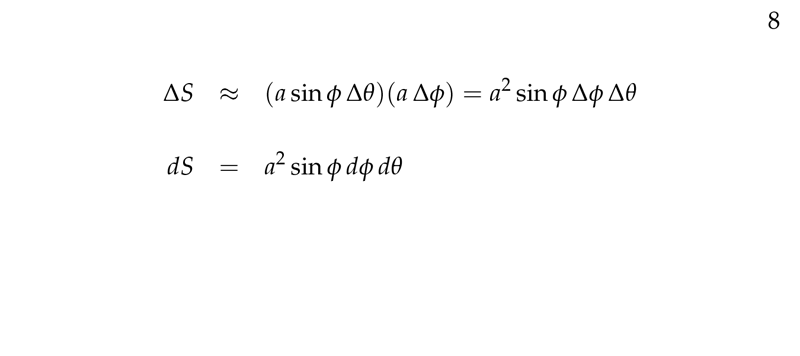
Figure 3: Surface element
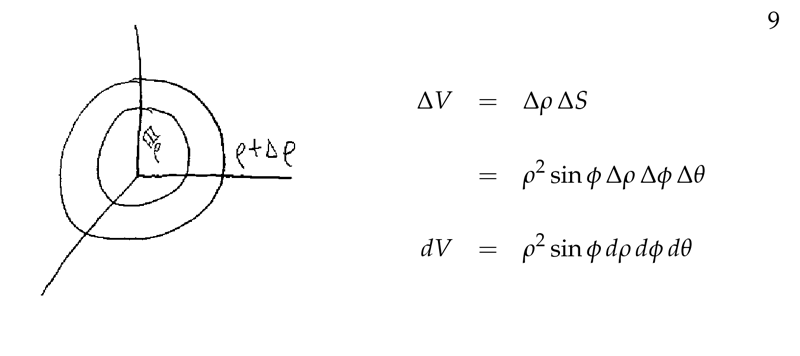
Figure 4: Volume element
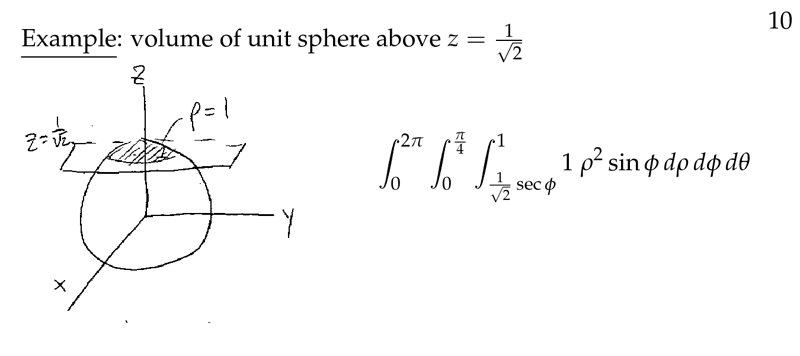
Figure 5: Example of volume of unit sphere above \(z = 1 / \sqrt{2}\)
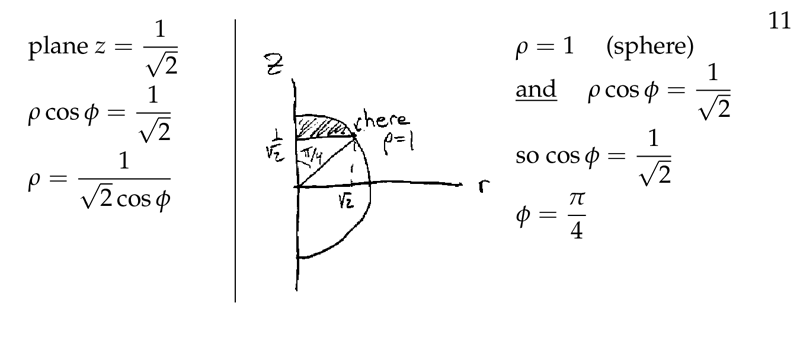
Figure 6: Example: View at \(zr\text{-plane}\)

Figure 7: Evaluation
2 How is a vector field in space?
2.1 Front
How is a vector field in space?
2.2 Back
\(\vb{F}\) is a vector field where for each point \((x_0, y_0, z_0)\) has assigned a vector \(\vb{F}(x_0, y_0, z_0)\) where \(M,N,P\) are all defined.
\(\vb{F}(x,y,z) = M(x,y,z) \vu{i} + N(x,y,z)\vu{j} + P(x,y,z)\vu{k}\)
3 When can we say that \(\vb{F}\) in space is continuously differentiable?
3.1 Front
When can we say that $\vb{F}$ in space is continuously differentiable?
In some domain \(D\) of 3-space
3.2 Back
\(\vb{F} = \ev{M,N,P}\) if all 9 first partial derivatives exits and are continuous in \(D\)
- \(M_x\), \(M_y\), \(M_z\)
- \(N_x\), \(N_y\), \(N_z\)
- \(P_x\), \(P_y\), \(P_z\)
4 What that means that the motions is steady-state?
4.1 Front
What that means that the motions is steady-state?
For example, in flow or velocity fields
4.2 Back
It is when the direction and magnitude of the flow at any point does not change over time