1 Chalkboard
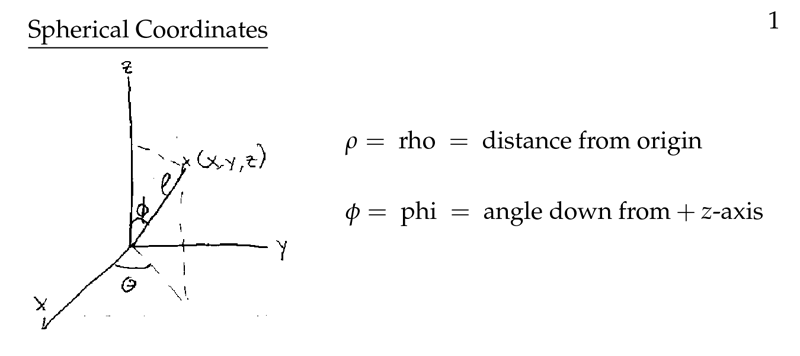
Figure 1: Spherical coordinates
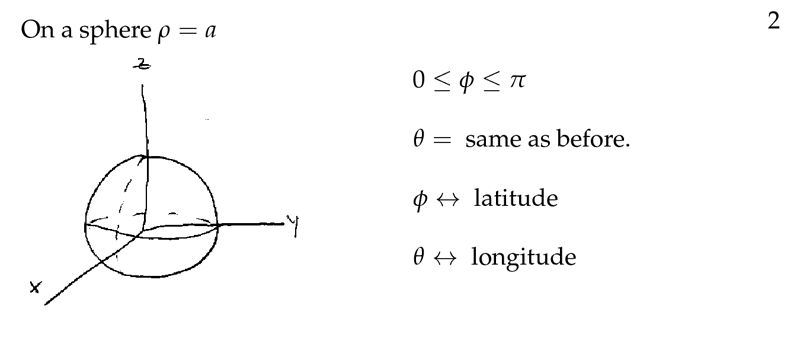
Figure 2: On a sphere \(\rho = a\)
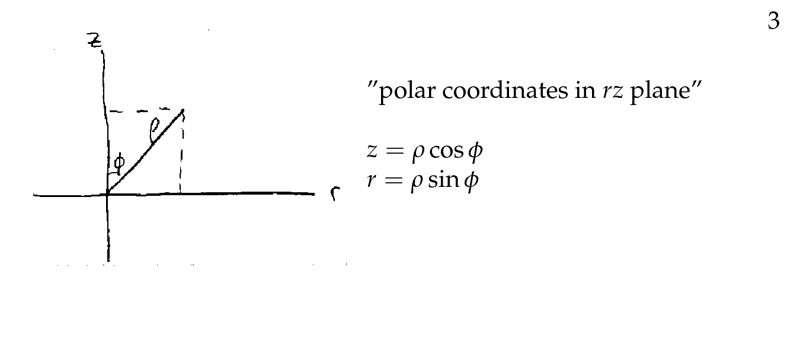
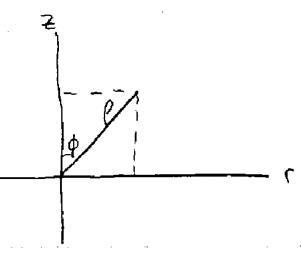
Figure 3: Transform from cylindrical to spherical coordinates
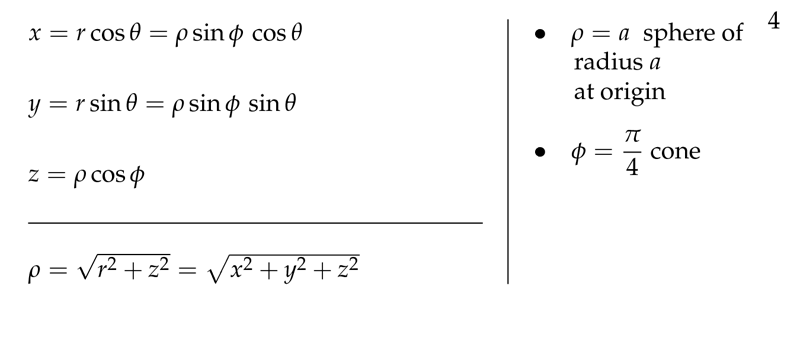
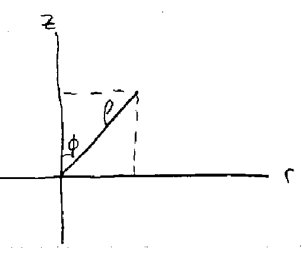
Figure 4: Transform from spherical to rectangular coordinates
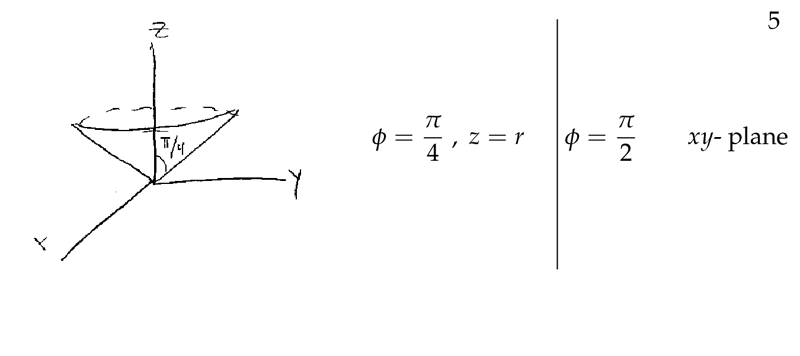
Figure 5: Examples of figures on spherical coordinates
2 How is defined the spherical coordinates?
2.1 Front
How is defined the spherical coordinates?
Draw coordinates setting and define limit conventions
2.2 Back
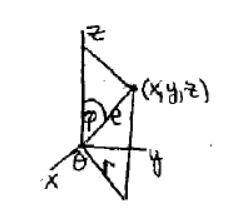
- \(\rho\) is the distance to the origin \(\rho > 0\)
- \(\phi\) is angle to \(z\text{-axis}\), \(0 \leq \phi \leq \pi\)
- \(\theta\) is the \(\theta\) on polar coordinates, the angle of projection to \(xy\text{-plane}\) with \(x\text{-axis}\), \(0 \leq \theta \leq 2 \pi\)
3 How to convert from spherical coordinates to rectangular coordinates
3.1 Front
How to convert from spherical coordinates to rectangular coordinates
3.2 Back
Using cylindrical coordinates, where \(r = \rho \sin \phi\), and \(x = r \cos \theta\) and \(y = r \sin \theta\)
- \(x = \rho \sin \phi \cos \theta\)
- \(y = \rho \sin \phi \sin \theta\)
- \(z = \rho \cos \phi\)
4 How can we write cylindrical coordinates in terms of spherical coordinates?
4.1 Front
How can we write cylindrical coordinates in terms of spherical coordinates?
4.2 Back
- \(r = \rho \sin \phi\)
- \(z = \rho \cos \phi\)
\(\theta\) is the same angle
5 Write \(\rho\) of spherical coordinates in terms of rectangular coordinates?
5.1 Front
Write $\rho$ of spherical coordinates in terms of rectangular coordinates?
5.2 Back
\(\rho = \sqrt{x^2 + y^2 + z^2}\)
6 Write \(\phi\) in terms of rectangular coordinates
6.1 Front
Write $\phi$ in terms of rectangular coordinates
6.2 Back
\(\phi = \arccos (\frac{z}{\rho}) = \arccos (\frac{z}{\sqrt{x^2 + y^2 + z^2}})\)
7 Write \(\theta\) in terms of rectangular coordinates
7.1 Front
Write $\theta$ in terms of rectangular coordinates
7.2 Back
\(\theta = \arctan (y/x)\)
8 Which is the volume element in spherical coordinates?
8.1 Front
Which is the volume element in spherical coordinates?
8.2 Back
Surface area
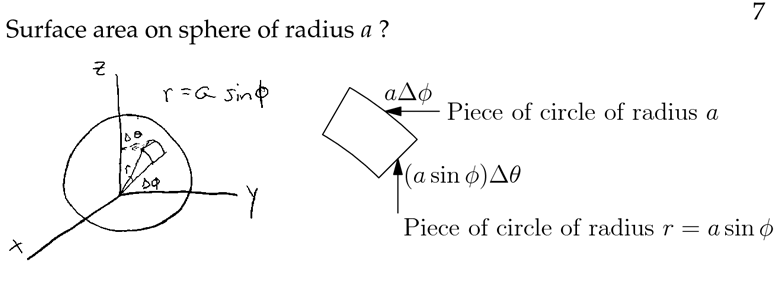
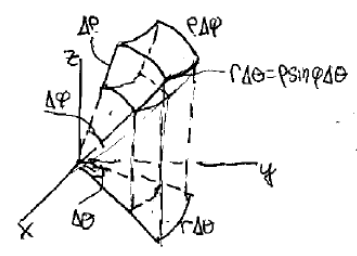
It’s a cube formed by:
- \(\Delta \rho\)
- \(\Delta S\) (delta surface)
- \(\rho \Delta \phi\)
- \(r \Delta \theta = \rho \sin \phi \Delta \theta\)
\(\dd{V} = \rho^2 \sin \phi \dd{\rho} \dd{\phi} \dd{\theta}\)
9 How can we find limit of integrals in spherical coordinates?
9.1 Front
How can we find limit of integrals in spherical coordinates?
9.2 Back
\({\displaystyle \iiint_D \dd{\rho} \dd{\phi} \dd{\theta}}\)
- Hold \(\phi\) and \(\theta\) fixed, integrating first with respect to
\(\rho\)
- Check where \(\rho\) enter and exit to \(D\)
- Hold \(\theta\) fixed, integrating with respect to \(\phi\)
- Integrate over the values where \(\phi\) which rays intersect \(D\)
- Supply limits on \(\theta\)
10 Setup up triple integral in spherical coordinates
10.1 Front
Setup up triple integral in spherical coordinates
Circle in \(yz\text{-plane}\) of radius \(1\) and center \((1,0)\), rotate it about \(z\text{-axis}\) and take \(D\) to be that part of the resulting solid lying in the first octant
10.2 Back
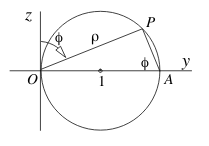
- Check the circle and get values for \(\rho\) and \(\phi\)
- Right triangle where \(OAP = \phi\), both angles are complementary
- \(\rho = 2 \sin \phi\)
- This circle rotate around \(z\text{-axis}\), so \(\rho = 2 \sin \phi\) si the equation of the whole surface
- Let \(\phi\) and \(\theta\) fixed
- \(\rho\) enters to \(D\) from \(\rho = 0\) and leaves when \(\rho = 2 \sin \phi\)
- Let \(\theta\) fixed
- \(\phi\) the rays enters at \(\phi = 0\) and leaves at \(\phi = \pi / 2\) (Consider only first octant, above \(xy\text{-plane}\))
- \(\theta\) enter at \(\theta = 0\) and leave at \(\theta = \pi / 2\) (First octant)
\({\displaystyle \int_0^{\pi/2} \int_0^{\pi/2} \int_0^{2 \sin \phi} \dd{V} = \int_0^{\pi/2} \int_0^{\pi/2} \int_0^{2 \sin \phi} \rho^2 \sin \phi \dd{\rho} \dd{\phi} \dd{\theta}}\)
11 Which is the distance to any point in spherical coordinates?
11.1 Front
Which is the distance to any point in spherical coordinates?
11.2 Back
It’s \(\rho\) directly, in rectangular coordinates:
\(\rho = \sqrt{x^2 + y^2 + z^2}\)
12 How can we apply a changing coordinates in triple integrals?
12.1 Front
How can we apply a changing coordinates in triple integrals?
- \(u = u(x,y,z)\)
- \(v = v(x,y,z)\)
- \(w = w(x,y,z)\)
12.2 Back
Applying the expression
\({\displaystyle \dd{V} = \abs{\pdv{(x,y,z)}{(u,v,w)}} \dd{u} \dd{v} \dd{w}}\)
Where the key factor is the Jacobian
\({\displaystyle \pdv{(x,y,z)}{(u,v,w)} = \begin{vmatrix}x_u & x_v & x_w \ y_u & y_v & y_w \ z_u & z_v & v_w \end{vmatrix}}\) x