1 Chalkboard
Figure 1: Mass on triple integral
Figure 2: Average value on triple integral
Figure 3: Center of mass on triple integral
Figure 4: Moment of inertia on triple integral
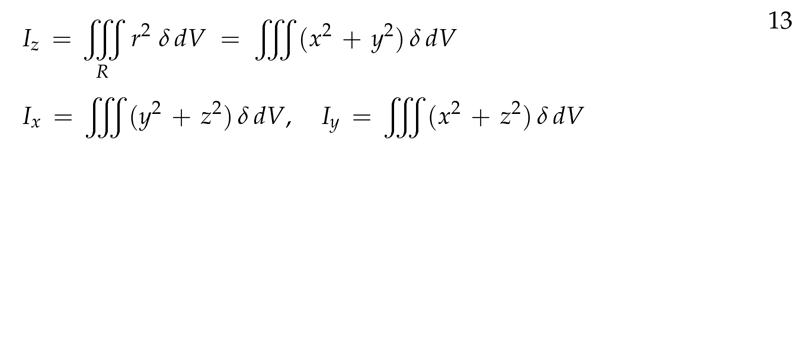
Figure 5: Moment of inertia about axis
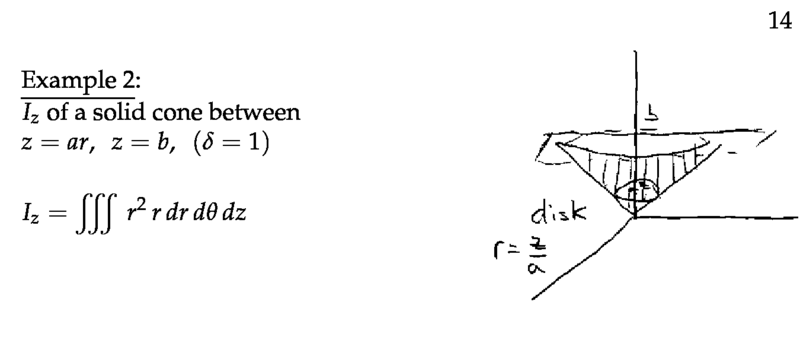
Figure 6: Moment of inertia of a solid cone
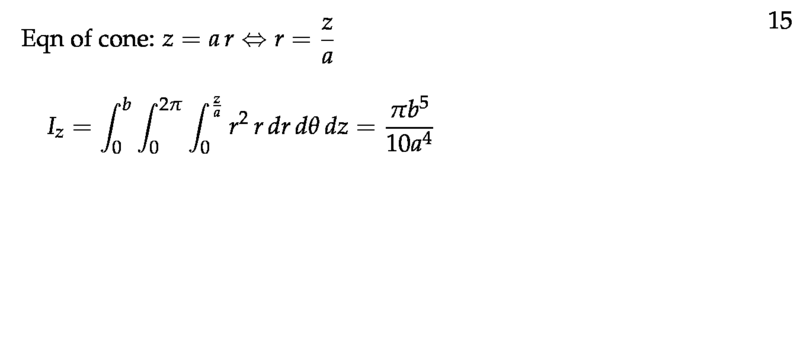
Figure 7: Moment of inertia of a solid cone - II
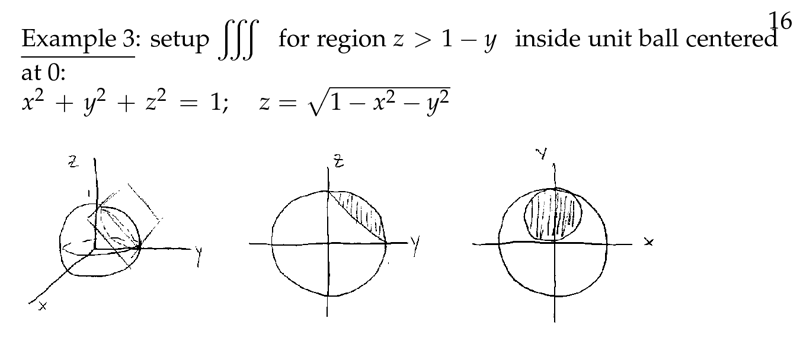
Figure 8: Example of volume
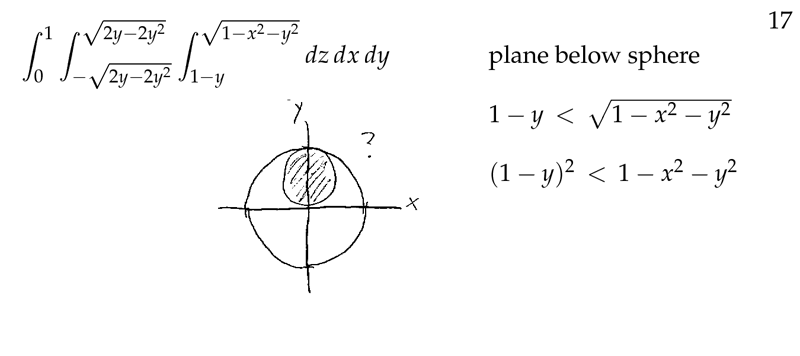
Figure 9: Setting up triple integral for volume
2 What is the center of mass of a solid figure?
2.1 Front
What is the center of mass of a solid figure?
2.2 Back
Center of mass is a point \((\bar{x}, \bar{y}, \bar{z})\)
Mass: \({\displaystyle \iiint_D \delta(x,y,z) \dd{V}}\)
- \({\displaystyle \bar{x} = \frac{1}{\text{Mass}} \iiint_D x \delta(x,y,z) \dd{V}}\)
- \({\displaystyle \bar{y} = \frac{1}{\text{Mass}} \iiint_D y \delta(x,y,z) \dd{V}}\)
- \({\displaystyle \bar{z} = \frac{1}{\text{Mass}} \iiint_D z \delta(x,y,z) \dd{V}}\)
3 What is the average value of \(f(x,y,z)\) in \(R\)?
3.1 Front
What is the average value of $f(x,y,z)$ in $R$?
Let \(R\) be a 3D space region
3.2 Back
\({\displaystyle \bar{f} = \frac{1}{\text{Volume}} \iiint_R f(x,y,z) \dd{V}}\)
4 What is the weighted average of \(f(x,y,z)\) in \(R\)
4.1 Front
What is the weighted average of $f(x,y,z)$ in $R$
Weighted function: \(\delta(x,y,z)\)
4.2 Back
\({\displaystyle \bar{f} = \frac{1}{\iiint_R \delta(x,y,z) \dd{V}} \iint_R f(x,y,z) \delta(x,y,z) \dd{V}}\)