1 Chalkboard
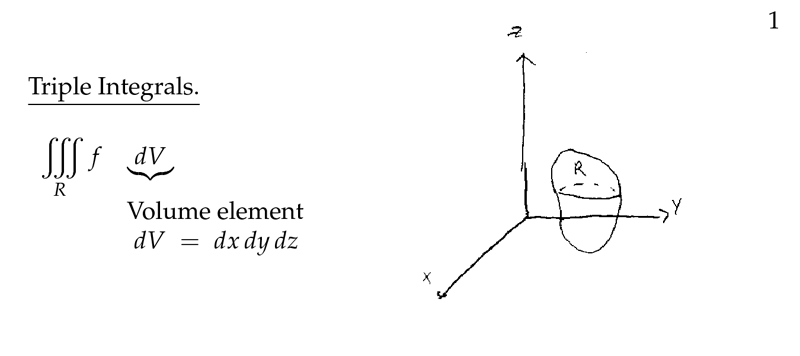
Figure 1: Triple integrals
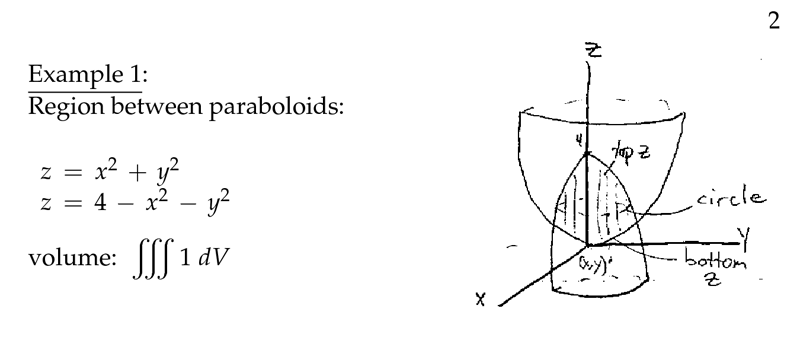
Figure 2: Example of triple integral
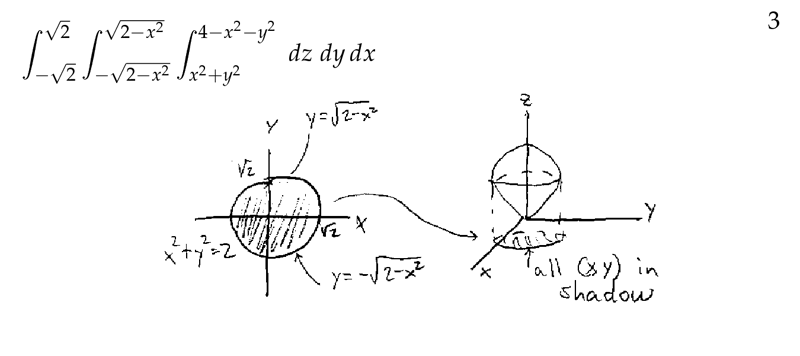
Figure 3: Setting up interated integral for triple integral
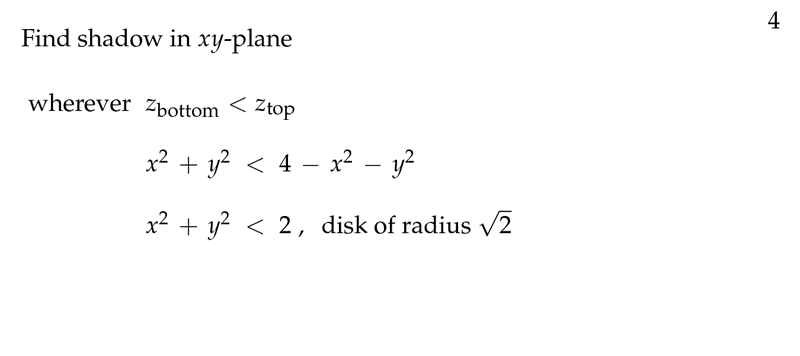
Figure 4: Find shadow in \(xy\text{-plane}\)
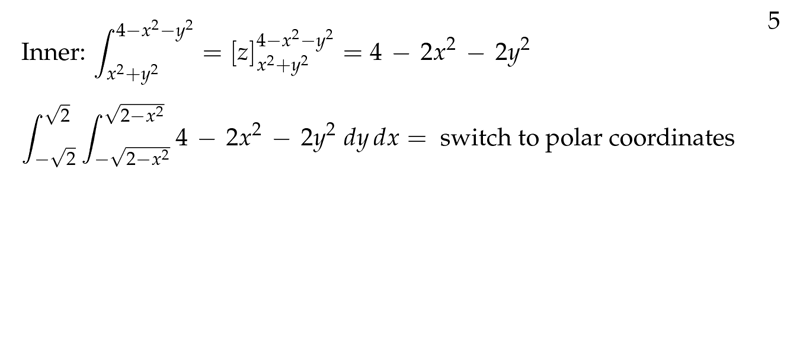
Figure 5: Computing iterated integral

Figure 6: Better use polar coordinates for triple coordinates
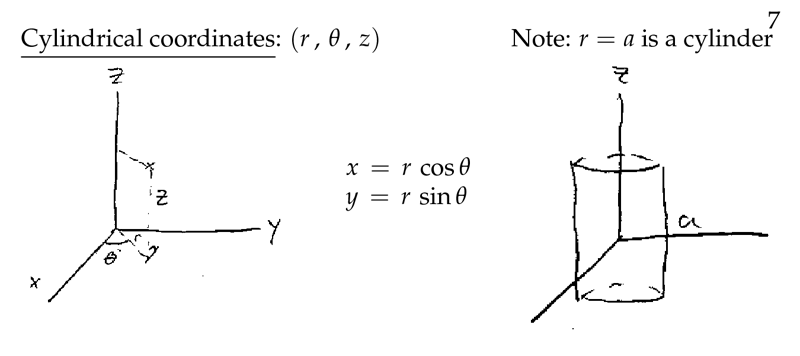
Figure 7: Cylindrical coordinates \((r, \theta, z)\)
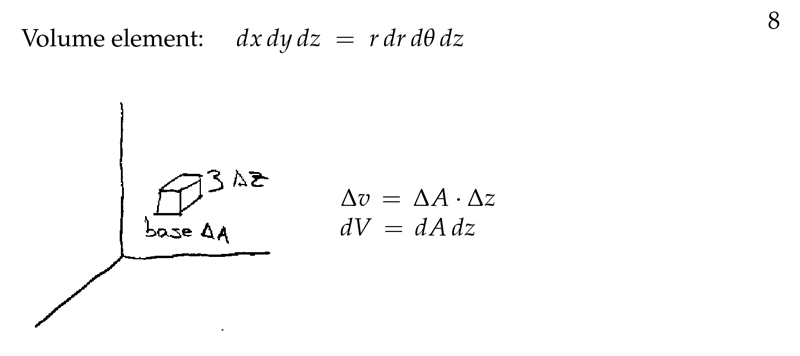
Figure 8: Volumen element
2 What is a triple integral in rectangular coordinates?
2.1 Front
What is a triple integral in rectangular coordinates?
2.2 Back
\({\displaystyle \iiint_D \dd{z} \dd{y} \dd{x}}\)
3 How to supply limits for a triple integral?
3.1 Front
How to supply limits for a triple integral?
Over a region \(D\)
3.2 Back
- Hold \(x\) and \(y\) fixed and let \(z\) increase (Vertical line)
- Integrate from the \(z\text{-value}\) where the vertical line enters the region \(D\) to the \(z\text{-value}\) where it leaves \(D\)
- Supply the remaining limits (in either \(xy\text{-coordinates}\) or polar coordinates) so that you include all vertical lines which intersect \(D\). It’s like a double integral
4 How can we find the projection of \(D\) onto the \(xy\text{-plane}\)?
4.1 Front
How can we find the projection of $D$ onto the $xy\text{-plane}$?
\({\displaystyle \iiint_D \dd{z} \dd{y} \dd{x} = \iint_R \int_{x^2 + y^2}^{4 - x^2 -y^2} \dd{z} \dd{A}}\)
\(D\) is a region lying between the paraboloids, \(z = x^2 + y^2\) and \(z = 4 -x^2 -y^2\)
4.2 Back
We find this curve by eliminating \(z\) from the two equation which define the region in 3D. And solve in one equation
- \(z_{\text{bottom} < z_{\text{top}}}\)
- \(x^2 + y^2 < 4 - x^2 - y^2\)
- \(x^2 + y^2 < 2\) (Disk of radius \(\sqrt{2}\))
5 Which is the volume element in triple integral?
5.1 Front
Which is the volume element in triple integral?
In rectangular and cylindrical coordinates
5.2 Back
In rectangle coordinates: \(\dd{z} \dd{y} \dd{x}\)
In cylindrical coordinates \(\dd{z} r \dd{r} \dd{\theta}\)
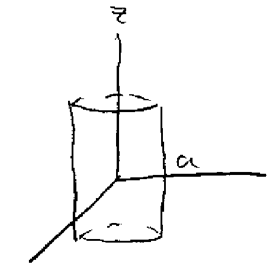
6 What is the cylindrical coordinates?
6.1 Front
What is the cylindrical coordinates?
6.2 Back
Has 3 components: \(r, \theta, z\)
- \(x = r \cos \theta\)
- \(y = r \sin \theta\)
So, \(x,y\) coordinates can be converted as polar coordinates, and using \(z\) as vertical line of the cylinder
7 Setting up the triple integral
7.1 Front
Setting up the triple integral
Moment of inertia about the \(z\text{-axis}\) of a solid bounded by the paraboloid \(z=x^2 + y^2\) and the plane \(z=1\). Uniform density \(\delta = 1\)
- In this order: \(\dd{r} \dd{\theta} \dd{z}\)
7.2 Back
\({\displaystyle \int_0^1 \int_0^{2\pi} \int_0^{\sqrt{z}} r^2 r \dd{r} \dd{\theta} \dd{z}}\)