1 Chalkboard

Figure 1: More about validity of Green’s Theorem

Figure 2: \(\vb{F}\) defined everywhere in \(R\)
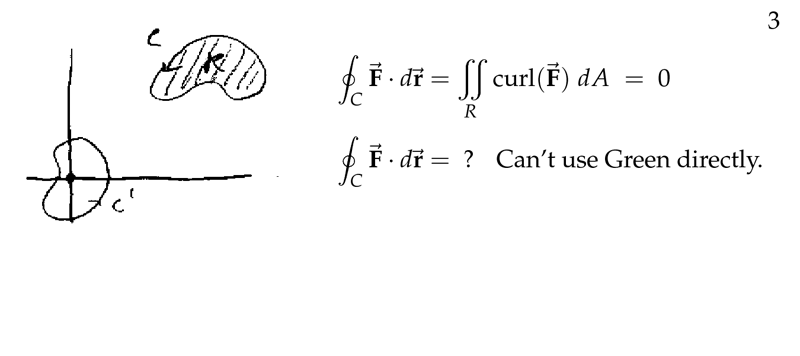
Figure 3: Use of Green’s Theorem
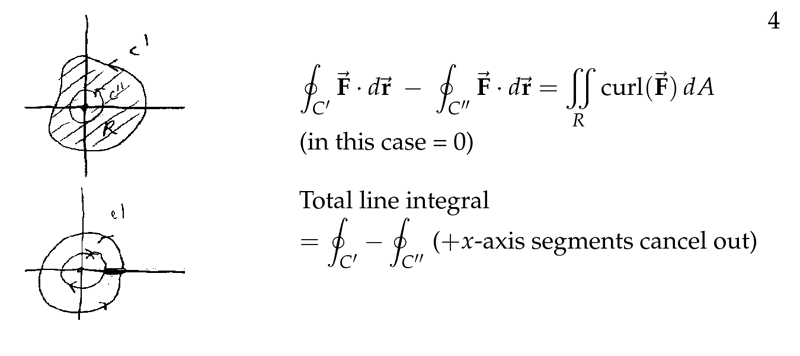
Figure 4: Remove the region where \(\vb{F}\) is not defined
2 What happens when \(C\) is positively oriented but not simple
2.1 Front
What happens when $C$ is positively oriented but not simple
Let \({\displaystyle \vb{F} = \frac{-y \vu{i} + x \vu{j}}{x^2 + y^2}}\), and the region inside \(C\) contains the origin.
Tip: \(\text{curl} \vb{F} = 0\)
2.2 Back
We can break \(C\) into two curves around the origin at a point where it crosses.
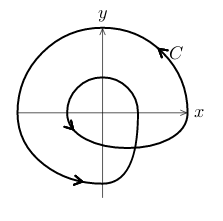
Repeating this as often as necessary, we find that \({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = 2\pi n}\), where \(n\) is the number of times \(C\) goes counterclockwise around \((0,0)\)
If \(C\) is negatively oriented, \({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}} = - \oint_{C’} \vb{F} \cdot \dd{\vb{r}}}\), where \(C’\) is an oppositely oriented copy of \(C\)
3 How can we apply the Green’s Theorem to this region?
3.1 Front
How can we apply the Green’s Theorem to this region?
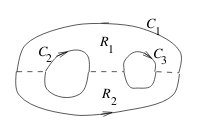
Write its equations
3.2 Back
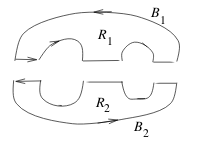
Letting \(B_1\) and \(B_2\) be the boundary curves
- \({\displaystyle \oint_{B_1} \vb{F} \cdot \dd{\vb{r}} = \iint_{R_1} \text{curl} \vb{F} \dd{A}}\)
- \({\displaystyle \oint_{B_2} \vb{F} \cdot \dd{\vb{r}} = \iint_{R_2} \text{curl} \vb{F} \dd{A}}\)
Add these two equations together, so we get the extended Green’s Theorem. The three cuts, there are two line integrals taken in opposite directions, which therefore cancel each other out
4 Green’s Theorem for a region boundary by several simple curves
4.1 Front
Green’s Theorem for a region boundary by several simple curves
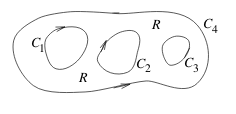
4.2 Back
\({\displaystyle \int_{C_1} \vb{F} \cdot \dd{\vb{r}} + \dots + \int_{C_m} \vb{F} \cdot \dd{\vb{r}} = \iint_R \text{curl} \vb{F} \dd{A}}\)
Check that each part of the boundary oriented so the normal \(\vu{n}\) points outside \(R\)
5 What could mean if we use Green’s Theorem in normal form for this region?
5.1 Front
What could mean if we use Green’s Theorem in normal form for this region?
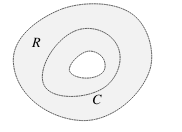
Some region \(R\) where \(\vb{F}\) is defined with a hole inside a closed curve \(C\). \(\vb{F}\) is conservative
5.2 Back
If \(\text{div} \vb{F} = 0\) everywhere except at the hole, it doesn’t guarantee that the flux through every closed curve will be 0
For this spot where \(\text{div} \vb{F}\) is undefined might be a source, through which fluid is being added to the flow (or poured).