1 Chalkboard
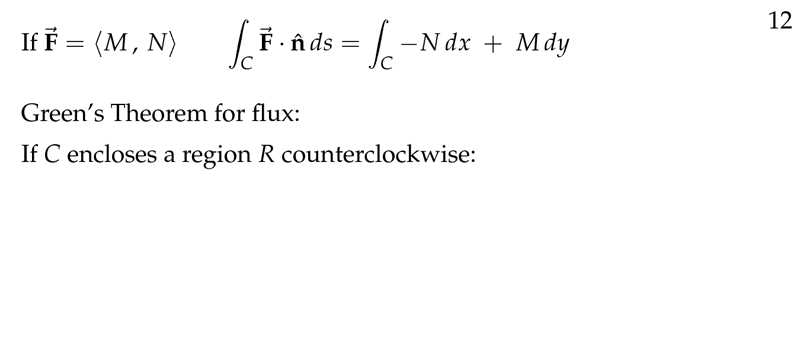
Figure 1: What is the Green’s Theorem for flux
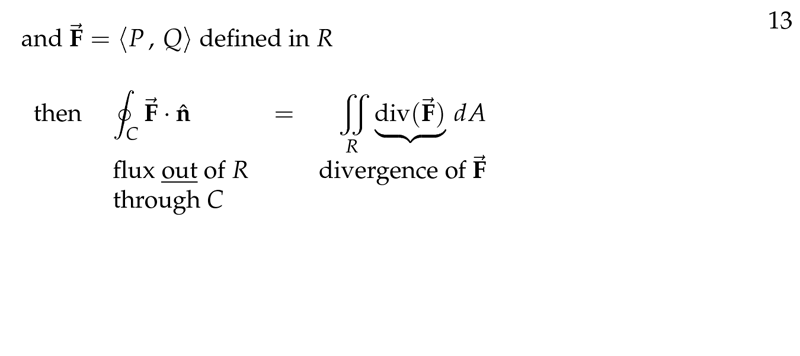
Figure 2: Green’s Theorem for flux

Figure 3: Green’s Theorem in normal form vs tangential form
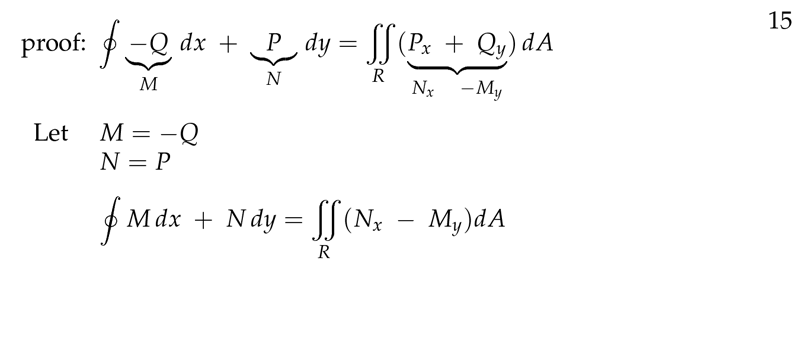
Figure 4: Proof of Green’s Theorem for flux
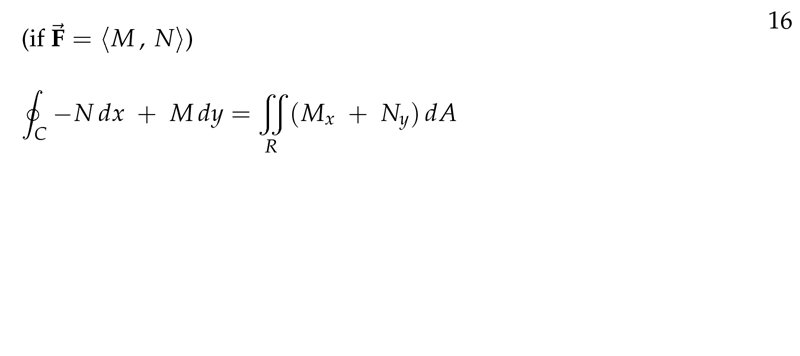
Figure 5: Changing name of \(\vb{F}\) components
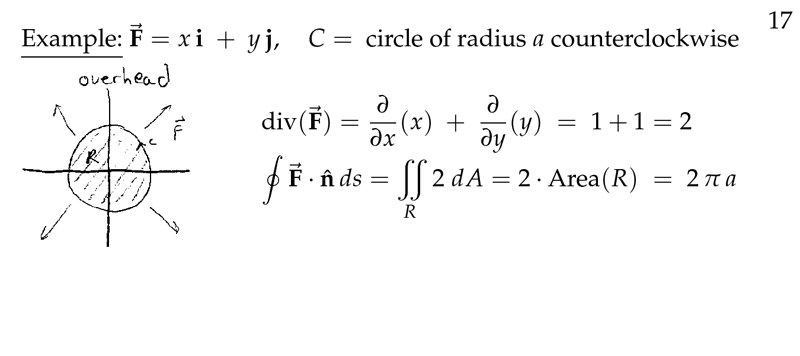
Figure 6: Example of Green’s Theorem for flux
2 Explain why flux is a line integral
2.1 Front
Explain why flux is a line integral
Let \(\vb{F}\) a vector field, and \(C\) any curve
2.2 Back
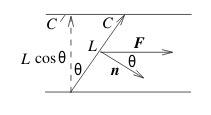
We can divide up the curve \(C\) and apply to each of the approximating line segments, so:
mass-transport rate across \(k\text{-th}\) line segment \(\approx (\vb{F_k} \cdot \vu{n_k}) \Delta s_{k}\)
Add up all these subdivision and \(\Delta s \to 0\)
mass-transport rate across \({\displaystyle C = \int_C \vb{F} \cdot \vb{n} \dd{s}}\)
So, this line integral is called flux of \(\vb{F}\) across \(C\)
3 How can you write \(\vu{n}\dd{s}\) as vector?
3.1 Front
How can you write $\vu{n}\dd{s}$ as vector?
Write in terms of components, similarly to \(\dd{\vb{r}} = \ev{\dd{x}, \dd{y}}\)
3.2 Back
\(\vu{n}\) is 90 degrees clockwise to tangent vector \(\vb{T}\). As you can write \(\vb{T} \dd{s}\)
\(\dd{\vb{r}} = \vb{T} \dd{s} = \ev{\frac{\dd{x}}{\dd{s}}, \frac{\dd{y}}{\dd{s}}} \dd{s} = \ev{\dd{x}, \dd{y}}\)
Clockwise this vector 90 degrees
\(\vu{n} \dd{s} = \ev{\frac{\dd{y}}{\dd{s}}, - \frac{\dd{x}}{\dd{s}}} \dd{s} = \ev{\dd{y}, - \dd{x}}\)
4 What is the Green’s Theorem for flux?
4.1 Front
What is the Green’s Theorem for flux?
Let \(\vb{F} = \ev{M,N}\) a 2 dimensional flow field, and \(C\) a simple closed curve, positively oriented
4.2 Back
- Flux of \(\vb{F}\) across \(C\) \({\displaystyle = \oint_C M \dd{y} - N \dd{x}}\)
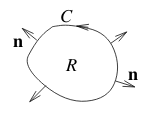
As \(\vu{n}\) points outwards, away from \(R\), the flux is positive where the flow is out of \(R\), flow into \(R\) counts as negative flux
Applying Green’s Theorem to the line integral
\({\displaystyle \oint_C M \dd{y} - N \dd{x} = \oint_C - N \dd{x} + M \dd{y} = \iint_R (M_x - (- N_y)) \dd{A} = \iint_R (M_x + N_y) \dd{A}}\)
5 How is the flow if the flux of \(\vb{F}\) across \(C\) is positive?
5.1 Front
How is the flow if the flux of $\vb{F}$ across $C$ is positive?
Let \(\vb{F} = \ev{M,N}\) a 2 dimensional flow field, and \(C\) a simple closed curve, positively oriented
5.2 Back
It’s away from \(R\)
As \(\vu{n}\) points outwards, away from \(R\), the flux is positive where the flow is out of \(R\), flow into \(R\) counts as negative flux
6 What is the two-dimensional divergence of \(\vb{F}\)
6.1 Front
What is the two-dimensional divergence of $\vb{F}$
Let \(\vb{F} = \ev{M,N}\)
6.2 Back
\({\displaystyle \text{div} \vb{F} = M_x + N_y}\)
It’s a scalar function of two variables
7 Which is the physical interpretation of \(\text{div} \vb{F}\)?
7.1 Front
Which is the physical interpretation of $\text{div} \vb{F}$?
Let \(\vb{F}\) a flow field continuously differentiable
7.2 Back
If \(\vb{F}\) is continuously differentiable, then \(\text{div} \vb{F}\) is a continuous function. Looking at a small rectangle, the flux of \(\vb{F}\) across the sides of this rectangle is constant
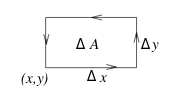
For \({\displaystyle \iint_R \text{div} \vb{F} \dd{A}}\) is the flux across sides of rectangle
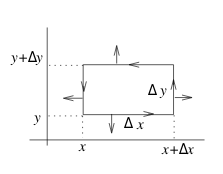
Calculating the flux over each side
- Flux across top: \(\approx (\vb{F}(x, y + \Delta y) \cdot \vu{j}) \Delta x = N(x,y+\Delta y) \Delta x\)
- Flux across bottom: \(\approx (\vb{F}(x, y) \cdot - \vu{j}) \Delta x = - N(x,y) \Delta x\)
- Adding up (top and bottom):
- \({\displaystyle \approx (N(x,y + \Delta y) - N(x,y)) \Delta x \approx \biggl(\pdv{N}{y} \Delta y \biggr) \Delta x}\)
- Similarly for left and right
- \({\displaystyle \approx (M(x + \Delta x,y) - M(x,y)) \Delta y \approx \biggl(\pdv{N}{x} \Delta x \biggr) \Delta y}\)
- Adding up all sides
- \({\displaystyle \approx \biggl(\pdv{M}{x} + \pdv{N}{y} \biggr) \Delta x \Delta y}\)
If the total flux over the sides of the small rectangle is positive, this means that there is a net flow out of the rectangle. For example, if there is a source adding fluid directly to the rectangle, as pouring water in the rectangle (According to conservation of matter).
If the total flux is negative, there is a net flow into the rectangle. So this implies there is a sink withdrawing fluid from the rectangle. (Negative source)
The source rate for the rectangle is the flux over sides of rectangle, so we can say that
- \({\displaystyle \text{source rate for the rectangle} = \biggl(\pdv{M}{x} + \pdv{N}{y} \biggr) \Delta A}\)
- \({\displaystyle \text{source rate at }(x,y) = \biggl(\pdv{M}{x} + \pdv{N}{y} \biggr) = \text{div} \vb{F}}\)
- \({\displaystyle \text{source rate for }R = \iint_R \text{div} \vb{F} \dd{A}}\)
8 How can interpret physically Green’s Theorem in the normal form?
8.1 Front
How can interpret physically Green’s Theorem in the normal form?
8.2 Back
\begin{align*} \qq{total flux across} C &= \qq{source rate for} R \\\ \oint_C M \dd{y} - N \dd{x} &= \iint_R \biggl(\pdv{M}{x} + \pdv{N}{y} \biggr) \dd{A} \end{align*}
9 What is the work by \(\vb{F}\) around \(C\)
9.1 Front
What is the work by $\vb{F}$ around $C$
Let \(\vb{F}\) a two dimensional vector field and \(C\) any curve
9.2 Back
\({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = \oint_C M \dd{x} + N \dd{y}}\)
10 What is the source rate for \(R\)
10.1 Front
What is the source rate for $R$
Let \(R\) be a region closed by a curve \(C\), and \(\vb{F}\) a two dimensional vector field
10.2 Back
Source rate for \(R\) is \({\displaystyle \iint_R \text{div} \vb{F} \dd{A}}\)
Using the Green’s Theorem in the vector form, the flux of \(\vb{F}\) across \(C\) is the source rate for \(R\)
\({\displaystyle \oint_C \vb{F} \vu{n} \dd{s} = \int_R \text{div} \vb{F} \dd{A}}\)
11 Compute the flux of \(\vb{F}\) across \(C\) using geometric methods
11.1 Front
Compute the flux of $\vb{F}$ across $C$ using geometric methods
Let \(\vb{F} = g( r) \ev{x,y}\), where \(g( r)\) is a function of the radial distance \(r\). \(C\) is the circle of radius \(a\) centered at the origin and traversed in a clockwise direction
11.2 Back
\(\vb{F}\) is a radial field, and \(\vu{n}\) is parallel in the opposite direction, so we have \(\vb{F} \vu{n} = -g(a) \cdot a\) at the circle.
Flux = \(\int_0^{2 \pi} -g(a)a \dd{s} = -g(a) 2 \pi a^2\)
12 Is this vector field conservative
12.1 Front
Is this vector field conservative
Let \(\vb{F} = r^n \ev{x,y}\) for any \(n\) integer
12.2 Back
This is radial vector field, as \(r^n = (x^2 + y^2)^{n/2}\) is not defined at the origin when \(n<0\)
\(\vb{F} = \ev{M,N}\), of all values of \((x,y)\) except the origin and \(n=0\), you can apply Green’s Theorem directly.
As \({\displaystyle M_y = N_x = n r^{n-2}xy}\), so \(\text{curl} \vb{F} = 0\)
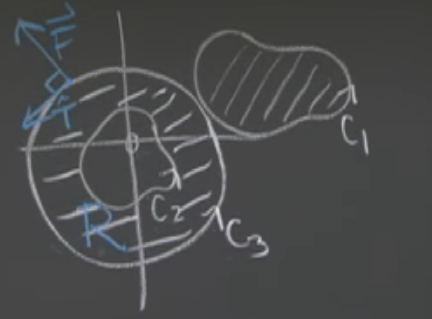
Using extended Green’s Theorem,
- \({\displaystyle \oint_{C_1} \vb{F} \dd{\vb{r}} = 0}\)
- \({\displaystyle \oint_{C_3} \vb{F} \dd{\vb{r}} = 0}\) (it’s a circle)
Any region between \(C_3\) and \(C_2\), the \(\iint_R \text{curl} \vb{F} = 0\), so this vector field is conservative
13 Where can we say the \(\vb{F}\) is conservative?
13.1 Front
Where can we say the F is conservative?
Let \({\displaystyle \vb{F} = \frac{-y \vu{i} + x \vu{j}}{x^2 + y^2}}\)
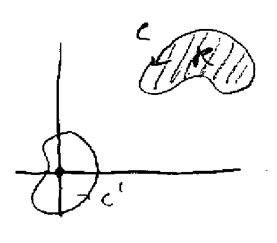
What happens at point \(0,0\)?
13.2 Back
\(\vb{F}\) is not defined at origin, but \(\text{curl} \vb{F} = 0\) everywhere else
Domain is the plane less origin: not simply connected
At \(C’\) can’t use Green’s Theorem directly, so we need to use an expansion of this theorem.
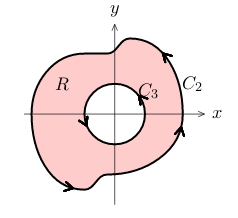
Where in the region inside \(C_2\) and \(C_3\), \({\displaystyle \iint_R \text{curl} \vb{F} \dd{A} = 0 = \oint_{C_2} \vb{F} \cdot \dd{\vb{r}} - \oint_{C_3} \vb{F} \cdot \dd{\vb{r}}}\)
This implies that \({\displaystyle \oint_{C_2} \vb{F} \cdot \dd{\vb{r}} = \oint_{C_3} \vb{F} \cdot \dd{\vb{r}}}\).
As \(C_3\) is a circle, we can compute this line integral geometrically.
\({\displaystyle \vb{F} \cdot \vu{T} = 1/a \implies \oint_{C_3} \vb{F} \cdot \dd{\vb{r}} = \int_{C_3} \frac{1}{a} \dd{s} = \frac{2 \pi a}{a} = 2 \pi}\)