1 Chalkboard

Figure 1: Flux presentation
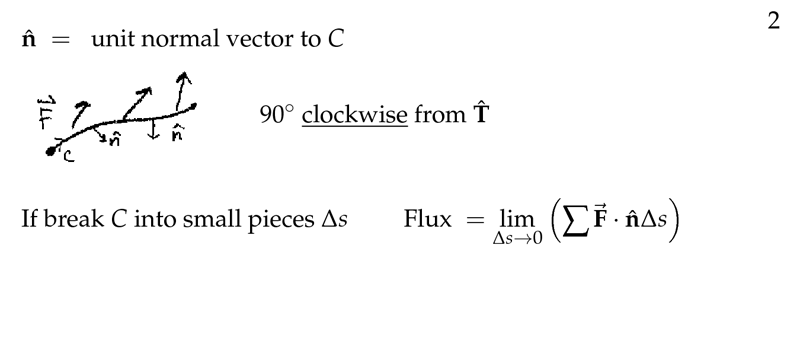
Figure 2: \(\vu{n}\) as clockwise from \(\vu{T}\)
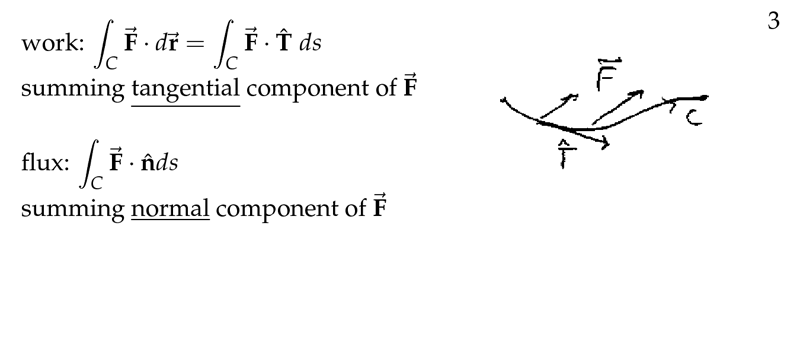
Figure 3: Flux and Work comparison

Figure 4: Intepretation of Flux
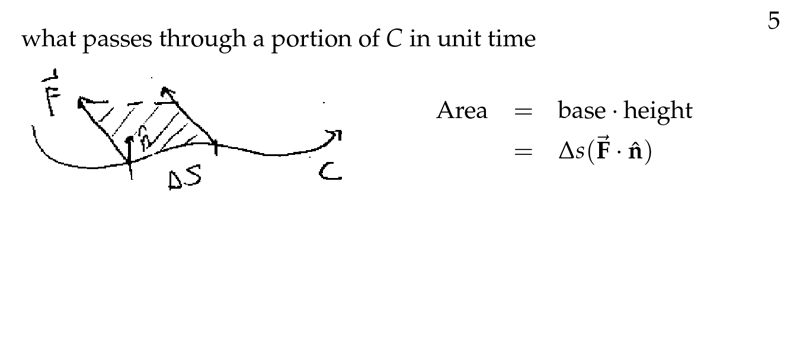
Figure 5: Visualization of Flux
Figure 6: What flows across \(C\)
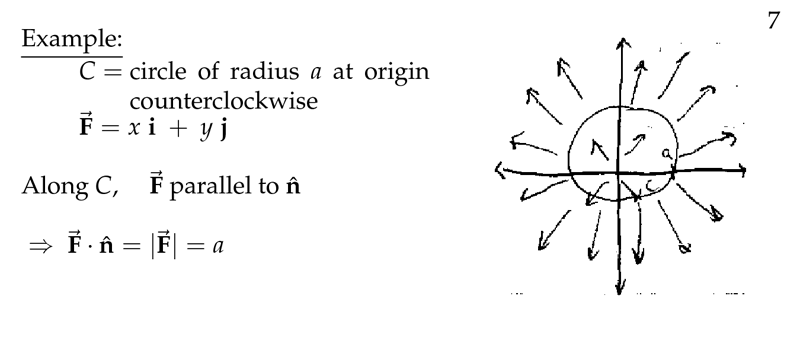
Figure 7: Example of Flux
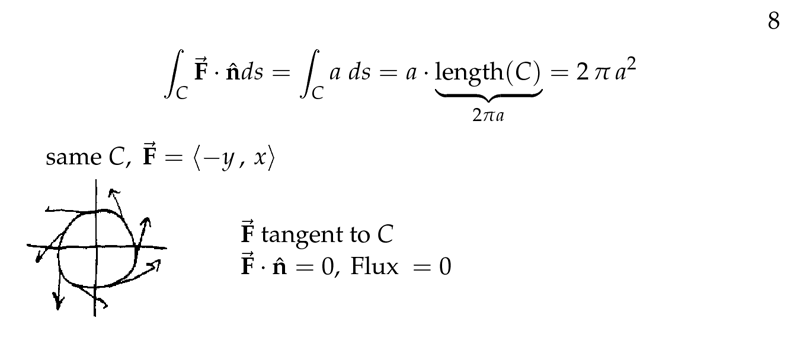
Figure 8: Example of Flux II

Figure 9: Calculation flux using components
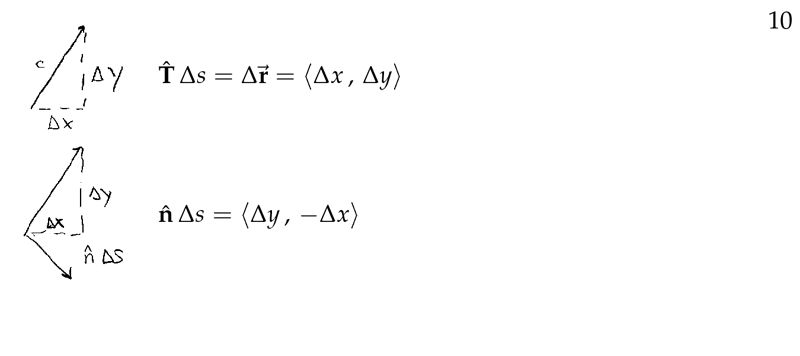
Figure 10: \(\vu{T}\) vs \(\vu{n}\)
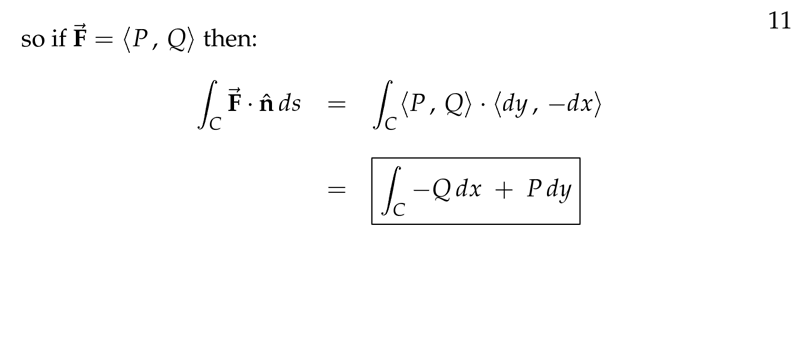
Figure 11: Line integral for Flux
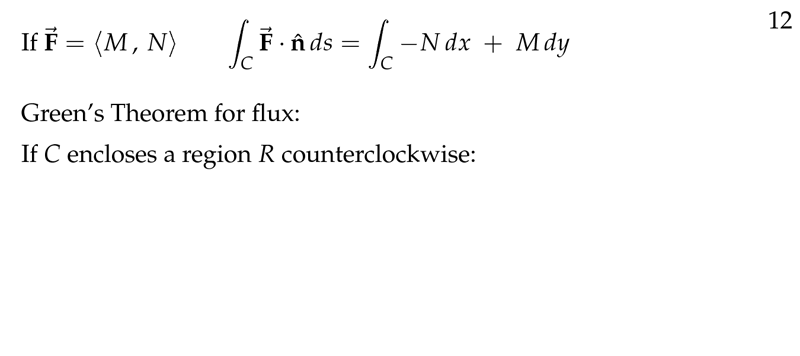
Figure 12: Another way of writing flux components
2 Find \(M\) and \(N\) equals the polar moment of inertia
2.1 Front
Find $M$ and $N$ equals the polar moment of inertia
- \({\displaystyle \oint_C M \dd{x} + N \dd{y}}\)
- Density: uniform
- Region in the plane boundary \(C\)
2.2 Back
- Let \(R\) be the region enclosed by \(C\) and \(\phi\) be the uniform density of \(R\)
- Polar moment of inertia: \({\displaystyle \iint_R \dd{I} = \iint_R r^2 \dd{m} = \iint_R (x^2 + y^2) \phi \dd{A}}\)
Using the Green’s Theorem, we need that \(N_x - M_y = \delta x^2 + \delta y^2\). Choosing the simplest choice \(N_x = \delta y^2\) and \(M_y = -\delta x^2\). So, this leads to \(N = \delta xy^2\) and \(M = -\delta yx^2\)
\({\displaystyle \oint_C -\delta x^2 y \dd{x} + \delta x y^2 \dd{y}}\)
3 What is a flux?
3.1 Front
What is a flux?
Let \(\vb{F}\) be a vector field and \(C\) a path
3.2 Back
It’s another line integral, it’s called Flux of \(\vb{F}\) across \(C\)
\({\displaystyle \int_C \vb{F} \cdot \vu{n} \dd{s}}\)
4 How can we get the normal vector to a path \(C\)
4.1 Front
How can we get the normal vector to a path $C$
Let \(C = r(t)\)
4.2 Back
\(\vu{n}\) is \(90\) degrees clockwise from \(\vu{T}\)
\(\Delta \vb{r} = \ev{\Delta x, \Delta y} = \vu{T} \Delta s\)
\(\vu{n} \Delta s = \ev{\Delta y, - \Delta x}\)
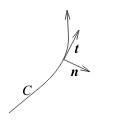
This direction is opposite to the one customarily used in kinematics where \(\vb{t}\) and \(\vb{n}\) form a right-handed coordinate system for motion along \(C\)
5 What is the interpretation of Flux of \(\vb{F}\) (Velocity field)
5.1 Front
What is the interpretation of Flux of $\vb{F}$ (Velocity field)
Across curve \(C\), two-dimensional flow field
5.2 Back
Flux measures how much fluid passes through curve \(C\) per unit time

6 What is the equation of flux \(\vb{F}\) across \(C\)?
6.1 Front
What is the equation of flux $\vb{F}$ across $C$?
In symbols and notation of differentials. Where \(x(t)\), \(y(t)\) is any parametrization of \(C\)
6.2 Back
\(\vu{n} \dd{s} = \dd{y} \vu{i} - \dd{x} \vu{j}\)
\({\displaystyle \int_C \vb{F} \cdot \vu{n} \dd{s} = \int_C M \dd{y} - N \dd{x} = \int_C \biggl( M \dv{y}{t} - N \dv{x}{t} \biggr) \dd{t}}\)
7 Which is the natural physics interpretation for flux?
7.1 Front
Which is the natural physics interpretation for flux?
Where \(\vb{F}\) as representing a two-dimensional flow field
7.2 Back
The line integral represents the rate with respect to time at which mass is being transported across \(C\)
8 Which is the convention for positive and negative flux
8.1 Front
Which is the convention for positive and negative flux
\(\vb{F}\) is two-dimensional flow field
8.2 Back
If we think of the flow as taking place in a shallow tank of unit depth. The convention about \(\vb{n}\) makes this mass-transport rate positive if the flow is from left to right as you face in the positive direction of \(C\), and negative in the other case
9 How can we express the mass-transport rate across \(C\) in a vector field \(\vb{F}\)?
9.1 Front
How can we express the mass-transport rate across \(C\) in a vector field \(\vb{F}\)?
Let \(\vb{F}\) a constant vector field representing a flow, and \(C\) is a directed line segment of length \(L\)
9.2 Back
How can we express the mass-transport rate across \(C\) in a vector field \(\vb{F}\)?
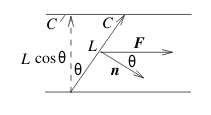
Using \(C’\), mass-transport rate across \({\displaystyle C’ = \abs{\vb{F}} (L \cos \theta) = (\vb{F} \cdot \vu{n}) L}\)