1 Chalkboard
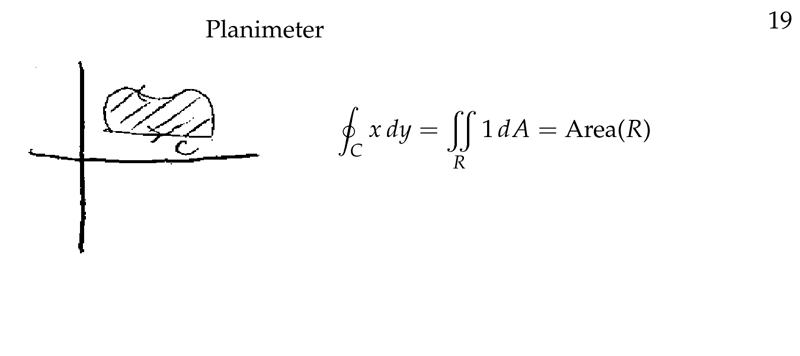
Figure 1: Planimeter
2 What is a planimeter?
2.1 Front
What is a planimeter?
Define it, and write its equation
2.2 Back
It’s an instruments for measuring areas through closing perimeters. This instruments uses the Green’s Theorem, and the equation
\({\displaystyle \oint_C x dy = \iint_R \dd{A}}\)
3 How can you use line integrals for computing areas?
3.1 Front
How can you use line integrals for computing areas?
Compute the equation
3.2 Back
- The area is \({\displaystyle \iint_R \dd{A}}\)
- Using Green’s Theorem, you can set a relationship between line integrals and double integral
If, \({\displaystyle \iint_R N_x - M_y \dd{A}}\) you can convert this double integral for computing area if \(N_x = 1\) or \(M_y = -1\). So line integral is
- If \(N_x = 1\), \(0 \dd{x} + x \dd{y}\)
- If \(M_y = -1\), \(-y \dd{x} + 0 \dd{y}\)
So, for computing the area you can set any of these
- \({\displaystyle \oint_C x \dd{y}}\)
- \({\displaystyle \oint_C -y \dd{x}}\)
4 What does mean a curve oriented positively around the region it encloses?
4.1 Front
What does mean a curve oriented positively around the region it encloses?
4.2 Back
A smooth closed counterclockwise curve