1 Chalkboard
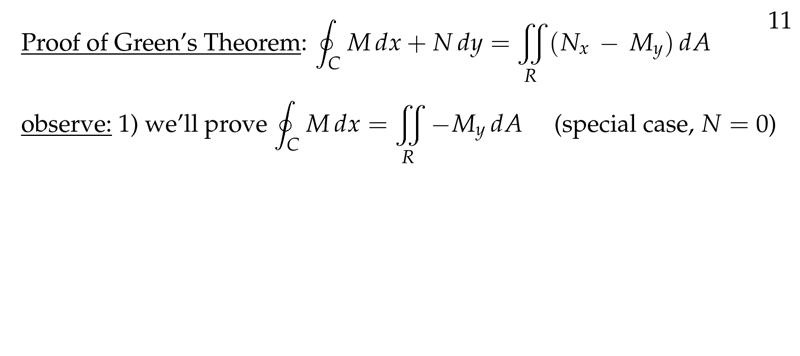
Figure 1: Proof of Green’s Theorem

Figure 2: 2 observations
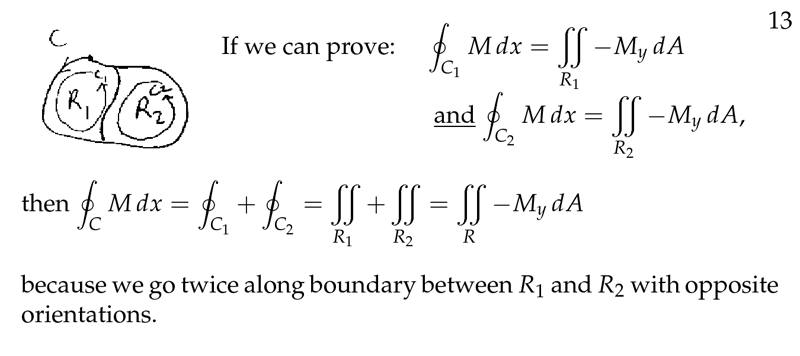
Figure 3: Proof of one part
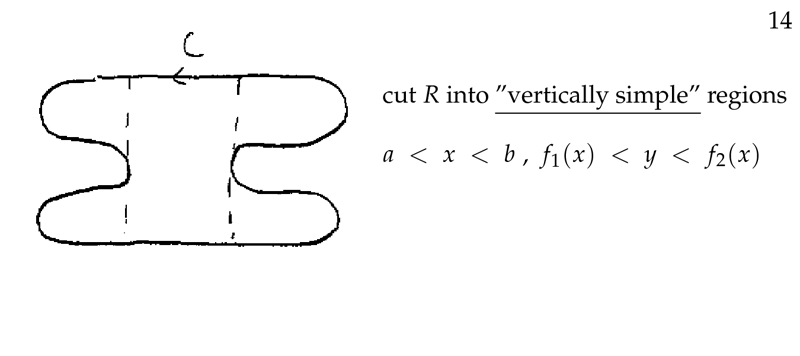
Figure 4: Cut (R) “vertically simple”
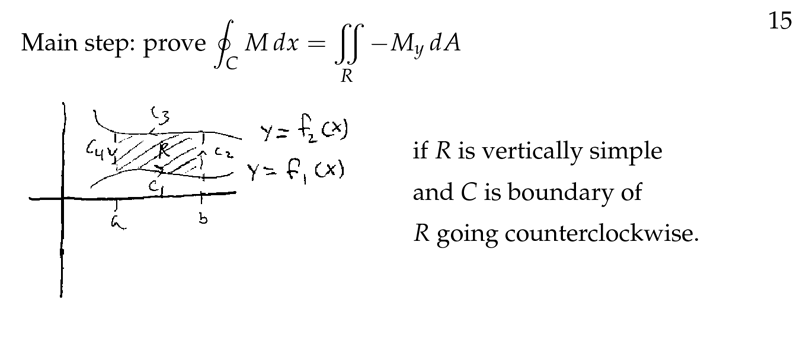
Figure 5: Main step of prove
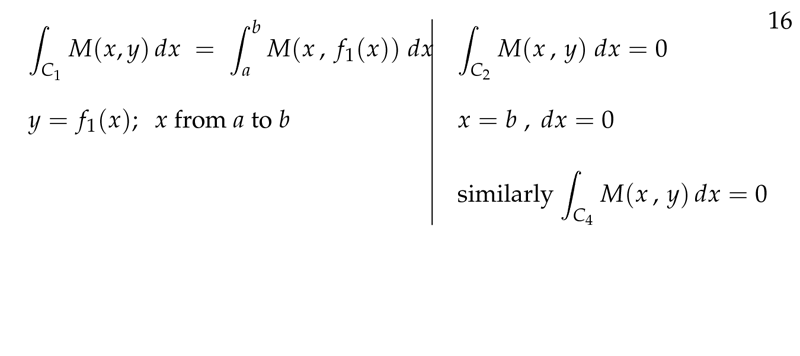
Figure 6: Line integrals
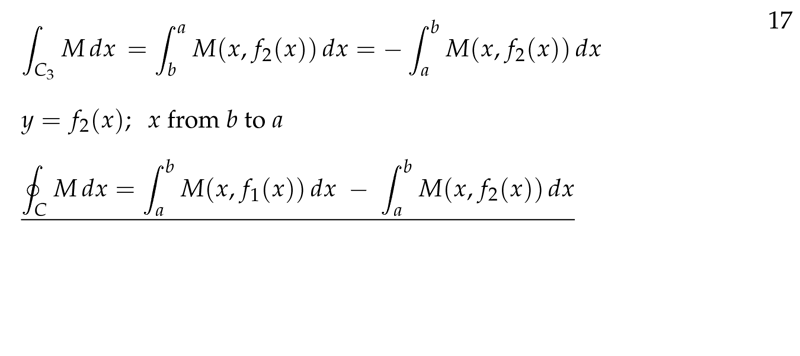
Figure 7: Sum of all line integrals
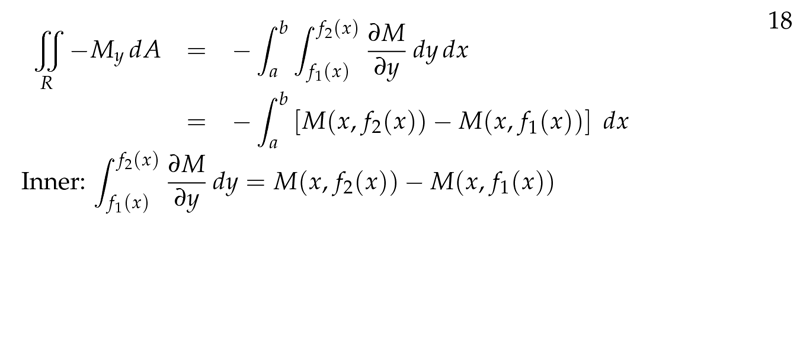
Figure 8: Doble integral of internal region
2 Which step we need to do for proofing Green’s Theorem?
2.1 Front
Which step we need to do for proofing Green’s Theorem?
Only describe the steps
2.2 Back
Green’s Theorem: \({\displaystyle \oint_C M \dd{x} + N \dd{y} = \iint_R (N_x - M_y) \dd{A}}\)
First Observation
- Separate this integral as \(N = 0\) and \(M = 0\)
- \({\displaystyle \oint_C M \dd{x} = \iint_R - M_y \dd{A}}\)
- \({\displaystyle \oint_C N \dd{y} = \iint_R N_x \dd{A}}\)
- The sum of both equation is the complete proof of Green Theorem
- Separate this integral as \(N = 0\) and \(M = 0\)
Second Observation
- Decompose \(R\) into simpler regions, creating new paths around this new regions. The sums of the regions is \(R\) and the sum of \(C_i\) path around each region is \(C\) (this is true, because all path are counterclockwise, and 2 path in the boundaries with opposite orientations is \(0\)).
- You can use “vertically simple”, “horizontal simple” or
rectangles
Main Step (using the separated integral)
- Calculate the right hand side of Green’s Theorem
- Set the outer integral
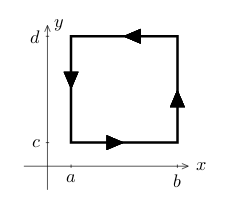
- Calculate the left hand side of Green’s T
- Along some size the integral is \(0\)
- \({\displaystyle \int_a^b M(x,c) - M(x,d) \dd{x}}\)
- Calculate the right hand side of Green’s Theorem
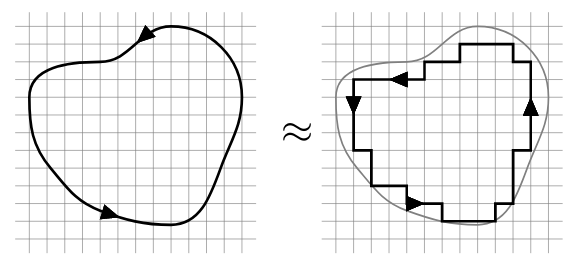
Any region can be approximated as closely as we want by a sum of rectangles, Green’s Theorem must hold on arbitrary regions