1 Chalkboard

Figure 1: Special case of Green Theorem
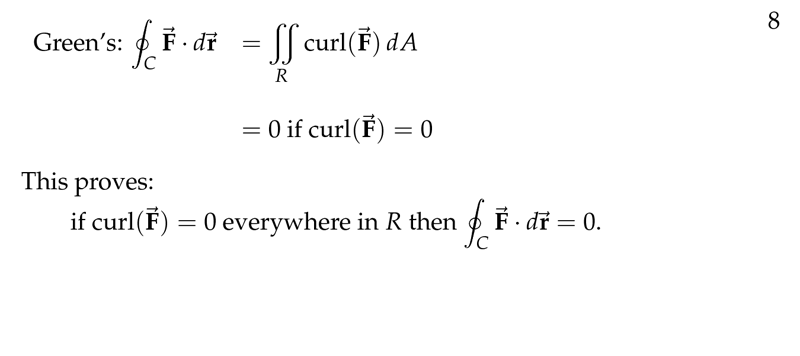
Figure 2: Proof of \(\vb{F}\) conservative when curl \(\vb{F}\) is \(0\)
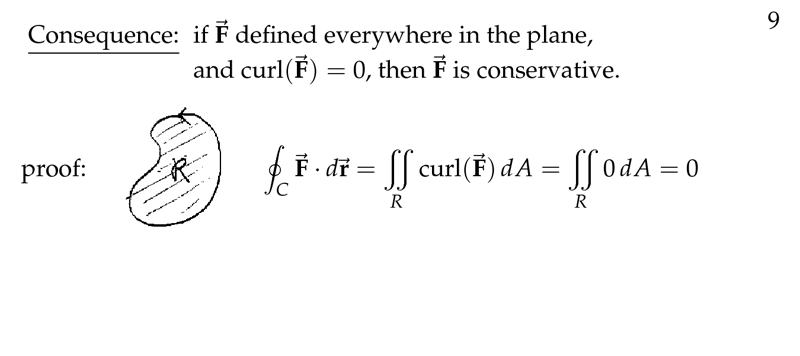
Figure 3: Consequence of \(\text{curl} \vb{F} = 0\)

Figure 4: Cannot Green theorem when \(\vb{F}\) is not defined at point inside the region
2 Why if \(\text{curl} \vb{F} = 0\) implies \(\vb{F}\) is conservative
2.1 Front
Why if $\text{curl} \vb{F} = 0$ implies $\vb{F}$ is conservative
\(\vb{F}\), and \(C\) is a closed path
2.2 Back
\(\vb{F}\) must be defined and differentiable everywhere
Because of Green’s Theorem
\({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = \iint_R \text{curl} \vb{F} \dd{A}}\)
If \({\displaystyle \text{curl} \vb{F} = 0 \implies \iint_R 0 \dd{A} = 0}\), so \({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = 0} \implies \vb{F}\) is conservative
Be careful with non conservative field with \(\text{curl} \vb{F} = 0\), you need to check the requirement that \(\vb{F}\) is defined and differentiable everywhere.