1 Chalkboard
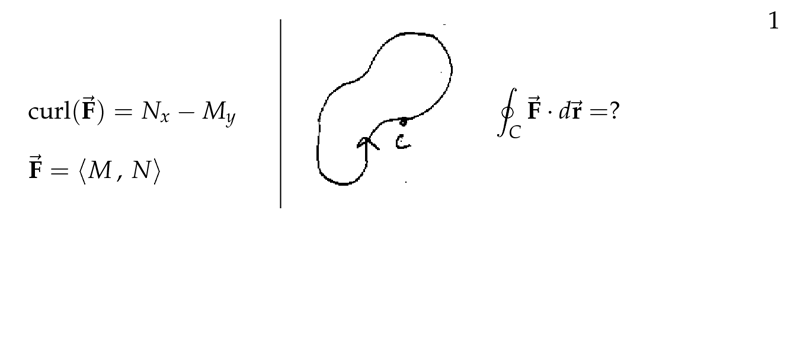
Figure 1: Line integral for closed path

Figure 2: Green’s Theorem
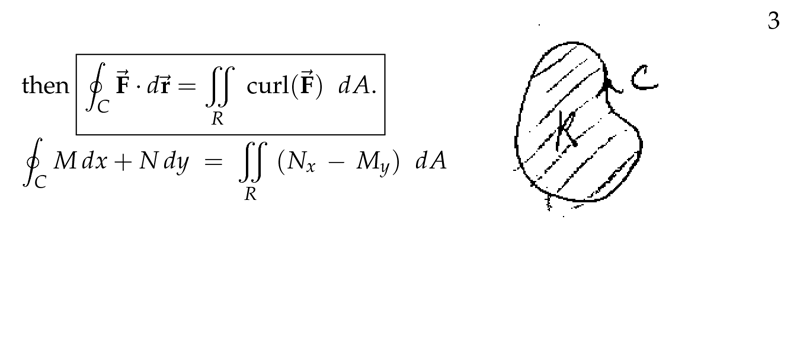
Figure 3: Green’s Theorem (II)
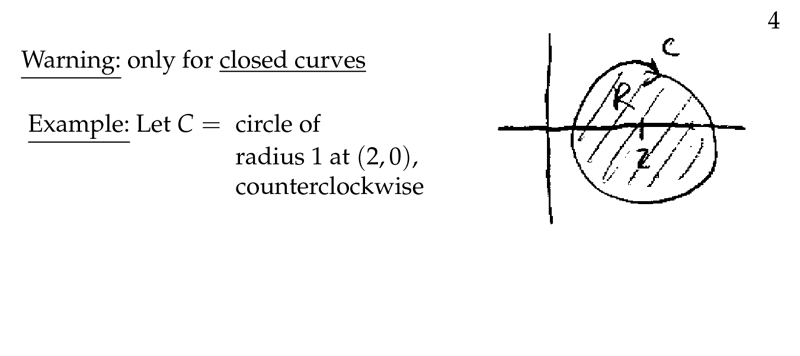
Figure 4: Warning and example
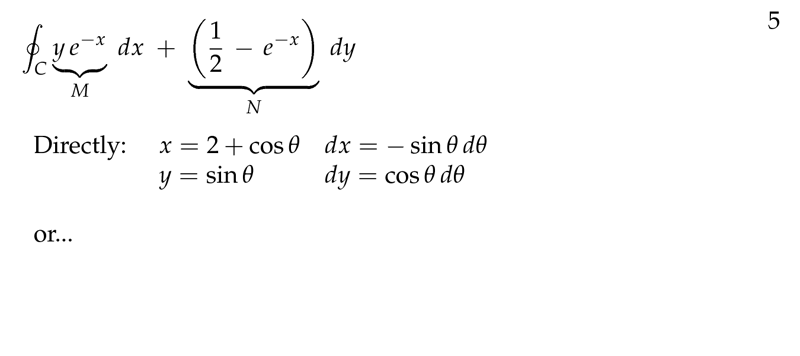
Figure 5: Computing directly
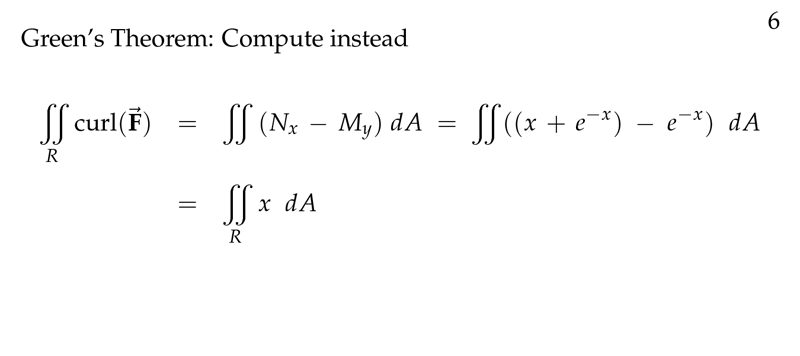
Figure 6: Using Green’s Theorem

Figure 7: Solving with geometry and simmetry
2 Describe geometrically how is this vector field?
2.1 Front
Describe geometrically how is this vector field?
\(\vb{F} = \frac{y \vu{i} - x \vu{j}}{r}\)
2.2 Back
Vector a \(P\) has unit length, and the clockwise direction perpendicular to \(OP\)
3 Write the vector fields that describe…
3.1 Front
Write the vector fields that describe…
The vector at \((x,y)\) is directed radially in towards the origin, with magnitude \(r^2\)
3.2 Back
Vector: \(\vb{v} = \ev{-x, -y}\), that \(\vu{v} = \ev{-x/r, -y/r}\)
So: \(r^2 \vu{v} = -r \ev{x,y}\)
4 Write the vector fields that describe…
4.1 Front
Write the vector fields that describe…
The vector at \((x,y)\) is tangent to the circle through \((x,y)\) with center at the origin, clockwise direction, magnitude \(1/r^2\)
4.2 Back
- Vector at \((x,y)\) that set the direction of the field
- \(\vb{v} = \ev{y, -x}\), \(\vu{v} = \ev{y/r, -x/r}\)
- With magnitude \(1/r^2\)
- \(\vb{F} = \ev{y/r^3, -x/r^3}\)
5 What are the conditions to use Green’s Theorem
5.1 Front
What are the conditions to use Green’s Theorem
5.2 Back
- \(C\) is a simple closed curve (simple means it never intersects itself)
- \(R\) the interior of \(C\)
- Counterclockwise: \(C\) must be positively oriented, that is, it must be traversed so its interior is on the left as you move in around the curve
- \(C\) is piecewise smooth
- \(\vb{F}\) must be defined and differentiable for all \((x,y)\) on the region
6 What is the Green’s Theorem
6.1 Front
What is the Green’s Theorem
Write the theorem, let \(C\) be a curve, and \(\vb{F}\) a vector field
6.2 Back
- \(C\) is simple closed curve, counterclockwise and piecewise smooth
- \(\vb{F} = \ev{M, N}\) is a vector field, and it’s defined for all \((x,y)\) of the region inside of curve
\({\displaystyle \oint_C M \dd{x} + N \dd{y} = \iint_R N_x - M_y \dd{A}}\)
We call \(N_x - M_y\) the two dimensional curl \(\text{curl} \vb{F}\)
\({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = \iint_R \text{curl} \vb{F} \dd{A}}\)
7 Can I apply Green’s Theorem on this \(\vb{F}\)?
7.1 Front
Can I apply Green’s Theorem on this $\vb{F}$?
\({\displaystyle \vb{F} = \frac{-y \vu{i} + x \vu{j}}{x^2 + y^2}}\)
\(C\) is a unit circle from the origin
7.2 Back
No, you cannot apply Green Theorem because \(\vb{F}\) is not defined for the origin, so the \(\text{curl} \vb{F}\) is not defined neither.
\(\vb{F}\) could be conservative for any other points, but if the region inside of the closed path contains point where \(\vb{F}\) are not defined, the \(\text{curl} \vb{F}\) is not defined neither.