1 Chalkboard

Figure 1: Recall \(\vb{F}\) using curl
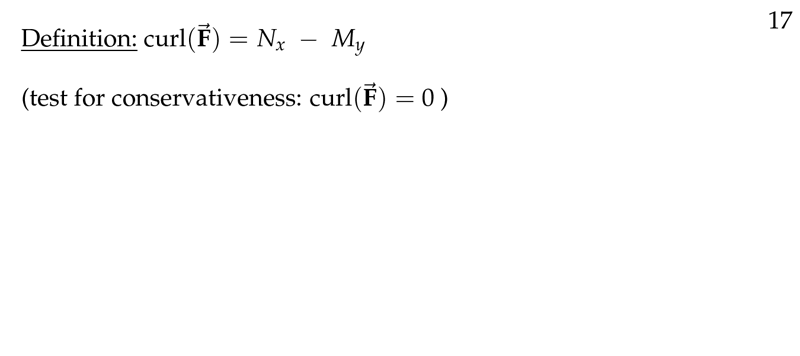
Figure 2: Definition of curl

Figure 3: Curl for velocity field
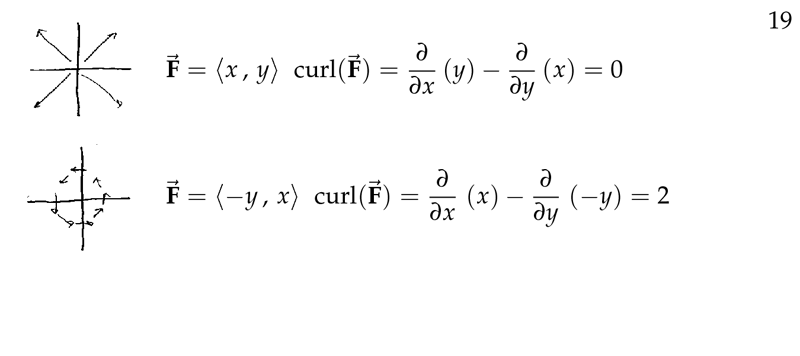
Figure 4: Examples of curl

Figure 5: What measure the curl
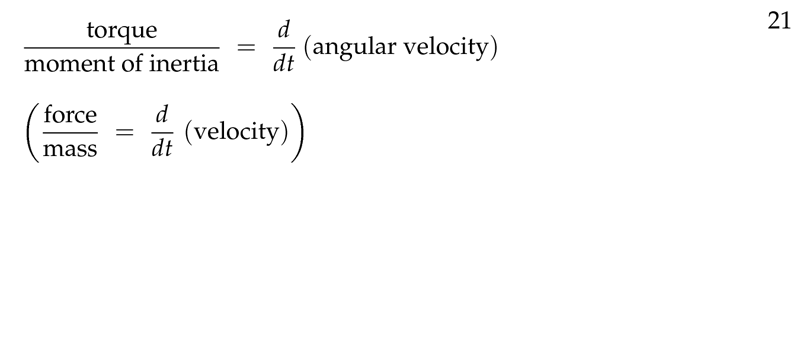
Figure 6: Physics derivative measures
2 What measures the curl in a velocity field?
2.1 Front
What measures the curl in a velocity field?
2.2 Back
Curl measures (2x) angular velocity of rotational component of a velocity field
3 What measure the curl in a force field?
3.1 Front
What measure the curl in a force field?
3.2 Back
Torque exerted on a test object on each point
4 How can we parametrize the circular movement with constant angular velocity \(\omega\)
4.1 Front
How can we parametrize the circular movement with constant angular velocity \(\omega\)
No radial velocity (position vector of a circle)
4.2 Back
How can we parametrize the circular movement with constant angular velocity \(\omega\)
- \(r = r_0\)
- \(\theta = \theta_0 + \omega t\)
In polar coordinates: \((x(t), y(t)) = (r_0 \cos (\theta_0 + \omega t), r_0 \sin(\theta_0 + \omega t))\)