1 Chalkboard

Figure 1: Finding the potential
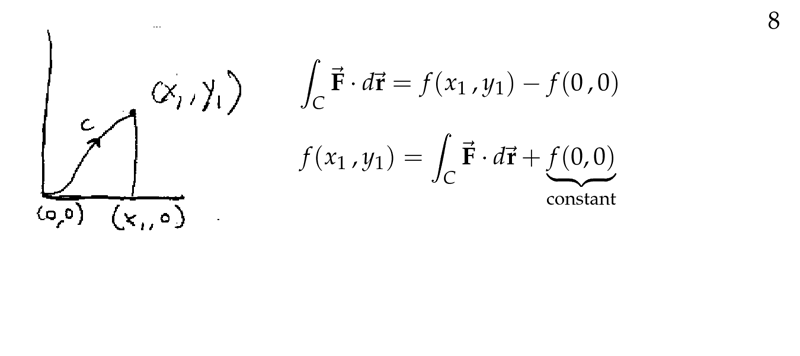
Figure 2: Choosing a path
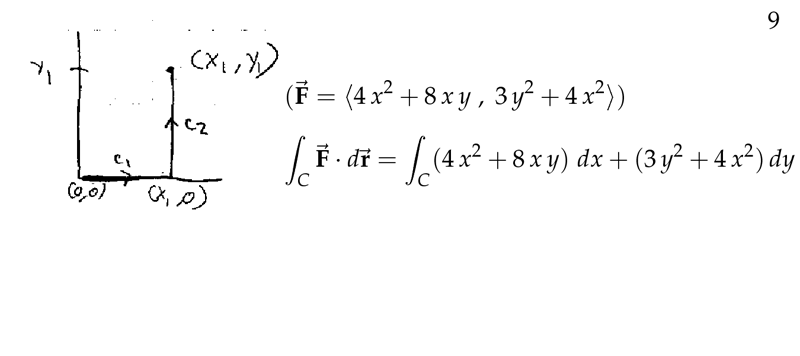
Figure 3: Choosing a easiest path
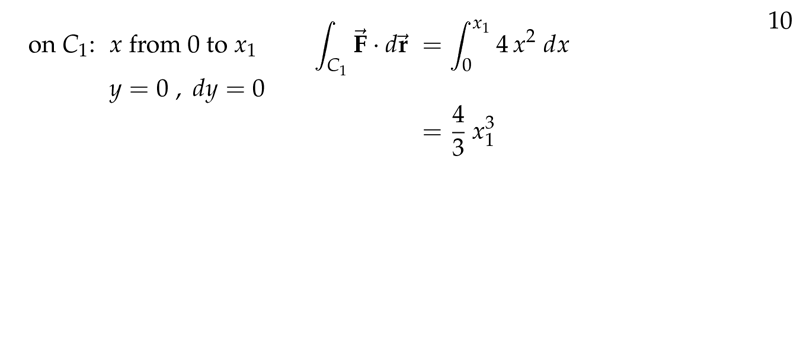
Figure 4: Path \(C_{1}\)
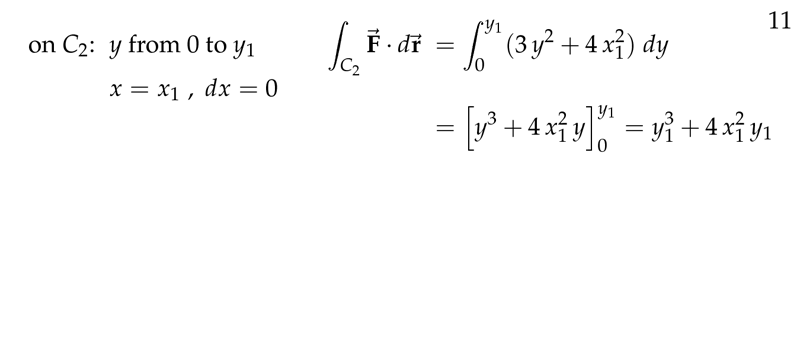
Figure 5: Path \(C_{2}\)
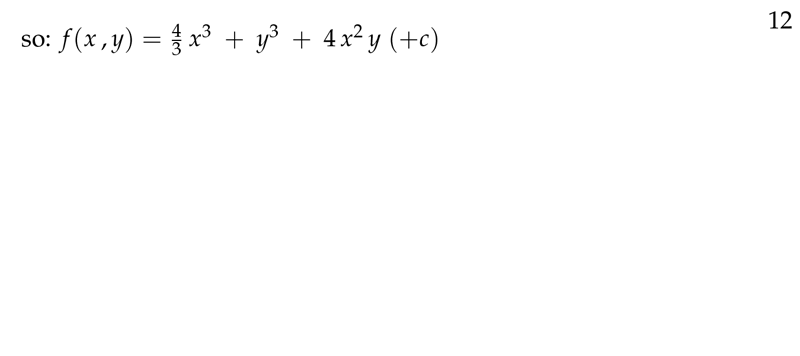
Figure 6: The potential function
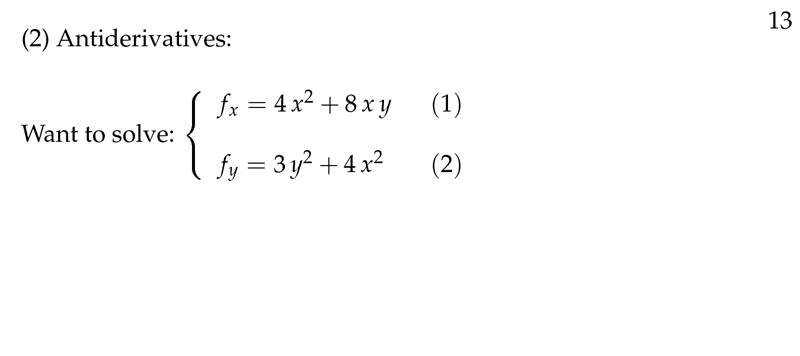
Figure 7: Using antiderivatives
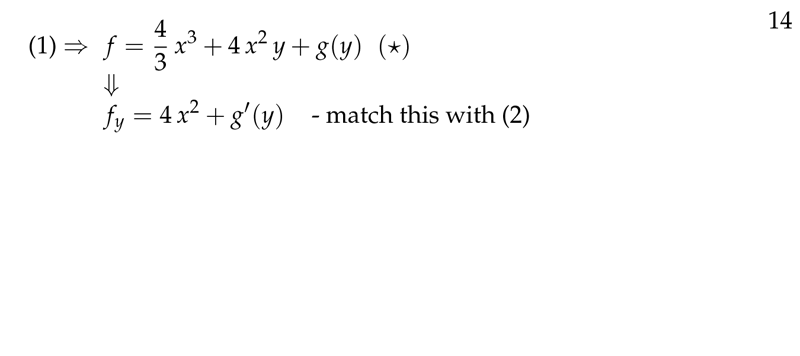
Figure 8: First using one part, and \(f(y)\) as constant function
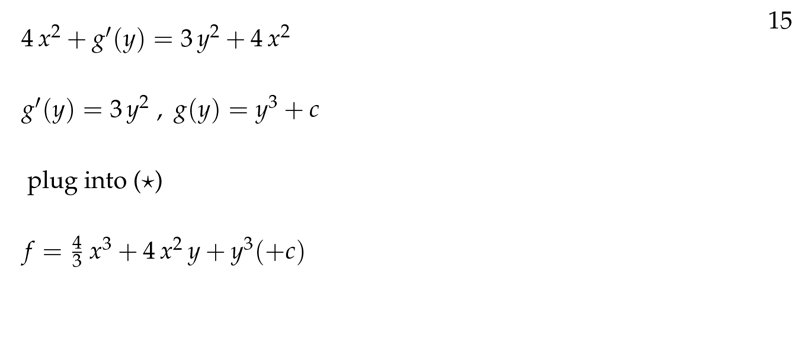
Figure 9: Getting potential function

Figure 10: Only method valid for gradient field
2 Which path can we choose to find potential function?
2.1 Front
Which path can we choose to find potential function?
Given \(\vb{F}\) choose any path to get the potential function
2.2 Back
- \(\vb{F} = \grad{f}\)
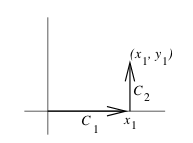
- You can get any path, but easiest start at origin \((0,0)\) and finish at \((x_1,y_1)\)
- And you divide in 2 path
- \(C_1\) along \(x\text{-axis}\)
- \(C_2\) along \(x=x_1\)
3 Why the physics potential function use the negative sign?
3.1 Front
Why the physics potential function use the negative sign?
3.2 Back
The negative sign is used by physicist so that the potential difference will represent work done against the field \(\vb{F}\), rather than work done by the field, as the convention is in mathematics
4 How can you get the potential function using FTC for Line Integrals?
4.1 Front
How can you get the potential function using FTC for Line Integrals?
\(\vb{F}\)
4.2 Back
- \(\vb{F} = \grad{f}\)
- Choose a path from origin and finish at \((x_1, y_1)\)
- \({\displaystyle \int_{0,0}^{x_1,y_1} \vb{F} \dd{\vb{r}} = f(x_1, y_1) - f(0, 0)}\)
- \({\displaystyle f(x,y) = \int_{(0,0)}^{(x_1,y_1)} \vb{F} \dd{r} + c}\)
- where \(c\) is an arbitrary constant of integration where \(c = f(0,0)\)
5 How can we get the potential function using antiderivatives?
5.1 Front
How can we get the potential function using antiderivatives?
\(\vb{F}\), for example \(\vb{F} = \ev{x+y^2, 2xy + 3y^2}\)
5.2 Back
- \(\vb{F} = \grad{f} \implies M \vu{i} + N \vu{j} = f_x \vu{i} + f_y \vu{j}\)
- Get a partial derivative for example \(f_x\)
- \(\pdv{f}{x} = x + y^2\) (Hold \(y\) fixed, integrate with respect to \(x\))
- \({\displaystyle f = \frac{1}{2} x^2 + y^2x + g(y)}\), where \(g(y)\) is an arbitrary function of \(y\)
- Find \(g(y)\) using
- \(\pdv{f}{y} = 2yx + g’(y)\) by previous calculation of \(f\)
- \(\pdv{f}{y} = 2xy + 3y^2\) from \(\vb{F}\)
- Comparing these 2 expressions, \(g’(y) = 3y^2 \implies g(y) = y^3 + c\)
- Putting all together, \({\displaystyle f(x,y) = \frac{1}{2} x^2 + y^2x + y^3 + c}\)
6 What is the exactness criterion?
6.1 Front
What is the exactness criterion?
\(\vb{F}\)
6.2 Back
- \(\vb{F} = M \dd{x} + N \dd{y}\) where \(M,N\) are continuously differentiable in a region \(D\) of the plane
- \(M \dd{x} + N \dd{y}\) is exact differential of \(f\) which \(\implies M_y = N_x\)
- if \(D\) is the whole \(xy\text{-plane}\), \(M_y = N_x \implies M \dd{x} + N \dd{y}\) is exact
7 What can we say if the expression \(M \dd{x} + N \dd{y}\) is exact?
7.1 Front
What can we say if the expression $M \dd{x} + N \dd{y}$ is exact?
In a region \(D\) where \(M\) and \(N\) are defined
7.2 Back
This expression is exact if the total differential of some function \(f(x,y)\) in this region is \(\dd{f} = M \dd{x} + N \dd{y}\)
This implies that \(\vb{F} = M \dd{x} + N \dd{y}\) is a gradient of \(f\) (\(\grad{f}\)).
If \(M,N\) are continuously differentiable for all \(xy\text{-plane}\), we can use the criterion \(M_y = N_x\) and check if \(\vb{F}\) is a gradient field