1 Chalkboard
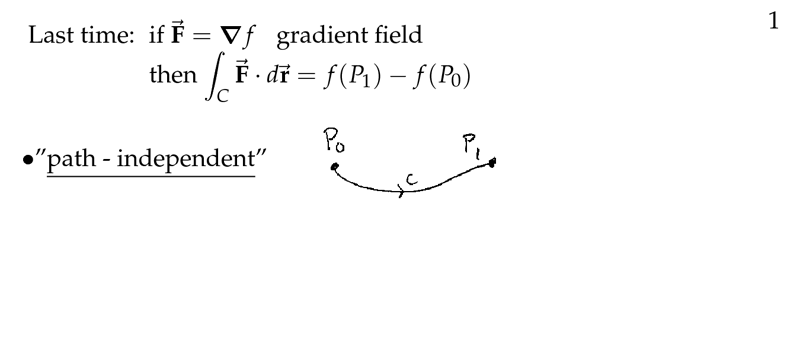
Figure 1: Recall FCT for line integral with gradient fields

Figure 2: Meaning of conservative field
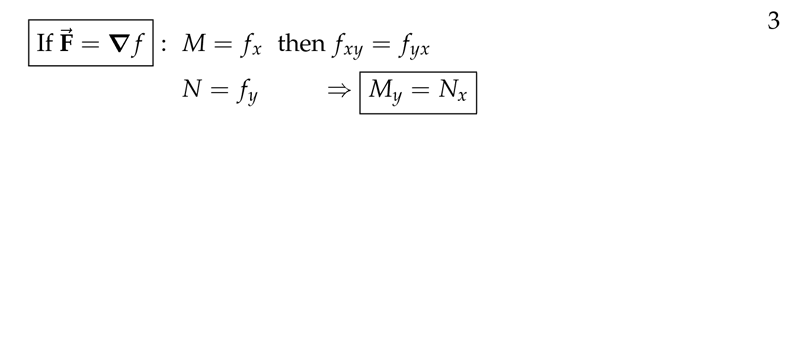
Figure 3: How to know if vector fields is a gradient field
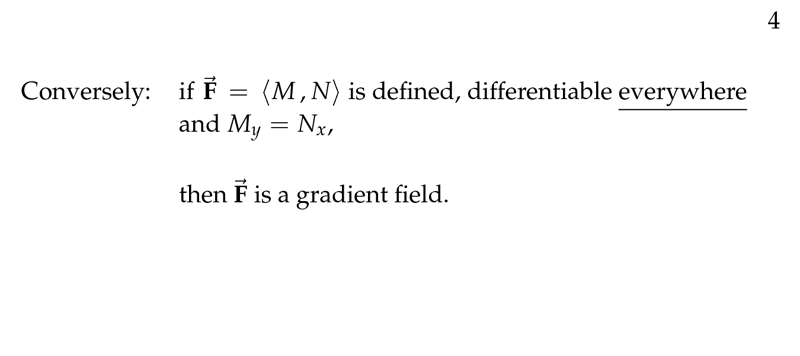
Figure 4: Test for gradient field
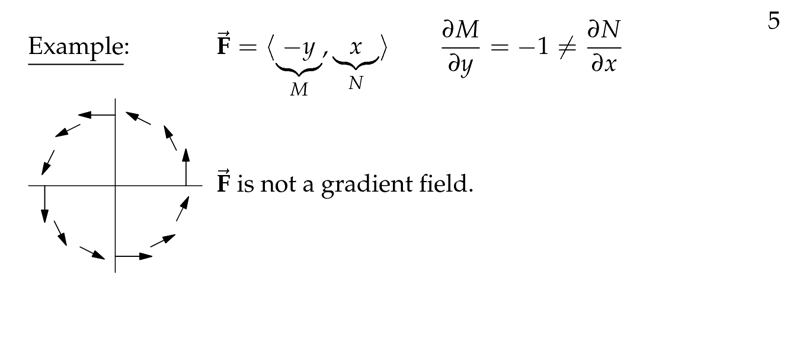
Figure 5: Example of non gradient field
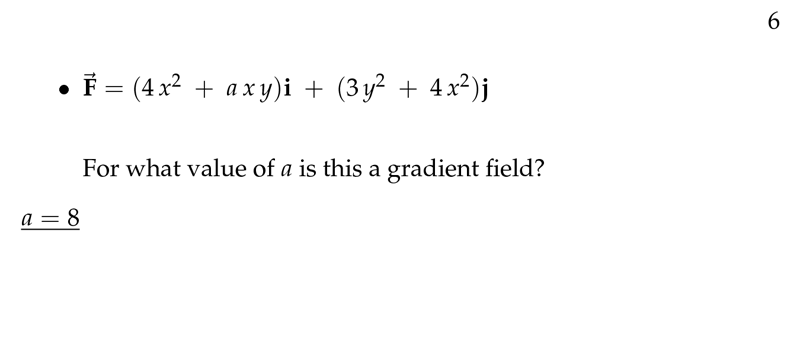
Figure 6: For which values of \(a\) \(\vb{F}\) is a gradient field?

Figure 7: Example answer
2 How can we say that a given \(\vb{F}\) is a conservative field?
2.1 Front
How can we say that a given $\vb{F}$ is a conservative field?
Let \(\vb{F} = M \vu{i} + N \vu{j}\). And using curl
2.2 Back
- \(\vb{F}\) is continuously differentiable in a region \(D\)
- \(M = f_x\)
- \(N = f_y\)
- In \(D\), \(\vb{F} = \grad{f}\) for some \(f(x,y) \implies M_y = N_x\)
- \(M_y = f_{xy}\)
- \(N_x = f_{yx}\)
Using two-dimensional curl of \(\vb{F}\)
\(\text{curl} \vb{F} = \grad{f} = N_x - M_y = 0\)
If \(\text{curl} \vb{F} = 0\), then \(\vb{F}\) is a gradient field
3 Show that this vector field is not conservative
3.1 Front
Show that this vector field is not conservative
\({\displaystyle \vb{F} = \frac{-y \vu{i} + x \vu{j}}{x^2 + y^2}}\)
3.2 Back
You can not apply the conversion criteria, and check that \(\text{curl} \vb{F} = 0\) because \(\vb{F}\) is not defined at origin \((0,0)\)
If you check it, \({\displaystyle M_y = N_x = \frac{y^2 - x^2}{(x^2 + y^2)^2}}\)
To show that \(\vb{F}\) is not conservative, you need to compute \({\displaystyle \oint_C \frac{-y}{x^2 + y^2} \dd{x} + \frac{x}{x^2 + y^2} \dd{y}}\). Let \(C\) unit circle for example (you can get any closed curve). In this case, is \(2 \pi \neq 0\)
4 How can we show a exact differential?
4.1 Front
How can we show a exact differential?
For example, show that \((xe^x + y)\dd{x} + x \dd{y}\) is exact
4.2 Back
- \(M \dd{x} + N \dd{y}\) is exact differential if and only if \(\vb{F}\) is a gradient field
- To show \(\vb{F}\) is a gradient field, we must show that \(\vb{F}\) is continuously differentiable and \(M_y = N_x\) for all \(x,y\)
- \(\vb{F}\) is continuously differentiable for all \(x,y\) by inspection
- \(M_y = N_x = 1\)
- Show is exact
5 What is the equation of a two dimensional curl of \(\vb{F}\)?
5.1 Front
What is the equation of a two dimensional curl of $\vb{F}$?
5.2 Back
- \(\vb{F} = M \vu{i} + N \vu{j}\)
- \(\text{curl} \vb{F} = N_x - M_y\), is a scalar function