1 Chalkboard

Figure 1: Gradient fields in physics

Figure 2: Meaning of conservativeness

Figure 3: Equivalent properties I

Figure 4: Equivalent properties II
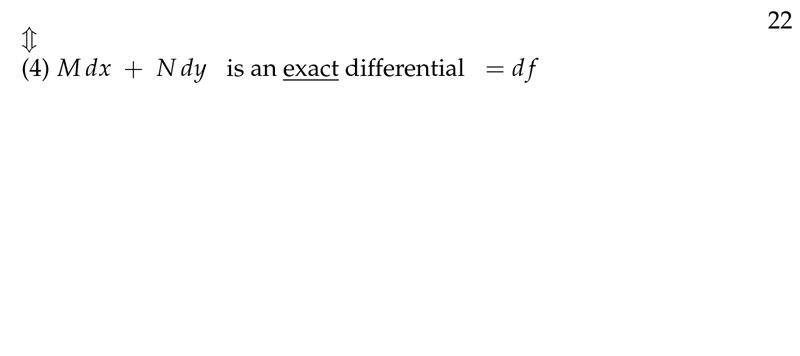
Figure 5: Equivalent properties III
2 How can we proof that path independence is equivalent to conservative?
2.1 Front
How can we proof that path independence is equivalent to conservative?
\(\vb{F}\) is a vector field and \(C\) any curve
2.2 Back
\(\vb{F} = \grad{f}\) is a gradient field
There are 2 method to show up
- Path independence \(\implies\) the line integral around any closed
path is 0
- Since the starting point is the same as finish point we get \({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = f(P_1) - f(P_0) = 0}\)
- The line integral around any closed path is 0 \(\implies\) path
independence
- Assume \({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = 0}\) for any closed curve
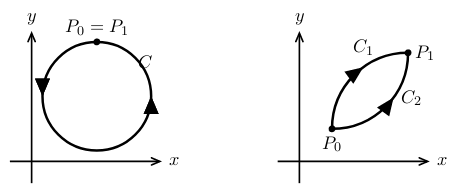
- If \(C_1\) and \(C_2\) are both paths between \(P_0\) and \(P_1\), then \(C_1 - C_2\) is a closed path
- \({\displaystyle \oint_{C_1 - C_2} \vb{F} \dd{r} = \int_{C_1}
\vb{F} - \int_{C_2} \vb{F} \dd{\vb{r}} = 0}\)
- \({\displaystyle \int_{C_1} \vb{F} \dd{\vb{r}} = \int_{C_2} \vb{F} \dd{\vb{r}}}\) (Show path independence)
3 What happens when line integral of close path is not 0?
3.1 Front
What happens when line integral of close path is not 0?
\({\displaystyle \oint_C \vb{F} \cdot \vu{T} \dd{s} \neq 0}\)
Example: \(\vb{F} = \ev{-y, x}\)
3.2 Back
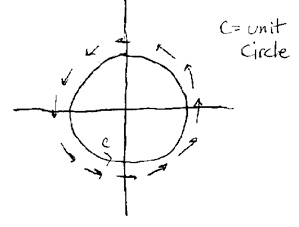
\(\vb{F} \cdot \vu{T}= \abs{\vb{F} = 1}\)
- \(\vb{F}\) is not conservative
- \(\vb{F}\) is not a gradient field
- \(\vb{F}\) is not path independent
4 What does mean this equation in physics?
4.1 Front
What does mean this equation in physics?
\(\vb{F} = \grad{f}\)
4.2 Back
\(\vb{F}\) is gradient of potential \(f\). In reality, it’s negative but in mathematics isn’t.
5 What does mean work of \(\vb{F}\) in physics?
5.1 Front
What does mean work of $\vb{F}$ in physics?
5.2 Back
It the change in value of potential
e.g. gravitational field, electric field vs. gravitational/electric potential
6 What means conservative field?
6.1 Front
What means conservative field?
6.2 Back
No energy can be extracted from the field “for free”, total energy is conserved
7 What implies that a field is conservative?
7.1 Front
What implies that a field is conservative?
7.2 Back
- \({\displaystyle \oint_C \vb{F} \dd{\vb{r}} = 0}\) along all closed curves \(C\)
- \({\displaystyle \int_C \vb{F} \dd{\vb{r}}}\) is path independent
- \(\vb{F}\) is a gradient field \(\vb{F} = \grad{f} = \ev{f_x,f_y}\)
- \(\leftarrow\) Is fundamental theorem
- \(\rightarrow\) is how we find potential
- \(M \dd{x} + N \dd{y}\) is an exact differential \(= \dd{f}\)
8 How can you say that \(\vb{F}\) is conservative?
8.1 Front
How can you say that $\vb{F}$ is conservative?
Write equivalent equations
8.2 Back
\(\vb{F} = \grad{f} \Leftrightarrow \int_P^Q \vb{F} \dd{\vb{r}}\) (is path independence) \(\Leftrightarrow \oint_C \vb{F} \dd{\vb{r}} = 0\) (for any closed \(C\))
9 What does mean that a function is continuously differentiable?
9.1 Front
What does mean that a function is continuously differentiable?
9.2 Back
All partial derivatives exist and are continuous